用数学的眼光看世界

李玲珠

【摘 要】作为近代数学三大难题之一的“四色猜想”，体现了数学家以严谨的态度挑战未知的探究精神。文章以“四色猜想”为例，设计拓展教学方案，引导学生用数学的眼光探索、发现数学中的奥秘，培养学生初步发现问题、提出问题、分析问题、解决问题的能力。

【关键词】四色猜想;教学设计;数学教学;拓展教学

如果要把地图上任意相邻的两个地区区分开来，最少需要几种颜色？

经过漫长的探索，数学家提出了“四色猜想”，即最多用四种颜色（不相邻的区域可以涂同种颜色）就能区分出地图上任意两个相邻的区域（相邻区域的边界是直线或曲线，不能是一个点）。

“四色猜想”最初由莫比乌斯和古思里提出，之后吸引了许多数学家的目光。哈密顿为之冥思苦想13年而不得其果[1]，闵可夫斯基一次次地尝试，又一次次失败……无数数学家为之奉献一生，却仍无法得出最终的答案。就其本身而言，四色猜想并无太大的实用价值，人们完全可以用四种或者更多种颜色来区分各地区。但作为一个数学问题，它体现了人们对未知的探索态度，反映了数学家敢于迎接挑战，用数学的眼光探索问题、发现真理的理性精神。

这种态度和精神与《义务教育数学课程标准（2011年版）》（以下简称《课程标准》）所要求的用

数学的思维方式进行思考，增强发现和提出问题的能力、分析和解决问题的能力不谋而合[2]。在学生层面，《课程标准》提倡学生自己发现和提出问题，鼓励学生归纳、概括和猜想规律。在教师层面，《课程标准》同样鼓励教师开发利用社会资源，以拓展教育的方式帮助学生体会数学的价值，同时促进教师的专业成长。那么，什么样的拓展知识适合小学阶段的学生？这些知识又该如何呈现呢？

就低年级学生而言，他们更喜欢易于理解、可动手操作的教学方式。低年级学生理解力较弱，在一节课中的专注力也有限，所以找一个容易理解、吸引学生注意力的知识很有必要。“四色猜想”作为小学数学的拓展课程完全符合上述要求，学生能够听懂四色猜想的定义，而且可以通过涂色的方式来验证猜想。当然，四色猜想更重要的目的是在证明猜想的过程中培养学生发现、推理、概括等能力，弥补学生在平时课堂中没时间探索的遗憾，也能为落实学生的主体地位提供很好的机会。

（一）以謎为引，揭示主题

师：同学们，老师今天带来了一个谜语，想请你们猜一猜。一张画儿墙上挂，有的小来有的大，小的容纳几个县，大的可包全天下。同学们知道是什么吗？

生（齐声）：地图！

师：真厉害！那你们见过哪些地图呢？

生1：我见过中国地图、世界地图、XX市的地图……

师：看来大家都见过很多地图呢！今天我们一起来探究区域图的秘密。

（二）画区成域，循序渐进

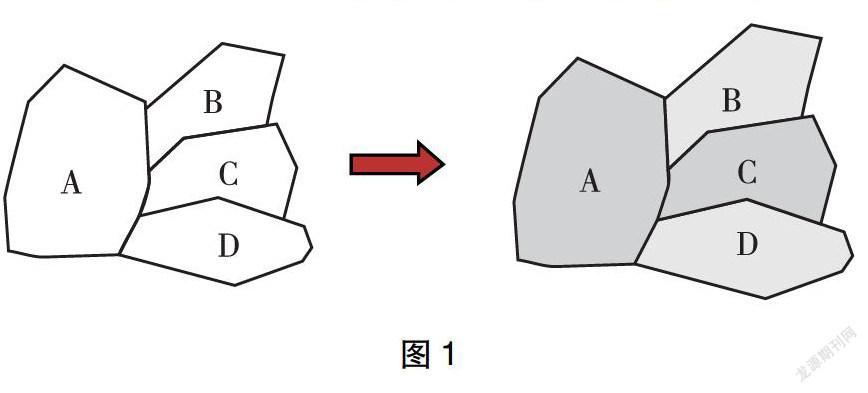
1.探索4块区域涂色

师：如果相邻区域不能涂同种颜色，那么下面这几块区域（见图1）最少需要几种颜色？

生2：通过涂色可知，这几块区域最少需要三种颜色。

师：假如地图里的区域数增多了，需要的颜色种数会发生什么变化？

生3：图里区域数增多，需要的颜色种数也会增多。

学生通过主观判断，认为区域数越多，需要的颜色种数也会变多。这正是数学发展道路上的第一步——猜想，也是数学历史进程中一个非常重要的步骤。不管学生的猜想是对还是错，教师都应该从学生的角度出发，和学生一起进行下一步的探究。

2.验证7块区域涂色

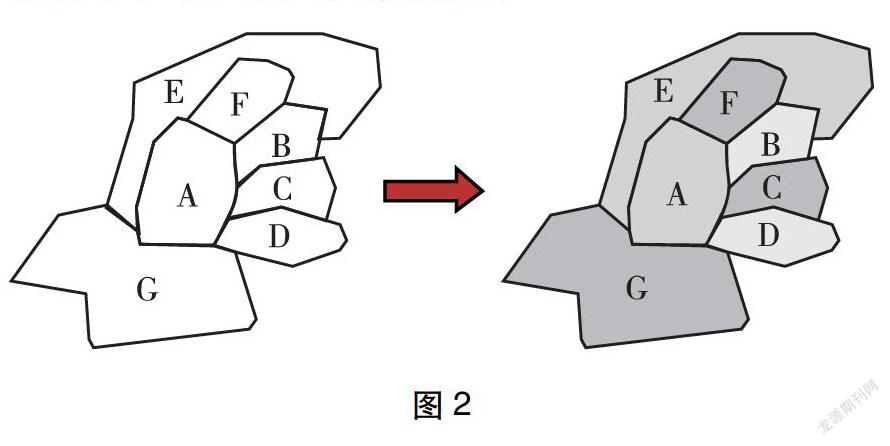
当区域数增加到7块时（见图2），在相同的条件下，最少需要几种颜色？

学生通过涂色可知，完成这幅图最少需要四种颜色。

师：回到刚才的问题，随着区域数的增多，所需要的颜色种数会发生什么变化？

生4：随着区域数增多，颜色的种数也会增多。

从4块区域到7块区域，随着区域数增多，需要颜色的种数的确增多了（增加了1种），这似乎验证了学生的猜想，为学生进行下一步探究增添了信心。

3.验证10块区域涂色

当区域数增加到10块时（见图3），学生继续涂色验证之前的猜想。

学生通过继续涂色可知，完成这幅图最少只要四种颜色。

师：刚才我们说区域数越多，需要的颜色种数就会越多，这幅图却不是。如此，我们的猜想并不正确。那么区域数越多，需要的颜色种数到底会发生什么样的变化呢？

生5：也许颜色种数到一定数量后就会保持不变？

师：那我们再增加区域数量，看看是否会得到我们想要的结果。

4.验证13块区域涂色

当区域数增加到13块时（见图4），学生继续涂色探究。

学生经过教师的引导和他们之间的尝试、讨论发现，完成这幅区域图最少只要四种颜色。

生6：虽然区域数量增多了，但最后也只用4种颜色。也就是说，区域数量再多，4种颜色也足够将其区别出来！

师：同学们似乎发现了一个新秘密，但真的是这样吗？我们还得继续验证。（出示有30个区域的图形）

5.用多块区域图验证“四色猜想”

通过师生合作，学生发现完成一幅有30个区域的图形最多只要4种颜色。这就进一步证明了学生的猜想：最多只需要4种颜色就能将图上的所有区域区分开来。

师：那么如果我们用更多块区域的图还会得出这个结论吗？

生（齐生）：会！

历史上每一个新发现都是科学家经过无数次实验，从不断的失败与修正中得来的。所以学生在面临数学问题时也应遵循这样的过程：提出猜想→验证→修正→继续推理与验证……直到一个“新的”理论产生。更多块区域的图的展示是对学生发现的一种肯定，也是对“四色猜想”的肯定。他们通过自己的努力发现了新知识，这也是数学赠与他们的礼物。在教学的过程中，教师要时常让学生感受到数学是有逻辑的，是需要反复论证的。只有这样，学生才能养成思考的习惯，才可能用数学的眼光去看待问题、解决问题。张奠宙先生提倡，对待数学问题“不仅要有冰冷的美丽，还要有火热的思考”[3]，只有经过反复的、火热的思考，才能得出真正的答案。同样，只有让学生养成对数学的兴趣，才能对今后遇到的数学问题进行积极思考。

在小学二年级的学生中进行了“四色猜想”的拓展课初尝试后，笔者有了一些发现。

1.学生喜欢并且能够以探索的方式处理数学问题。在拓展课上，二年级学生表示非常喜欢这种涂色的数学课，并认为“四色猜想”的探索过程充满了乐趣。从猜想“区域数越多，需要的颜色种数越多”，到“区域数增多，需要的颜色种数没有增多”，再到确认“区域数再多，需要的颜色种数只要4种即可”，最后得出“四色猜想”。學生的每一步猜想都是他们主动探索出来的。

2.区域数增多后学生涂色的正确率下降，但大部分学生仍能正确涂色。从涂色结果来看（见表1），学生完成4块、7块、10块区域涂色的正确率分别是92.5、72.5、65，正确率依次下降。但从整体来看，大部分学生能够理解“四色猜想”的内涵，并且能够做出正确的涂色。

3.学生的主要问题在于“多涂”和“相邻区域涂同种颜色”。

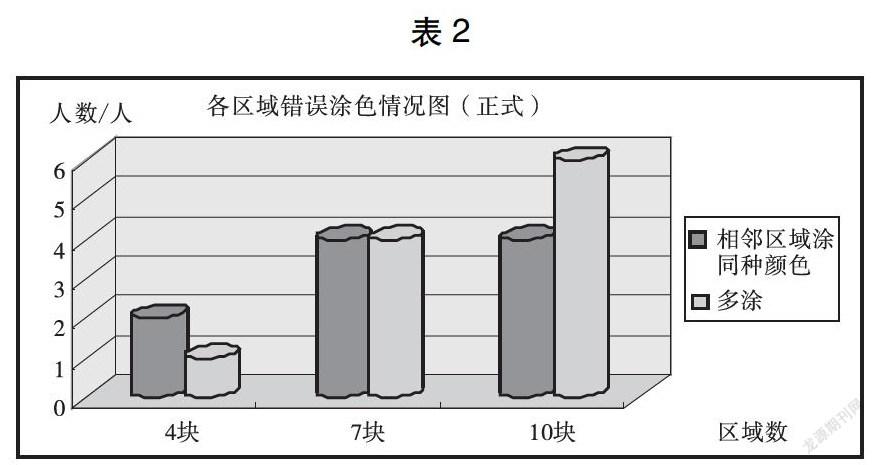
从学生的错误涂色情况可知（见表2），随着区域数增多，学生的主要问题在于“多涂”。

从4块区域的涂错情况来看，学生主要错在没有满足“相邻区域不能涂同种颜色”这一条件上。从7块区域的涂错情况来看，“相邻区域涂同种颜色”与“多涂”的犯错人数同样多。从10块区域的涂错情况来看，“多涂”的人数超过了“相邻区域涂同种颜色”的人数。

1.学生对数学的探索过程充满自信并且乐于探索。从学生的行动与讨论中可知，学生对这类探索课是感兴趣的。虽然最开始的猜想是错的，但经过后期的验证活动让学生对自己产生了更多的自信。研究表明，此阶段的学生正处于直观层次到描述、分析层次的过渡阶段，他们能够简单地进行分析与比较，但还不会做严格的推导、论证[4]，所以错误猜想的产生也符合该阶段学生的认知。

整节课下来，所有的猜想与结论（包括正确的、不正确的结论）都是学生主动提出并探索的，教师只起到引导作用。从课堂整体氛围来看，他们对数学探索与发现过程充满了乐趣与自信。

2.“四色猜想”对二年级学生的教学是可行的。从涂色的结果来看，大部分学生都能够正确完成涂色任务，说明本次“四色猜想”在二年级的数学尝试是成功的，在同年级进行推广也具有可行性。

3.多区域的涂色需要教师进一步引导及团队合作。多区域图建议采用团队合作的方式，也可以由师生共同完成。因为当涉及的区域较多时，学生涂色的正确率会降低，所耗时间也会较长，所以通过团队合作或师生共同合作，是一种比较高效的办法。

参考文献：

[1]朱立明，马玉鹏.基于新课标的学生数学价值感悟研究[J].数学教育学报，2014（5）：33-35.

[2]中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

[3]张奠宙，宋乃庆.数学教育概论（第二版）[M].北京：高等教育出版社，2009.

[4]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.