把握教学细节，成就精彩课堂

仇素

摘要：教学细节是指发生在课堂教学中师生间的话语、行为，以及交互作用的各种细微环节。教师正是通过对众多教学细节的演绎而将其转化为深刻影响学生思想的可接受的力量。以《因数与倍数》一课为例，阐述教学细节的把握：理解教材，精心预设;捕捉生成，有效处理。

关键词：教学细节因数与倍数教材理解预设生成

教学细节是指发生在课堂教学中师生间的话语、行为，以及交互作用的各种细微环节。教学细节是外显的教学行为的最小单位，它表现为多样的形式和复杂的结构。教学细节不大，它只是课堂的一个极小的缩影;教学细节不小，它就像透视教学的放大镜、多棱镜，能以小见大地折射出教师的教育理念、教育智慧。教师正是通过对众多教学细节的演绎而将其转化为深刻影响学生思想的可接受的力量。本文以苏教版小学数学五年级下册《因数与倍数》一课为例，闡述教学细节的把握。

一、理解教材，精心预设

“凡事预则立，不预则废。”精彩的生成离不开教师的精心预设。有些细节表面上是信手拈来、即兴所得，实质上是匠心独运、蓄意安排的。只有注重了细节预设，才能在课堂上从容应对，把握课堂走向。而这首先是对教材编写意图的深刻理解。

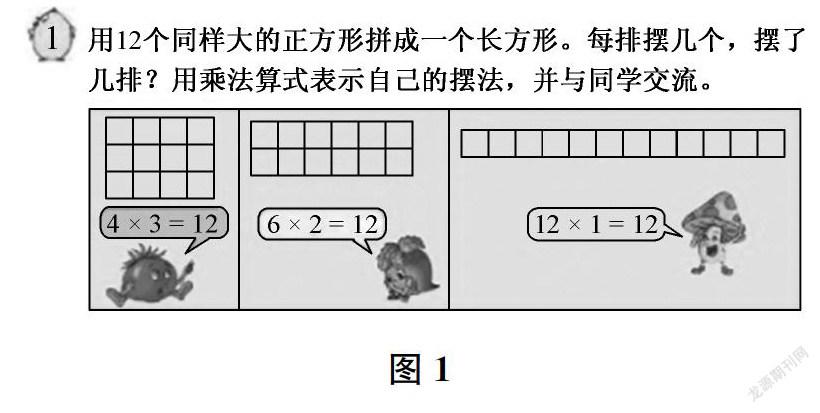
在《因数与倍数》一课的备课过程中，一开始，我认为教材例1（如图1）用12个小正方形摆长方形的编写意图就是引出三个乘法算式，操作的意义不是很大，直接引入算式倒还节省时间。

于是我有了如下的教学设想——

师（出示：？×？=12）说出一道积是12的整数乘法算式。

生3×4=12。

生2×6=12。

生1×12=12。

师3×4=12，所以3是12的因数，12是3的倍数。还可以怎样说？

生4是12的因数，12是4的倍数。

师你能不能用同样的方法说说另外两道算式？

……

后来通过实践、思考以及进一步研读教材，我认识到教材的编写意图是体现“数形结合”的思想——

1.体验“因”“倍”内涵。用12个相同的小正方形摆长方形，先让学生思考能摆成怎样的长方形。不管摆成什么样的长方形，12都是长和宽的倍数，长和宽都是12的因数，通过操作让学生体会因数和倍数的意义。

2.理解“因倍”关系。因数和倍数，是一种相互联系、相互依存的关系。学生在摆的时候可以获得体验，深刻理解这种关系。

3.巧妙渗透方法。在学生摆小正方形的时候，要提醒学生有序地摆，可按照每排的个数从小到大去摆。这样，对“成对找因数”和“不重复、不遗漏找因数”的方法进行了巧妙的渗透，有助于学生继续探究求一个数的因数。

基于上面的认识，我重新进行了教学设计——

（教师出示活动要求：1.用12个同样大小的正方形拼成一个长方形。2.每一种拼法每排摆几个，摆了几排？3.用乘法算式把各种拼法表示出来。学生操作后，小组交流反馈。）

师你表示的乘法算式是什么？

生4×3=12。

师（问全班）猜猜他可能是怎么摆的？

生一行摆4个，摆3行。

生6×2=12。

生一行摆6个，摆2行。

生12×1=12 。

生就摆1行，12个。

（教师根据学生回答，利用课件呈现相应的算式和摆法。）

师先看4×3=12，我们就可以说：12是4的倍数，12也是3的倍数，4和3都是12 的因数。谁来像老师这样手指着说一说？

（指名学生说。）

师剩下的这两道乘法算式，能自己先试一试吗？

（指名学生说。）

师这里有两句很特别，是哪两句啊？

生12是12的因数，12是12的倍数。

学生思考怎样摆时，一般都会把12个小正方形分成长和宽两个维度来思考：长摆几个？宽摆几排？这一借助表象进行的操作，能激活学生的形象思维，透过数学潜在的“形”与“数”的关系，思考并孕育最初的“因数与倍数”意识;避免简单的操作，引导学生再通过算式来表达是怎么摆的，引出算式与概念的鉴定。学生充分经历了“先由形到数，再由数到形”的过程，为下面研究因数与倍数的概念，由形象思维转向抽象思维打下了良好的基础，有效地实现了原有知识与新学知识之间的连接。

二、捕捉生成，有效处理

课堂生成是学生独立思考、动手实践、自主探索与合作交流的结果，是学生“此时此地”“此情此景”思想的真实反映。对生成性学习材料的把握实际上是又一个需要关注的教学细节问题，需要教师发挥教学智慧，及时进行捕捉并加以有效处理。

在《因数与倍数》一课教学的过程中，有这样的片段——

师（出示图2）观察这几个例子，你有什么发现？同桌相互交流一下。谁先来说说你的发现？

3的倍数有：3，6，9，12，15……

2的倍数有：2，4，6，8，10……

5的倍数有：5，10，15，20，25……

图2生3+2=5，6+4=10，9+6=15，12+8=20，15+10=25……

师明白他的意思吗？谁能用我们学过的知识来解释？

生3的1倍加上2的1倍等于5的1倍， 3的2倍加上2的2倍等于5的2倍……3的n倍加上2的n倍就等于5的n倍。我们可以根据乘法分配律得到这样结论：3×n+2×n=（3+2）×n=5×n。

师同学们从纵向发现了这3个数倍数之间的关系。请再仔细观察这3个数的倍数，它们有什么相同的地方？

生它们都没有最大的倍数，因为写不完。

生因为写不完，所以一个数的倍数有无数个。

生最小的倍数都是它们本身。

师同学们说得真好！我们一般就从一个数最小的倍数、最大的倍数以及它的个数这几方面研究一个数倍数的特点。请再联系这3个例子说一说一个数的倍数有什么特点。

……

这一部分教学设计的本意是让学生通过对比3个数的倍数，得出倍数的特征：有无数个，最小倍数为本身，没有最大倍数。而实际教学中，学生生成了别样的精彩——根据乘法分配律得到了结论：3×n+2×n=（3+2）×n=5×n。学生的理解是非常有见地的，但不是本节课的主旨。如果教师生硬地把教学过程掰回正轨——“这是一个数倍数的特征吗？”，无疑会把这富有探究味的学习问题给扼杀了，同时被扼杀的还有学生的探究精神、创新精神和学习数学的热情。这里，教师先肯定了学生的生成，又通过“纵向”的标签引导学生顺势思考“横向”的倍数特征，无疑体现了教师对于教学细节的正确把握——既认可了学生的生成，保持了学生探究和创新的热情，也完美引导学生得出了倍数的特征，纠正了学生的偏离。

把握教学细节，改变课堂教学行为，让教学细节成为教学活动的亮点，就能使看似平常的课堂有滋有味，使看似简单的课堂深刻、丰满。我们期待在把握教学细节的过程中，使学生真正成为学习的主人，使数学学习的过程成为学生享受快乐的过程。

参考文献：

[1] 陆婷.教学细节的有效处理——从预设与生成两个维度[J].教育研究与评论（小学教育教学），2019（4）.