紧急状态人口疏散算法仿真研究

周圆

摘要：当前紧急状态下疏散人群已经成为一个很重要的工作。针对疏散方案设计问题建立出口模型，分析疏散人员离开出口时的状态，并基于广度优先搜索（ BFS）的思想，利用元胞自动机模型，深入仿真每个逃离者行为，发现疏散的第一个瓶颈是出口处的流量。建立了一层多出口的面积模型，并基于“类气球”模型使用人流树的并行生长算法进行仿真;对算法进行了复杂度分析，对上述模型进行了优化，讨论了模型的优缺点，使模型设计适用于最接近现实生活中的多楼层情形。

关键词：紧急疏散策略;元胞自动机;广度优先搜索算法;数学建模

中图分类号：TU998.1

文献标识码：A

DOI： 10.15913/j.cnki.kjycx.2019.08.005

1 简介

1.1 问题背景

当前各种突发事件可能会影响人们的安全，让人们远离危险成为当今时代的一个棘手问题，尤其是在旅游景点。本文将针对某博物馆具体情况，研究逃生过程中潜在的瓶颈，并制作一系列模型来帮助设计疏散方案。

1.2 基本情况介绍

在本文中建立了出口模型和广度优先搜索来分析基本问题，利用元胞自动机模型和“类气球”模型，计算出一层的疏散方案，并以某博物馆为背景进行了仿真实验。本文考虑多楼层情况，对模型进行优化，并根据某博物馆具体情况进行了仿真。我们考虑了多种复杂的因素，让模型更加真实，并找出两个瓶颈之间牵制的关系。

2 假设

假设1：每天参观的人数是随机的。

假设2：游客参观哪里是随机的。

假设3：每天游客类型是随机的。

假设4：所以参观者在逃离时的参数是相同的。

3 基本模型

3.1 逃离模型

3.1.1 符号定义

D：出口宽度。

d：不同国家人的平均肩宽。

N：参观者总数。

v：人群的撤离速度。

l：人与人之间的平均距离。

3.1.2 模型

假设一个出口可让四个人同时通过：

假设相邻参观者之间的水平间距为0.1 m，同时可以通

3.2 深度优先搜索（BFS）[2]

深度優先搜索（ BFS）是一种遍历或搜索树或图数据结构的算法。它从树根开始，在进入下一个深度级别的节点之前，研究当前深度的所有邻居节点。这个算法将在元胞自动机和“类气球”模型中使用。

4 一层楼情形

4.1 一个出口情形

假设建筑物只有一层楼，且仅有一个出口。为了更加深入地研究每位逃离者的行为，本文使用元胞自动机模型。

4.1.1 元胞自动机模型

从统计的角度来看，当样本量足够大、时间足够长时，展厅各个区域的参观人数应该是相等的。因此，本文将整个展区平均划分为多个单元，在本文中我们将其称为“元胞”进行研究，利用元胞自动机模型模拟参观者的疏散过程。

元胞自动机的规则如下。

4.1.1.3 决定下一步的移动

对于每个元胞，它周围有8个元胞，这意味着它下一步可以从这8个方向中选择一个走。根据Moore nei曲borhood'scellular neighborhood style，每一个细胞，在选择下一个状态的方向时，每次都会选择最小的系数的方向。如果元胞当前位置的风险系数都小于周围8个元胞，逃离者则会选择在下一步不移动。

4.1.1.4 停止

元胞系统将在所有元胞都离开系统时停止更新，此时建筑物内没有游客，即逃离结束。

4.1.2 仿真

通过MATLAB软件对此情况进行仿真，得到不同博物馆内不同人数撤退时所需时间的统计模型，如图1所示。

从图1可以发现，在开始的时候，图线是非常平滑的，这意味着出口足够大，可以让游客快速离开。当游客超过500人时，系统就需要花费更多的等待时间来让所有人逃离。

4.2 三个出口情况

4.2.1 面积模型

4.2.1.1 假设

vl，v2，v3分别为三个出口的流速。

4.2.1.2 模型

本文先从方形展厅开始研究，方形展厅如图2所示。

图2中展示了各出口流速相同时的面积划分方法。由于流速不同，每个出口的流量应与流速成正比。由于三个出口的速度分别为v1，v2，v3，所以每个出口的流量之比应为v1：v2：v3，也就是每个出口的游客人数之比。在此基础上，我们将每一层的展览面积按上述比例划分为三个部分。这样，我们就可以确保三个出口同时开始和结束。

4.2.2 元胞自动机模型

规则同上。

4.2.3 “类气球”模型

对于一个博物馆系统来讲，当它满员时，让里面的所有人快速撤离，就相当于让外面的所有人快速进入并填满整个系统。在此基础上，我们将系统等价于一个盒子，出口等价于盒子的开口处（本文以4个出口为例）。然后，我们把人进入系统这个过程，类比于“等人数”空气进入气球。下面，我们将详细介绍气球系统。

4.2.3.1 鼓入空气

这个系统的第一步是根据出口的速度，让空气通过开口进入盒子。显然，随着时间的推移，一些气球会在生长点相互碰撞。当这种情况发生时，它们将平等地竞争彼此的空间，以确保自身的增长。

4.2.3.2 重要函数

上述规则将导致气球在一个方向无限膨胀，而在另一个方向的气球将被限制在一个条状内。

4.2.4 博物馆内的模拟

使用上述三种模型，借助C语言编程，我们可以得到博物馆的分区图，如图3所示。

4.3 算法细节

4.3.1 人流树的生长过程

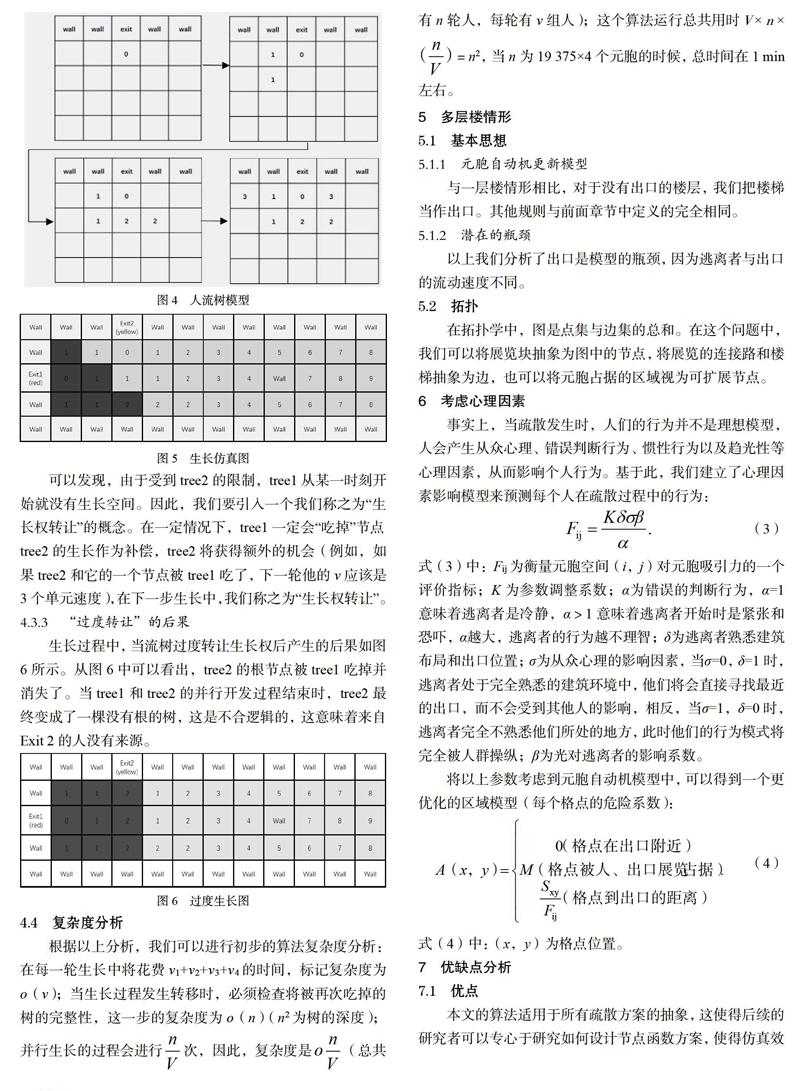
人流树模型如图4所示。

确定流速为v（图4中以v=2为例）;选择exit作为根节点，并将其值标记为“0”。在下一轮中，将其向8个方向展开，并将这8个节点放人一个等待队列中。根据先来先服务的队列规则，从队列中选择V个节点，并将这些节点标记为“1”，类似于广度优先搜索（ BFS）的过程。

4.3.2 生长过程中的问题

我们用以下方式標记树：出口α是树α，也就是说出口α是气球的α口，α是出口的标记。如果我们不设置任何限制，将会出现非常不利的现象，如图5所示。

可以发现，由于受到tree2的限制，treel从某一时刻开始就没有生长空间。因此，我们要引入一个我们称之为“生长权转让”的概念。在一定情况下，treel -定会“吃掉”节点tree2的生长作为补偿，tree2将获得额外的机会（例如，如果tree2和它的一个节点被treel吃了，下一轮他的v应该是3个单元速度），在下一步生长中，我们称之为“生长权转让”。

4.3.3 “过度转让”的后果

生长过程中，当流树过度转让生长权后产生的后果如图6所示。从图6中可以看出，tree2的根节点被treel吃掉并消失了。当treel和tree2的并行开发过程结束时，tree2最终变成了一棵没有根的树，这是不合逻辑的，这意味着来自Exit 2的人没有来源。

4.4 复杂度分析

根据以上分析，我们可以进行初步的算法复杂度分析：在每一轮生长中将花费v1+v2+v3+v4的时间，标记复杂度为o（v）;当生长过程发生转移时，必须检查将被再次吃掉的树的完整性，这一步的复杂度为o（n）（n2为树的深度）;并行生长的过程会进行n/V次，因此，复杂度是o n/V（总共

有n轮人，每轮有v组人）;这个算法运行总共用时Vx nx（n/V）=n2，当”为19 375x4个元胞的时候，总时间在1 min左右。

5 多层楼情形

5.1 基本思想

5.1.1 元胞自动机更新模型

与一层楼情形相比，对于没有出口的楼层，我们把楼梯当作出口。其他规则与前面章节中定义的完全相同。

5.1.2 潜在的瓶颈

以上我们分析了出口是模型的瓶颈，因为逃离者与出口的流动速度不同。

5.2 拓扑

在拓扑学中，图是点集与边集的总和。在这个问题中，我们可以将展览块抽象为图中的节点，将展览的连接路和楼梯抽象为边，也可以将元胞占据的区域视为可扩展节点。

6 考虑心理因素

事实上，当疏散发生时，人们的行为并不是理想模型，人会产生从众心理、错误判断行为、惯性行为以及趋光性等心理因素，从而影响个人行为。基于此，我们建立了心理因素影响模型来预测每个人在疏散过程中的行为：式（3）中：F_ij风为衡量元胞空间（i，j）对元胞吸引力的一个评价指标;K为参数调整系数;α为错误的判断行为，α=1意味着逃离者是冷静α>l意味着逃离者开始时是紧张和恐吓，α越大，逃离者的行为越不理智;δ为逃离者熟悉建筑布局和出口位置;σ为从众心理的影响因素，当σ=0，δ=1时，逃离者处于完全熟悉的建筑环境中，他们将会直接寻找最近的出口，而不会受到其他人的影响，相反，当σ=1，δ=0时，逃离者完全不熟悉他们所处的地方，此时他们的行为模式将完全被人群操纵;β为光对逃离者的影响系数。

将以上参数考虑到元胞自动机模型中，可以得到一个更优化的区域模型（每个格点的危险系数）：

7 优缺点分析

7.1 优点

本文的算法适用于所有疏散方案的抽象，这使得后续的研究者可以专心于研究如何设计节点函数方案，使得仿真效果更加拟合来自社会（心理学）模型所推导的疏散构造需求。

7.2缺点

本文的算法可能要运行1 nun之久，这已经超过了人类面对危险时的等待忍受极限。

8措施建议

大概每5 min，中控机房应该重新根据最新数据，运行一遍程序，以供系统重新设计疏散规划方案。

参考文献：

[1]崔喜红，李强，陈晋，等.大型公共场所人员疏散模型研究——考虑个体特性和从众行为[J].自然灾害学报，2005（6）：133-140.

[2]白雪岑.基于元胞自动机的特殊人群疏散仿真研究[C]//中国力学学会第十七届北方七省市区力学学会学术会议论文集.2018

[3]金泽人，阮欣，李越.基于元胞自动机的火灾场景行人流疏散仿真研究[J].同济大学学报（自然科学版），2018， 46（8）：1026-1034.

[4]朴勋，耿雪川.小型建筑火灾中人群智能疏散引导模拟研究[J].科技通报，2018，34（9）：238-241，248.