时变时滞奇异摄动Lurie系统的稳定性分析

孙凤琪

(吉林师范大学 数学学院, 吉林 四平 136000)

0 引 言

随着科学技术的飞速发展和人们认知能力的不断提高, 在控制领域迅速深入完善发展的今天, 研究者们不得不对比较复杂的非线性系统进行研究。Lurie系统就是一类具有典型结构特点和广泛应用背景, 能更加准确建模反映客观实际的一类非线性系统, 它能代表非线性系统的许多本质特征, 是一种形式上的反馈系统: 前馈通道和反馈通道分别是线性定常系统和满足扇形约束的非线性环节。人们可以用非线性孤立方法把一些非线性系统的非线性部分分离出来, 而形成Lurie型系统。因此, 研究Lurie系统的稳定性问题对于进一步完善系统理论, 揭示非线性系统的本质特征都有非常重要的意义[1-2]。

自绝对稳定性的概念被提出后, 绝对稳定性理论发展成为稳定性理论中的重要分支, 控制系统实现所要求的控制功能就必须是稳定的, 所以它是现代控制系统分析与设计的首要问题。近些年来, 国内外相关学者对Lurie系统的各种稳定性问题进行了广泛的研究与探讨, 也取得了很多的相关理论成果[3-4]。

文献[5-7]较早研究了复合L-K函数的存在性, 其主要思想是将原系统分解为两个低阶系统, 即降阶系统和边界层系统。在文献[6-8]中分别给出了Lurie型广义系统的强绝对稳定的定义, 以及圆判据和Popov判据。关于Lurie控制系统强绝对稳定性的局限性, 还有许多需要进一步解决的问题, 上述提及的所有结论都要求控制系统的线性时不变部分是容许的, 即正则、 稳定、 无脉冲, 且没有涉及摄动问题。目前, 对于含有不确定性的时变时滞奇异Lurie系统的稳定性研究, 在理论上虽已取得一些成果, 但对含有不确定性结构的时变时滞奇异摄动Lurie系统的研究还较少。笔者基于现有成果的理论基础上[8-10], 研究含有不确定性结构的时变时滞奇异摄动Lurie系统的稳定性问题, 主要对一般的扇形区域内的绝对稳定进行分析, 得到保守性更小的充分性判据, 通过数值算例验证所得结论的优越性和可行性, 最后提出还需进一步研究的问题。

1 相关引理

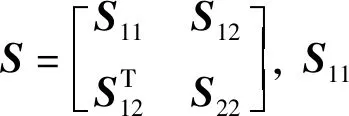
1)S<0;

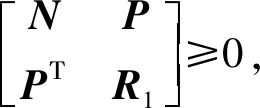
1)S1≥0;

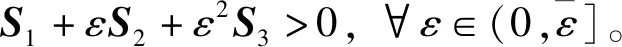
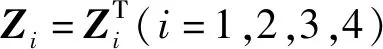
1)Z1>0;

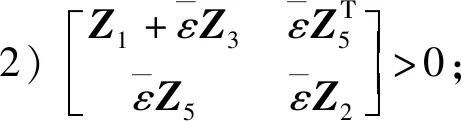
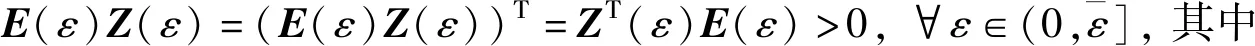
引理5[9]给定适当维数的矩阵Y,D和E, 其中Y是对称阵, 不确定函数F(t),有FΤ(t)F(t)≤I, 则Y+EF(t)D+DΤFΤ(t)EΤ<0的充要条件是, 存在一个常量η>0, 使Y+ηEEΤ+η-1DΤD<0。

2 Lurie控制系统的稳定性分析

考虑以下含不确定性的时变时滞奇异摄动Lurie控制系统

(1)

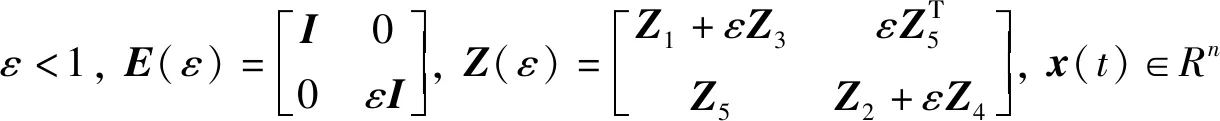
(2)

其中τ,μ为已知常量,F(t)∈Ri×j表示不确定模型的参数矩阵, 满足

FΤ(t)F(t)≤I

(3)

系统的反馈关联具有形式

w(t)=-φ(t,z(t))

(4)

其中非线性函数φ(t,z): [0,∞)×Rm→Rm属于扇形区域[V1,V2], 即

[φ(t,z)-V1z]T[φ(t,z)-V2z]≤0, ∀t≥0, ∀z∈Rm

(5)

V1和V2是已知的实矩阵, 且V=V2-V1是一个对称正定矩阵。

定义1[8]如果对所有属于扇形区域[V1,V2]的非线性函数φ(t,z), Lurie系统(1)是全局渐近稳定的, 则Lurie系统(1)称为在扇形区域[V1,V2]内绝对稳定。

注1 现有结果,τ可以取到∞[9]。

注2 条件式(2)在现有一些文献中可以被放宽[8-10], 在实际理论中被广泛应用于含有不确定性的时变时滞奇异摄动Lurie系统的分析设计中。

2.1 Lurie系统在扇形区域[0,V]的稳定性分析

非线性函数φ(t,z)属于扇形区域 [0,V], 即φ满足

φΤ(t,z)[φ(t,z)-Vz]≤0

(6)

的扇形约束条件。

2.1.1 时滞依赖的稳定性判据

Z1>0

(7)

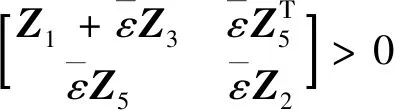
(8)

(9)

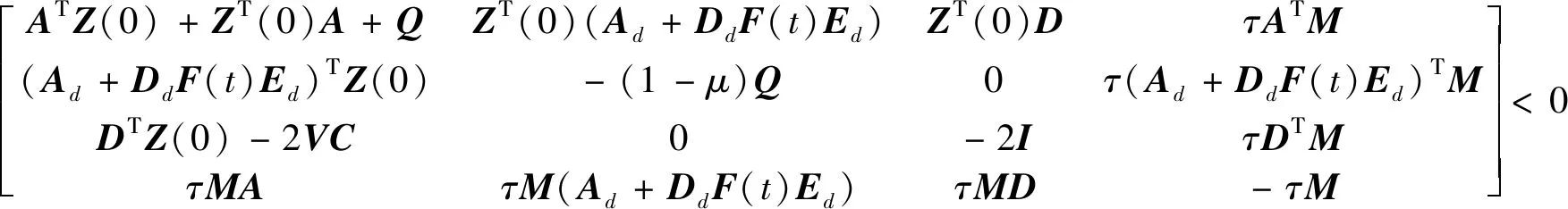
(10)

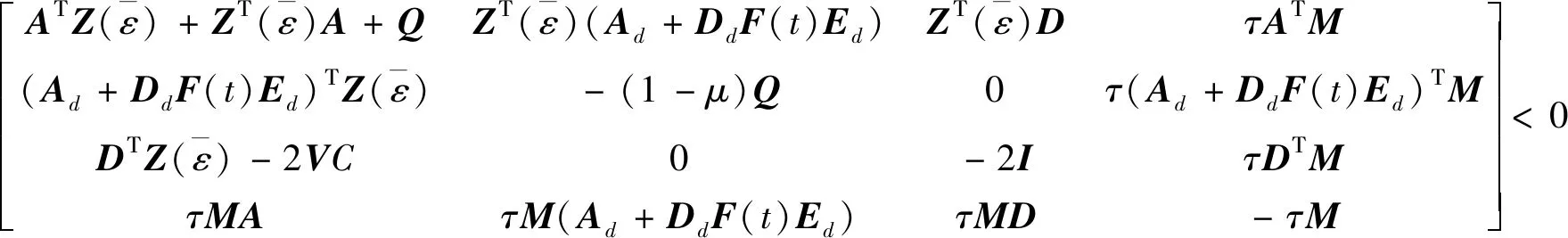
(11)

证明 定义一个二次L-K泛函V=V1+V2+V3, 其中

其中Q、M为对称正定矩阵, 即QΤ=Q>0、MΤ=M>0。

由引理4和线性矩阵不等式(7)～式(9) ,有

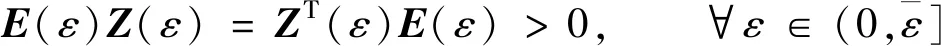
(12)

这样V就为正定的L-K泛函。

沿系统(1)的任意轨线,V1关于时间的导数

同理V2和V3关于时间的导数分别是

利用0≤2wΤ(-w-Vz), 再根据Lurie系统(1)中z(t)=Cx(t), 整理可得

其中

由于

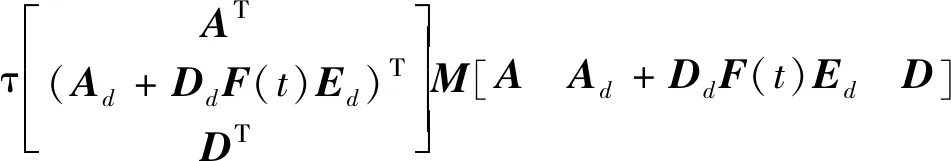
(13)

由Schur补引理, 式(13)等价于

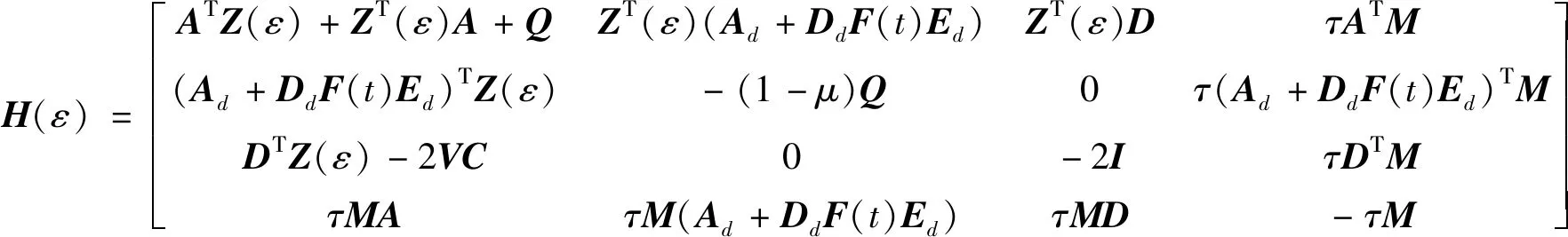
(14)

为求解定理1中的未知参数变量, 应消除式(14)中的不确定函数F(t), 由引理5知, 存在一个正常数η>0, 使

成立。由Schur补引理, 整理可得矩阵不等式对于变量η、Q、M和Z(ε)是线性的, 在式(7)～式(9)条件下, 得如下定理。

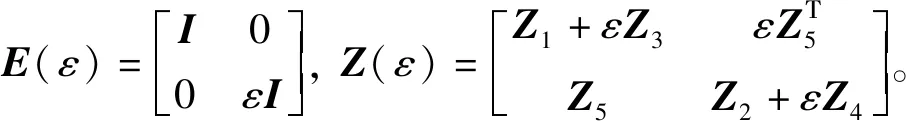
2.1.2 时滞独立的稳定性判据

证略。

2.2 Lurie系统在扇形区域[V1,V2]的稳定性分析

对非线性函数在一般扇形区域[V1,V2]中的情形, 通过应用反馈环的变换可得系统(1)在扇形区域[V1,V2]内的绝对稳定性等价于系统

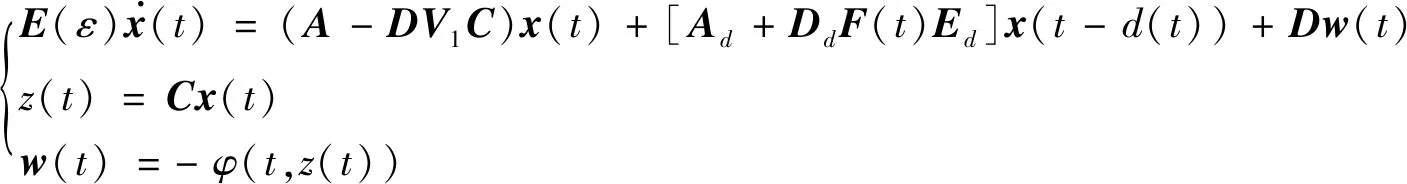
(15)

在扇形区域[0,V2-V1]内的绝对稳定性。

2.2.1 时滞依赖的稳定性判据

其中

L11(0)=(A-DV1C)ΤZ(0)+ZΤ(0)(A-DV1C)+Q

证略。

2.2.2 时滞独立的稳定性判据

证略。

3 算 例

考虑以下时变时滞奇异摄动Lurie控制系统

其中

φ(t,z)=0.25z+0.5sinz,d(t)=0.5,τ=1,μ=0.8,

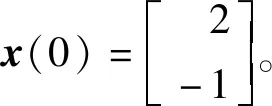
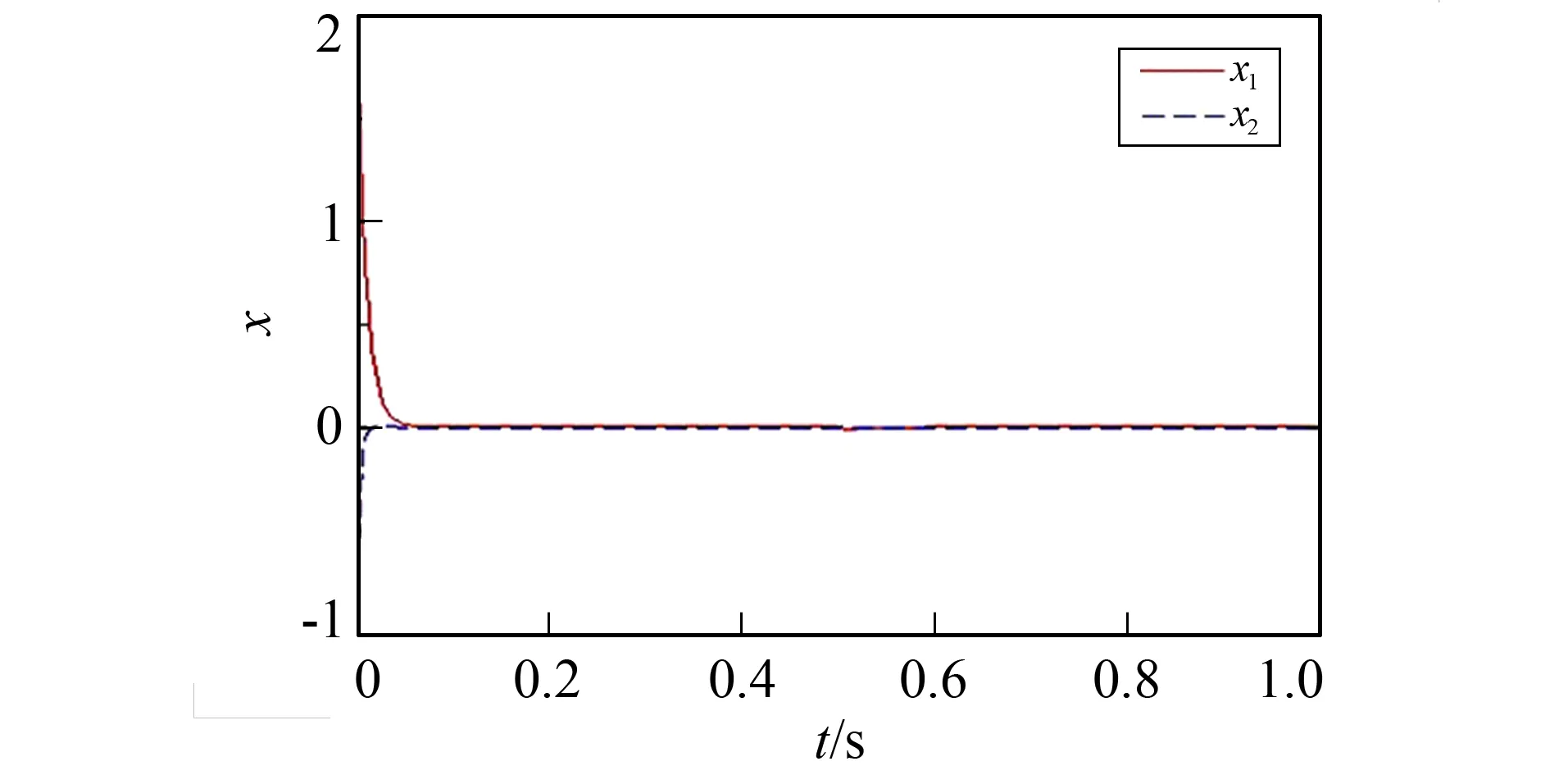
图时系统的状态响应曲线Fig.1 The state response curve of the system in

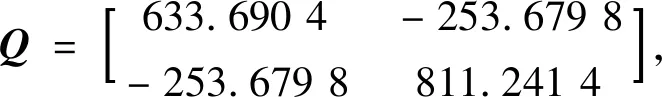
Z2=5.385 3,Z3=0.419 2,

Z4=-0.127 0,Z5=-0.252 2

因此, 根据定理2, 该系统对∀ε∈(0,0.3]是在扇形区域(0,1]内绝对稳定的。

4 结 语

笔者利用L-K稳定性理论, 构造出一种新的L-K泛函, 研究含有不确定性结构的时变时滞奇异摄动Lurie系统(1)在扇形区域[0,V]和[V1,V2]内的绝对稳定性, 得到了此Lurie系统在不同的扇形区域的时滞依赖和时滞独立的绝对稳定性充分判据, 且所有结论均以线性矩阵不等式形式给出。笔者研究了时变时滞奇异摄动鲁棒控制下的Lurie系统稳定性问题, 对非线性系统相应理论的进一步研究奠定了基础。 笔者只是相关理论的前段控制系统分析部分, 后期系统控制理论已经完成, 篇幅所限, 将在下一篇论文中给出。笔者所用到的方法和得出的结论也存在一定的局限性： 所选非线性函数φ(t,z)属于的扇形区域的不同, 最后得到的线性矩阵不等式也会有所不同； 如何定义一个新的二次L-K泛函以及如何找到新的交叉项界定方法, 有待作进一步探讨研究。