基于混合算法的点云配准方法研究

任伟建, 高梦宇, 高铭泽, 张 鹏, 刘 丹

(1. 东北石油大学 a. 电气信息工程学院； b. 黑龙江省网络化与智能控制重点实验室, 黑龙江 大庆 163318；2. 中国石油管道局工程有限公司 设计分公司, 河北 廊坊 065000； 3. 中国海洋石油集团有限公司 东方石化有限责任公司, 海南 东方 572600； 4. 中国石油天然气股份有限公司 辽河油田分公司钻采工艺研究院, 辽宁 盘锦 124010)

0 引 言

点云配准是将来自不同角度的点云数据匹配到同一坐标系的过程[1], 此过程采用了刚性变换的方法, 它是三维重建中最重要且最困难的步骤, 直接影响着三维重建的精度与效率, 在该领域中得到了诸多学者的热切关注, 同时也在三维建模、计算机视觉、逆向工程、SLAM等[2]诸多领域中有非常广泛的应用。目前, 比较主流的配准算法是迭代最近点算法, 即ICP (Iterative Closest Point) 算法, 该算法是Besl等[3]于1992年提出的, 其基本思想是通过旋转、平移使两个点集之间的距离最小。算法第1步根据计算出的不同点云间的欧氏距离进行不同点对的匹配工作; 第2步在获取已匹配点对的基础上, 求取两组点对坐标变换的参数; 第3步使用最小二乘迭代法求取目标函数, 并使结果最小直至满足设定条件。不同于基于其他特征的配准算法, 在运用ICP算法配准过程中, 点对的匹配度高, 但其仍存在一些缺点。ICP算法对初始点云的位置条件要求严苛, 收敛速度慢且易陷入局部最优。对于ICP算法的不足, 国内外研究人员对此进行了改进, Greenspan等[4]在ICP算法中引入最近邻域问题, 提高了最近点的搜索速度, 而Batlle等[5]、 Du等[6]的仿射法都只解决了部分问题, 仍存在配准精度低等问题。为提高配准的精度, 笔者引入人工萤火虫算法和粒子群算法并对其进行改进, 利用改进后的新算法对点云进行初始配准。

1995年Kennedy等[7]提出粒子群优化算法(PSO： Particle Swarm Optimization), 该算法是一种基于鸟群觅食行为的新兴智能仿生算法。由于群体中的粒子相互之间会发生规律性运动, 产生的群体性智能可作为粒子群优化算法运行的理论依据, 使其在一定区域内完成优化搜索工作。粒子群算法在拥有结构简单、 全局搜索的能力强等优势的同时, 仍会由于过早收敛使搜索结果陷于局部最优, 并在运行时出现迭代暂停的现象。人工萤火虫算法(GSO： Glowworm Swarm Optimization)[8]是近年来比较新颖的一种仿生算法, 它模拟了在一定范围内萤火虫发光越强吸引同伴越多的现象。该算法具有良好的全局搜索能力, 同时也存在着耗时多、 精度低等缺点。针对粒子群算法和人工萤火虫算法存在的不足, 研究者们已做出了部分改进, 文献[9]通过融合模式搜索, 加快算法收敛效率, 并求得精度较高的解; 文献[10]针对粒子群算法过早收敛且易陷于局部最优等缺陷, 将混沌序列引入初期粒子群, 从而构建新型的混沌粒子群混合优化算法; 文献[11]引入动态调整自适应步长的策略改进人工萤火虫算法; 文献[12]将引入混沌序列后的粒子群和经过权重修正的自适应策略相融合, 从而加速算法收敛。但是, 针对人工萤火虫算法或粒子群算法的单一改进不能突显出算法真正的优势, 使其具有一些局限性。因此, 笔者利用优势互补思想, 将粒子群算法与改进后的人工萤火虫算法结合, 搜索全局最优解, 在加快算法收敛速度的同时提高解的精度。

笔者针对ICP算法对初始点云位置要求高且易陷于局部最优的不足, 提出一种初始配准加精细配准的点云配准方法。首先, 改进人工萤火虫算法, 通过引入Logistic映射初始化种群, 并提出一种基于动态分组策略的自适应步长方法, 然后针对粒子群算法易于陷入局部最优的缺点, 利用优势互补的思想将改进后的人工萤火虫算法与粒子群算法结合, 把最小二乘迭代后搜索的最优结果作为粒子群算法最初的种群数据, 并利用该算法的优势搜索全局最优解。其次, 考虑到ICP算法配准需要较好的迭代初始位置才能收敛, 提出将初始配准和精细配准相结合, 在初始配准阶段使用改进后的人工自适应萤火虫-粒子群算法(AAGPSO： Adaptive Artificial Glowworm-Particle Swarm Optimization), 在之后的精细配准阶段使用ICP算法, 以提高配准精度与算法效率。对原始ICP配准方法和改进配准方法进行比较和误差分析表明, 改进后配准方法更加有效。

1 改进的自适应人工萤火虫粒子群算法

1.1 基本思想

人工萤火虫算法模仿萤火虫在一定的区域里发光越强, 吸引同伴越多的现象, 是一种最近几年发展起来的智能仿生算法[13-14]。该算法能较好地进行局部搜索, 但搜索时间长且准确度低。因此, 为给精细配准提供良好的初值, 提高配准效率和精度, 将人工萤火虫算法与粒子群算法相结合, 根据优势互补思想, 提出一种新型的混合算法： 自适应人工萤火虫-粒子群算法。

在搜索初期, 笔者首先将Logistic映射引入人工萤火虫算法, 利用混沌运动的遍历性混沌初始化算法, 将混沌序列引入人工萤火虫算法能均匀分布初始的萤火虫种群, 使算法的搜索效果更加显著, 从而解决人工萤火虫算法收敛速度慢、 解的精度低的问题。其次将位移权重引入算法, 并对位移权重进行调整, 然后将种群按照适应度值的分布进行分组从而提高算法的运行效率。最后串联以上算法生成一种新型混合算法为自适应人工萤火虫-粒子群算法。

自适应人工萤火虫-粒子群算法在算法前半阶段采用已优化的人工萤火虫算法, 将搜索到的解作为下半阶段粒子群算法的初始数据, 再通过粒子群算法搜索全局最优解。优化后的人工萤火虫算法能搜索到局部最优解, 粒子群算法提高了寻优的效率与精度, 使整体寻优过程得到优化。

1.2 种群初始化

对种群参数进行合理的初始化可增强算法的全局搜索能力, 从而提高所求解的精度。在人工萤火虫算法运行初期, 由于目标范围不确定且目标区域广阔而导致盲目搜索, 无法确定种群位置的最优解, 所以从种群初始位置开始寻找最优解已成为算法的基本操作。但若选择的初始种群零散分布或集中于某一区域内, 则算法在运行开始后会立即收敛到部分种群集中区域, 这种情况易使算法陷入局部最优解。因此, 笔者引入混沌序列初始化种群, 避免发生算法陷入局部最优区域的问题。

混沌运动[15]是一种确定系统中出现的具有遍历性的无规则运动, 能在一定的区域里按其自身不重复地遍历所有的状态。相比于无序随机搜索, 利用混沌变量进行搜索更能增强被搜索种群的多样性。因此, 笔者引入混沌序列, 在一定大小的搜索空间中使初始种群均匀分布, 以使算法所得解更加精准, 丰富搜索种群类别, 提高算法搜索能力。选择取值范围为(0,1)的混沌变量an, 范围为[0,4]的控制参数μ, 通过Logistic映射混沌初始化人工萤火虫算法, 其迭代式为

an+1=μan(1-an)

(1)

当μ∈[3.57,4.00]时, 可使序列an产生混沌状态[16]。将萤火虫的位置信息xi映射为混沌变量an

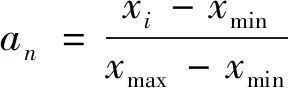
(2)

则xi=an(xmax-xmin)+xmin

(3)

1.3 自适应步长的调整

在人工萤火虫算法运算过程中, 萤火虫移动的步长会影响算法的收敛效果[17]。萤火虫个体较小的移动步长虽会使所求得的解更加精确, 但会在一定程度上降低算法的运行速率; 当步长值较大时, 种群个体移动较快, 可得到较好的收敛效果, 加快了算法运行速率, 但较大步长易使个体错过最优位置, 使解的精度较低。因此, 笔者选择基于动态分组策略对步长进行自适应调整, 在保证算法收敛速度的同时将解的精度提高。设人工萤火虫的位移惯性权重为ωs, 依据粒子群算法中惯性权重调节粒子速度的原则, 将人工萤火虫算法位置更新为

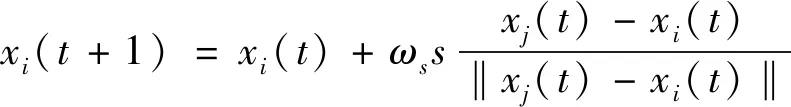
(4)

其中s为移动步长,xi(t)为第i只萤火虫在时刻t位置。

调整自适应步长时, 种群质量不同, 赋予的权重也不同。对比个体平均适应度值, 将种群分为3类： 优秀种群、 一般种群和较差种群。对于优秀种群, 往往选取较小的移动步长并赋予较小权重, 从而加速算法全局收敛; 对于一般种群, 种群个体的位移权重始终被设置为固定值, 从而平衡全局搜索和局部搜索能力; 对于较差种群, 将其剔除, 并以一般种群的最优个体为圆心, 萤火虫感知范围为半径, 随机生成与所剔除的种群数相匹配的新种群, 从而达到丰富种群的种类、 增强算法的全局性的效果。

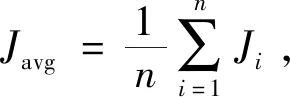
步长的自适应调整策略的具体步骤如下。

1) 对第1组优秀种群动态调整位移权重

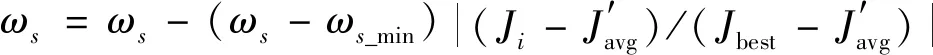
(5)

其中ωs_min是已经定义的位移权重的最小值。

2) 使第2组一般种群的位移权重保持为固定值。

3) 剔除第3组较差种群, 以一般种群中比较优异的个体为圆心, 萤火虫感知范围rs为半径, 随机生成新种群代替被剔除的较差种群。

1.4 自适应人工萤火虫粒子群算法流程

通过上述思想, 将人工萤火虫算法与粒子群算法相结合, 得改进后的自适应人工萤火虫-粒子群算法的流程图如图1所示。

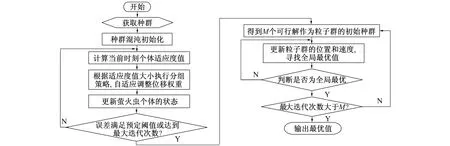
图1 AAGPSO算法流程图Fig.1 AAGPSO algorithm flow chart

2 基于ICP优化算法的点云配准

2.1 基于权重策略剔除噪声点与误匹配点对

点云数据配准[18]即在两个点云集中找到一一对应的数据点, 并将其转换到同一个坐标系中, 获得一个完整的三维点云数据的计算过程。在进行点云数据配准时, 根据位置与方向不同将其分为两阶段, 即初始配准和精细配准[19]。初始配准即全局配准, 在初始配准过程中, 两片重叠率低的点云数据被拉近, 减小点云之间的旋转和平移造成的误差, 从而为后续的精细配准打下基础。

在点云配准过程中, ICP算法默认最好配准效果是待匹配点云的对应点是一一对应的, 没有其他干扰存在, 但在算法实际配准的过程中, 点云之间若存在未完全包含关系, 则会出现许多噪声点和误匹配点对, 造成较大配准偏差[20]。

基于ICP算法配准偏差较大的特点, 笔者提出一种基于权重策略的噪声点与误匹配点对解决办法。该方法首先通过限制距离权重, 计算待匹配点对的欧氏距离, 去除低于阈值的噪声点, 其次通过限制特征权重, 计算匹配点法向量之间的夹角, 去除低于阈值的错误匹配点对。具体描述如下。

1) 限制距离权重。对应点对之间的距离信息在确定对应点对的同时将被获取, 当获取的两个对应点对之间的距离过大时则认为该对应点对是噪声点。所以笔者对距离权重进行限制, 即距离越大其权重越小的思想, 将噪声点去除, 设定阈值ε1, 则引入的距离权重

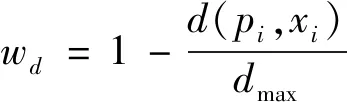
(6)

其中d(pi,xi)为对应点pi和xi的欧式距离,dmax为对应点pi和xi之间的最大距离。如果计算得出的距离权重wd小于事先给定的阈值ε1时, 则该对应点对被判定是噪声点且在点云中删除该点对。

2) 限制特征权重。虽然限制距离权重可确定点云中的噪声点并对噪声点进行适当的去噪处理, 但在对应点对中依旧有一部分无法去除的噪声点。虽然点云中的对应点集所处的坐标系不同, 但待匹配的点云之间的空间拓扑关系大概一致, 都可经过平移和旋转而进行变换。基于以上原理, 笔者使用特征权重, 即特征越一致其权重就越大的思想, 将误匹配的点对去除。其中方向一致性特征权重

wn=n(pi)·n(xj)

(7)

其中n(pi)和n(xj)分别表示对应点对pi和qj的法向量, 其法向量估计方法定义如下。

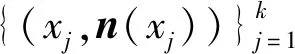
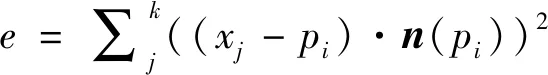
(8)

最小。

应用最小二乘法, 可得到以下3×3矩阵

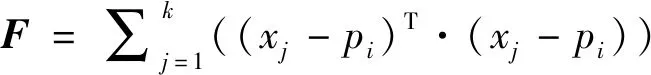
(9)

其中F的最小特征值对应的特征向量即可作为法向量n(pi)的近似值。

2.2 改进算法描述

在基于深度图像的三维重建领域中, 三维点云配准一直是不可缺少的一步。在诸多配准算法中, ICP算法最为著名。但ICP算法仍具有许多局限性有待改进：当点云所包含点的数量大规模增长时, 其搜索时间复杂度随之增长, 不利于实际应用; 当待匹配的点云初始位置距离较远时, ICP算法的收敛速度变慢, 算法容易陷入局部最优, 从而降低配准效率及精度; 当直接对不满足包含关系的点云进行对应点对的搜索时, 可能产生错误的匹配点对, 使最终的匹配结果受到影响。

针对以上问题, 笔者对ICP算法进行改进, 提出一种优化的点云配准方法, 在ICP算法中引入AAGPSO混合算法。运用AAGPSO算法确定初始点云位置, 计算更新后的适应度值, 当最佳适应度值增量小于给定的阈值0.01时, 初始配准结束, 然后继续采用ICP实现精细配准。此方法避免了配准的盲目性, 能对配准过程进行优化, 在保证算法鲁棒性的同时, 提高了点云配准的效率和精度。改进后的AAGPSO-ICP混合算法具体实现步骤如下。

Step2 对源点集P构建kd-tree, 并搜索源点集P最近点已确定的对应点对。

搜索具体过程如下。

1) 输入kd-tree判断点云数据是否为空, 若为空则返回空值。

2) 进行二叉搜索[21]。首先判断当前进行搜索的节点, 若不是叶子节点则将该节点与分割轴在当前维度下进行比较, 将小于分割轴的点转向左子树比较, 否则转向右子树比较。然后在子树中重复上述方法, 当搜索节点为叶子结点时, 停止搜索比较, 计算该结点与叶子结点之间的距离, 记录当前最近邻点的信息, 并保存最近距离。

3) 对搜索过的路径进行回溯查找, 判断没有被访问的分支中是否存在更接近当前节点的数据点。如果有, 则进入之前未被访问的分支查找更近的点, 并将最近邻点更新, 所有分支节点全部检查完毕后, 输出最新的最近邻点及最近距离。

Step3 根据2.1节, 使用距离权重与方向权重剔除噪声点与误匹配点对。

Step4 初始化参数m、rx、ry、rz、tx、ty、tz, 其中rx、ry、rz为旋转变量,tx、ty、tz为平移变量,m为缩放参数。

Step5 计算旋转变量和平移变量, 令m=1。

Step6 计算旋转平移变换点集

Xn=RX+T

(10)

计算适应度

f=‖RX+T-Xn‖+‖RN-Nn‖

(11)

其中X为目标点云数据集,R为旋转变量点集,T为平移变量点集,N为点集X的法向量,Nn为点集Xn的法向量。对上述适应度函数建立两个约束条件： 1) 对应点对间的距离最小; 2) 法向量间的夹角为零。

Step7 应用新生成的混合算法AAGPSO对粒子的速度和位置进行更新, 计算更新后粒子的适应度值f, 若其小于给定的阈值, 则迭代终止, 输出点云集Xn, 将其作为精细配准的初始点云集数据; 否则返回Step3重新配准。

Step8 计算源点集Pn在目标点集Xn中的最近点集Yn=C(Pn,X), 将其作为对应点集。

Step9 求解变换矩阵并计算误差： (qn,dn)=υ(P0,Yn), 其中d表示对应点匹配的均方误差。源点集在刚体变换向量q的作用下更新至新的位置P0。

Step10 根据求得的变换矩阵更新点云位置, 并判断误差向量是否小于给定阈值。若是, 令原点集与目标点集匹配, 得最终配准结果; 否则, 转至Step8。

3 点云配准实验与误差分析

为验证改进后的基于混合算法的点云配准方法的有效性, 首先设置改进算法各项参数。设置萤火虫初始荧光素值为5, 荧光素挥发系数为0.4, 移动步长为0.3, 荧光素更新率为0.6, 萤火虫感知半径为6.12, 粒子群优化算法中设置学习因子为2, 惯性权重为[0.4,0.9]。使用斯坦福大学提供的.ply格式的标准模型, 分别用原始的ICP点云配准算法和改进后的点云配准方法对点云数据进行配准, 分析实验结果[23-24]。为使实验数据不受外界因素干扰, 实验环境统一使用联想电脑, CPU处理器为i7-6700, 主频为3.1 GHz, 内存为8 GByte。

3.1 点云模型配准实验结果分析

通过运用原始的ICP算法和笔者提出的改进后方法分别对fish和bunny点云模型进行点云配准实验, 其中fish点云模型共有3 164个点, bunny点云模型共有83 341个点。配准实验效果图如图2和图3所示。

a fish点云的初始位置 b 原始ICP算法配准效果 c 笔者改进方法配准效果图2 ICP算法与笔者算法对fish点云模型配准效果对比Fig.2 Comparison between the ICP algorithm and new algorithm of fish point cloud model

a bunny点云的初始位置 b 原始ICP算法配准效果 c 笔者改进方法配准效果图3 Bunny点云模型配准效果对比Fig.3 Bunny point cloud model registration effect comparison

对比图2b、 图2c可知, 改进算法比原ICP算法配准效果更佳。原始ICP算法配准后仍存在一些误差, 而改进方法在原有ICP算法基础上提高了配准精度。通过对比图3b、 图3c可知, 原始ICP算法在配准精度上并不高, 而笔者方法可达到完全重合的效果, 配准精度明显提升。

通过上述两个实验可知, ICP算法和笔者提出的配准方法均能完成点云配准实验, 但当点云中的点增多时, ICP算法点云配准效果明显比笔者的方法误差更大, 配准的完成度更低。笔者提出的配准方法使两片点云重叠的效果优于原始ICP算法。

3.2 误差分析

误差计算使用文献[22]的方法, 其配准误差参数

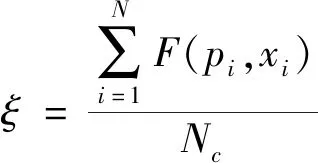
(12)

其中Nc为点云的数据量, 未达配准精度判断函数

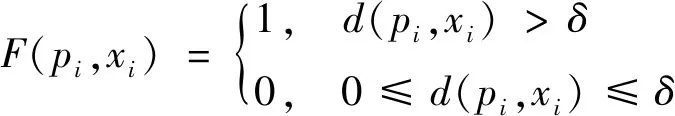
(13)

其中δ为给定精度,d(pi,xi)为两片点云中的对应点对(pi,xi)经过配准后的距离。

两种配准方法误差对比如表1所示。从表1可见, 相比于原有的ICP算法, 笔者提出的方法配准精度大幅提高, 并将配准误差减小至0.018%。

3.3 配准速度分析

笔者采用Fish和Bunny两组点云模型进行点云配准[25], 并分别记录两类点云数据的匹配时间, 结果如表2所示。

表1 配准误差对比

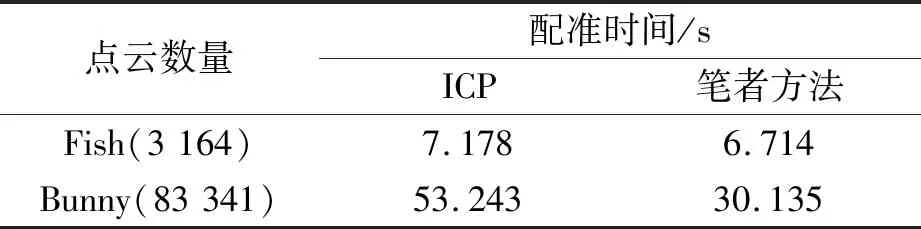
表2 配准的运行速度对比

由表2可知, 当点云数量增多时, ICP和笔者算法耗时都比较多, 但点云数量相同时, 笔者提出算法的运行时间要优于原ICP算法, 并且配准效率随着点云数量的增加而提高。

综上, 通过对比传统的ICP算法和笔者算法对相同点云模型配准后的误差分析和配准速度可见, 笔者提出的AAGPSO算法在传统ICP算法的基础上提高了配准精度, 并且加快了算法的收敛速度。

4 结 语

笔者根据优势互补的思想, 针对粒子群算法易陷入局部最优的问题, 对人工萤火虫算法改进并与融合粒子群算法, 提出了一种自适应人工萤火虫粒子群混合算法, 在保证鲁棒性的前提下, 加快算法收敛速度, 提高解的精度。然后, 将AAGPSO算法引入ICP算法而产生新的点云配准方法, 利用AAGPSO算法确定点云的初始范围, 解决了ICP算法在寻优过程中由于点云初始位置的差异过大而陷入局部最优的问题, 缩小对点的搜索范围的同时加快了配准效率。最后, 通过实验对原始ICP配准方法和笔者配准方法进行对比与误差分析, 结果验证了改进配准方法的有效性。