基于特征提取的网贷平台生存关键因素研究

于卓熙, 温 馨, 李梦丽

(吉林财经大学 管理科学与信息工程学院, 长春 130117)

0 引 言

P2P(Peer-to-Peer)网络借贷是借贷双方不经过金融中介机构, 直接通过网络平台进行借贷的一种互联网金融模式。P2P网贷起源于发达国家, 良好的经济环境促进P2P网贷运营模式的形成。但欧美发达国家人口基数较低, 客户较少, 因此P2P网贷的发展受到限制。反之, 中国现在虽为发展中国家, 但巨大的人口市场为P2P网贷提供了欧美国家欠缺的成长机会。P2P的壮大为“贷款难”群体带来福音。中小型企业以及小工作坊虽然个体规模较小, 但却占据了中国市场经济的半壁江山, 而传统银行信贷在很大程度上受货币政策影响, 货币政策比较宽松, 银行信贷也会比较宽松; 若货币政策趋向紧缩, 银行信贷也随之趋向紧缩, 中小企业的融资难问题将更为严重。P2P网贷的审批, 对货币政策和信用等级的敏感性比较弱, 多数的P2P网贷平台一般具备流程简单、 快速到账的优点; 通过P2P网贷, 社会中的闲置资本流入到制造业或消费市场中, 有利于社会资源的合理配置。因此, 为促进P2P行业成熟, 推动社会经济发展, 进行P2P网络借贷研究是十分必要的。

国外对于P2P网贷的研究较早, 成果比较丰富。在P2P网贷借贷模式方面, Wang等[1]认为一般意义上的网络借贷是一种新型借贷模式; Livingston[2]认为这种网络借贷模式具有3个基本特征, 分别是贷款额度较小、 过程比较便捷和几乎没有担保; 部分国外学者对于P2P网贷研究围绕信用和风险进行, Bachmann等[3]依据人口学特征, 结合类似朋友、 群组的社会特征并综合财务情况等对P2P平台借款人进行分类, 研究借款人特征和借款成功与否之间的关系; Ceyhan等[4]选取Prosper平台一段时间内的实际交易数据, 对借款利率和平台投标数量随时间的变化情况进行研究, 发现对于未满足投标数量的标, 投标者越多, 则后续投资者会呈现一种明显的“跟风”, 即出现“羊群效应”; Lin等[5]的研究表明借款者的信用与贷款利率、 坏账率呈反向关系; Pokornám等[6]的实证结论表明, 较高的盈利能力、 流动性和资产规模意味着违约风险较低, 而高负债和高杠杆意味着违约风险较高。收益率作为影响借贷人和投资者选择平台的重要因素受到很多学者的关注, Greiner等[7]以借款人的信用状况, Gonzalez等[8]选择借款人的图片信息, 探索P2P网贷收益率的影响因素。

虽然国内P2P网贷起步较晚, 但关于P2P网贷的风险及监管方面的理论研究较多。吴晓光等[9]从用户识别、 资金管理以及信用评级等方面为P2P网贷的完善提出了建议; 黄震等[10]在研究中指出, 我国应参照英国, 构建P2P网贷行业自律和与法律结合的监管体系; 沈良辉等[11]通过对国外P2P网贷信用风险防控经验研究, 结合我国实际, 从政策、 风险控制机制以及征信系统几方面提出意见; 潘锡泉[12]在研究中较为全面地指出, 存在四大风险阻碍我国P2P借贷行业发展, 分别是信用风险、 没有保障的信息技术风险、 不健全的政策法规风险以及包含法律道德的操作风险, 并针对四大风险提出建议和对策以推进P2P网贷健康发展; 杨立等[13]以信息经济学和博弈论为基础, 建立信息不对称的理论模型, 从事前、 事中、 事后3个环节分析P2P借贷信用风险成因, 讨论社交网络缓解信用风险的机制及其作用条件。实证分析方面大多集中于网贷平台信用研究, 曾江洪等[14]利用拍拍贷数据, 研究P2P网贷市场的“羊群效应”; 肖曼君等[15]利用多个P2P网贷平台的数据, 通过排序选择模型进行平台信用影响因素研究; 唐艺军等[16]以“陆金所”平台用户为例, 对网贷信用风险进行实证研究; 王立勇等[17]采用2层次CRITIC-灰色关联模型构建风险评价体系, 运用Var方法测算风险大小, 发现2014年前3个季度平台整体风险较高, 第4季度在市场风险下降的作用下信用风险呈下降趋势。邵蔚[18]对P2P平台运营模式的国内外研究进行梳理和阐述, 利用决策树模型对平台进行是否“跑路”做出预测, 对信用风险做量化评估, 发现决策树预测方法准确度可达77.08%, 为相关投资者提供决策依据; 蒋翠清等[19]结合P2P平台信息特点, 提出一种融入软信息的网络借款违约预测方法; 梁寒冰等[20]采用熵值法-CRITIC双重客观赋权法确定指标权重, 通过GRA(Grey Relation Analysis)的改进方法综合评价P2P网贷平台信用风险。

P2P网贷于2007年登陆中国, 近几年才发展壮大起来, 按照企业生命周期, 应处于上升阶段。但据网贷之家2015年的数据显示, 当年问题平台的数量持续增加, 甚至出现当月新增的问题平台数量超过新增的平台数量。P2P网贷是新兴行业, 还没有进入衰退期, 因此P2P网贷平台大规模的“死亡”现象是值得关注的问题。而国内外对P2P行业的研究大多集中于借贷模式、 风险与监管的理论研究以及信用风险实证研究等方面, 关于P2P网贷平台“生存”或“死亡”的影响因素深度挖掘的研究成果较少。

笔者选取网贷之家公布的2014年度 P2P网贷平台百强名单中的网贷平台作为研究样本, 在数据一致性、 完整性及可获性条件下, 尽可能多地选择平台的属性变量。针对实际数据集, 利用随机森林分类和装袋法的思想, 对P2P网贷平台的多个变量进行初步分类, 按照重要性原则, 提取导致P2P网贷平台成为问题平台的重要变量。运用生存分析对影响P2P平台“死亡”的重要因素做进一步的量化研究, 通过拟合加速死亡模型和Cox比例风险模型, 挖掘影响平台“生存”或“死亡”的关键因素, 并量化该因素对P2P“生存”或“死亡”的影响程度。

1 特征变量提取方法

决策树是最基本的变量分类方法, 决策树的核心思想是在一个数据集中找到一个最优特征, 然后从这个特征的选值中找一个最优候选值, 根据这个最优候选值将数据集分为两个子数据集, 然后递归上述操作, 直到满足指定条件为止。基于决策树的分类方法简单且易于理解, 常见的有装袋法、 随机森林和提升法。笔者使用装袋法和随机森林法对特征变量进行分类和提取。

1.1 装袋法

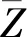
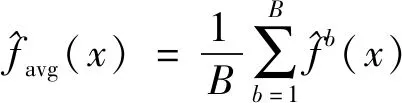
(1)

装袋法算法具体步骤如下：

1) 假设k为样本集的数目;

2) 生成k个大小为n的数据集, 每个自助样本集都和原数据集一样大;

3) 在k个样本集上训练分类器;

4) 投票决定分类结果。

1.2 随机森林

由于传统模型具有精度不高, 易出现过拟合问题, 需通过集成方法聚集多个模型提高精度。赵伟卫等[21]利用互信息快速排除一部分无关变量, 降低样本空间的维数; 利用随机森林精选剩余变量, 实验结果表明, 该算法具有更高的分类精度和泛化能力。随机森林是集成决策树的一种方法, 最早由Breiman[22]提出。首先, 利用bootstrap从原始样本集中进行重抽样抽取多个样本组成新的训练集, 对每个训练集进行决策树建模, 得到多个决策树, 最后通过组合与投票得到最终分类结果。

随机森林随机选择几个而不是全部的变量作为拆分变量, 每棵树都充分生长, 根据一定规则得到合适的决策树数目, 通过变量重要性对特征变量进行提取。随机森林算法步骤如下：

1) 利用bootstrap从原始样本集中抽取容量相同的k个样本;

2) 对抽取出的k个样本, 建立对应k个决策树, 得到k个分类结果;

3) 根据k个分类结果进行投票决定最终结果;

4) 计算不同决策树数量的袋外数据(OOB： Out of Band Data)误分率, 以OOB误分率较小为优, 确定决策树数目;

5) 依据变量重要性, 提取比较重要的变量。

随机森林随机选择少数自变量参与变量拆分, 使弱势变量可以参与建模, 在处理观测值少而自变量较多数据中显示出一定优势。

2 生存分析模型

生存分析是一门研究生存现象和响应时间数据及其统计规律的学科。该方法被广泛应用于医学领域。在医学研究中, 常常用追踪的方式研究事物发展的规律。如, 了解某药物的疗效、 手术的存活时间及某医疗仪器设备使用寿命等。对生存资料的分析称为生存分析。生存资料是描述寿命或一个发生时间的数据, 更详细地说, 一个人的生存时间的长短与许多因素有联系, 研究因素与生存时间有无联系及联系程度的大小称为生存分析。实际上, 生存的意义很广泛, 它可指人或动物的存活(相对于死亡), 可指患者的病情正处于缓解状态(相对于再次复发或恶化), 还可指某个系统或产品正常工作(相对于失效或故障), 甚至可指客户的流失与否、 企业的持续发展(相对于破产倒闭)等。因此, 该方法已经被延伸到很多领域, Lane等[23]运用生存分析中的Cox比例风险模型对银行经营困境进行研究; 贺筱君等[24]采用生存模型较好地预测了台湾隔日加权股价指数期货涨跌的持续时间; 鲍新中等[25]将生存分析应用于企业财务困境的研究; 张红等[26]使用生存分析方法建立Weibull模型和Cox模型进行实证分析, 研究二手房议价时的影响因素。笔者将生存分析应用到对P2P网贷平台的相关研究中, 探究影响P2P网贷平台“生存”或“死亡”的关键因素, 并根据分析结果提出有意义的建议。

2.1 加速死亡模型

生存时间是一个随机变量, 取值永远不会为负值。假设每个研究样本的生存时间可被精确预测, 表示为ti, 且xi=(xi1,…,xip)′表示第i个病人与其生存时间ti相关的解释变量。借鉴传统回归模型的思想, 将ti进行对数处理, 构造模型

logti=xiβ+ei

(2)

其中ei为残差项, 也可被认为没有变量影响的生存时间, 可记为logti0。因此该模型可以转化为

logti=xiβ+logti0

(3)

则

ti=ti0exp(xiβ)

(4)

通过式(4)可知, 没有变量影响, 则生存时间为ti0, 加上相关变量的影响, 生存时间被“加速”成为ti0exp(xiβ)。

2.2 Cox比例风险模型

由英国伦敦大学的著名统计学家Cox提出的Cox模型不仅可应用于对个体生存时间的多个影响因素分析和比较研究中, 还可用于对个体做生存(或死亡的)风险预测。笔者使用Cox比例风险模型, 通过最大化似然函数的方法进行模型拟合, 其形式为

h(t)=h0(t)exp{βx}

(5)

其中h0(t)表示基准风险函数, 即没有其余变量影响的死亡事件发生的函数。式(5)表示, 在变量x的影响下, 死亡事件基准函数被等比例扩大了exp{βx}倍。

3 数据来源与数据处理

P2P借贷平台众多, 背景各异, 一些快速崛起的平台可能在短时间陷入经营困境。为此, 笔者选用实力较强的P2P借贷平台作为研究对象, 以网贷之家2014年发布的100强名单中的P2P平台为研究数据集。由于部分平台数据严重缺失, 最终选取100强平台中的90家平台(其中74家正常平台, 16家死亡平台)作为研究对象, 探究影响P2P生存的关键因素。造成P2P借贷平台经营困境的原因错综复杂, 笔者在依托前人研究成果的基础上, 结合文献查阅, 确定13个变量, 分别为平台背景(平台类别)、 平台注册资金(以实际认缴资金为准)、 用户资金银行存管情况、 是否支持自动投标、 是否支持债权转让、 是否有保障模式、 风险准备金银行存管情况、 借贷平台网址等级、 年平均收益率、 平台所在地城市等级、 上线时间、 生存状态、 生存时间。进行生存分析的时间从2015年1月开始到2017年6月结束, 90家平台在这个期间的生存状态是74家平台正常运行(正常平台), 16家平台倒闭或“跑路”(问题平台)。

为保证后续实验的顺利进行, 笔者对上述P2P网贷平台变量进行命名, 并对生存状态、 平台类别、 注册资金(以实际认缴为主)、 用户资金银行存款、 自动投标、 债权转让、 保障模式、 风险准备金存管、 网址等级、 平均收益、 所在地区和上线月数等指标进行说明, 其中生存状态为后文进行生存分析做准备, 在分类中不参与实验。具体变量说明如表1所示。

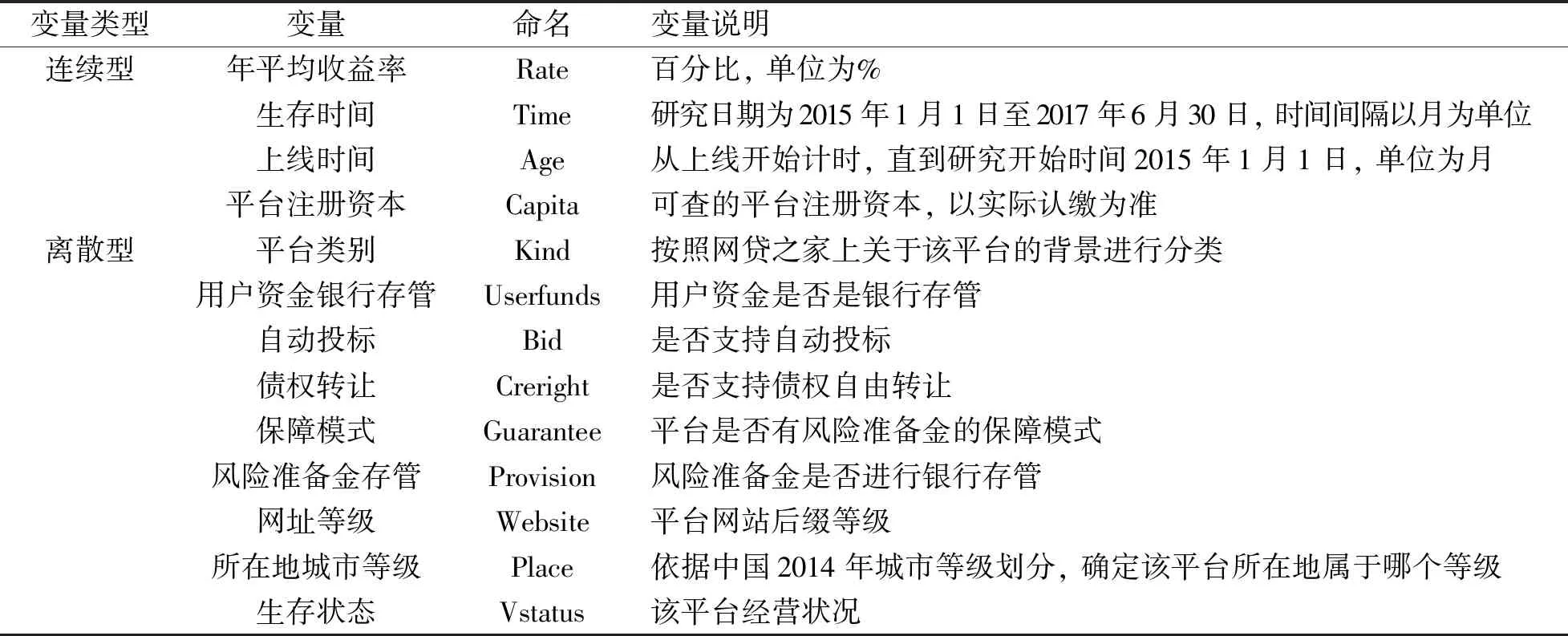
表1 变量说明

上述变量中存在字符型变量, 为保证实验顺利进行, 笔者依据问题平台(停业、 坏账和跑路)和正常平台分类方式, 对数据集进行处理, 结果如表2所示。

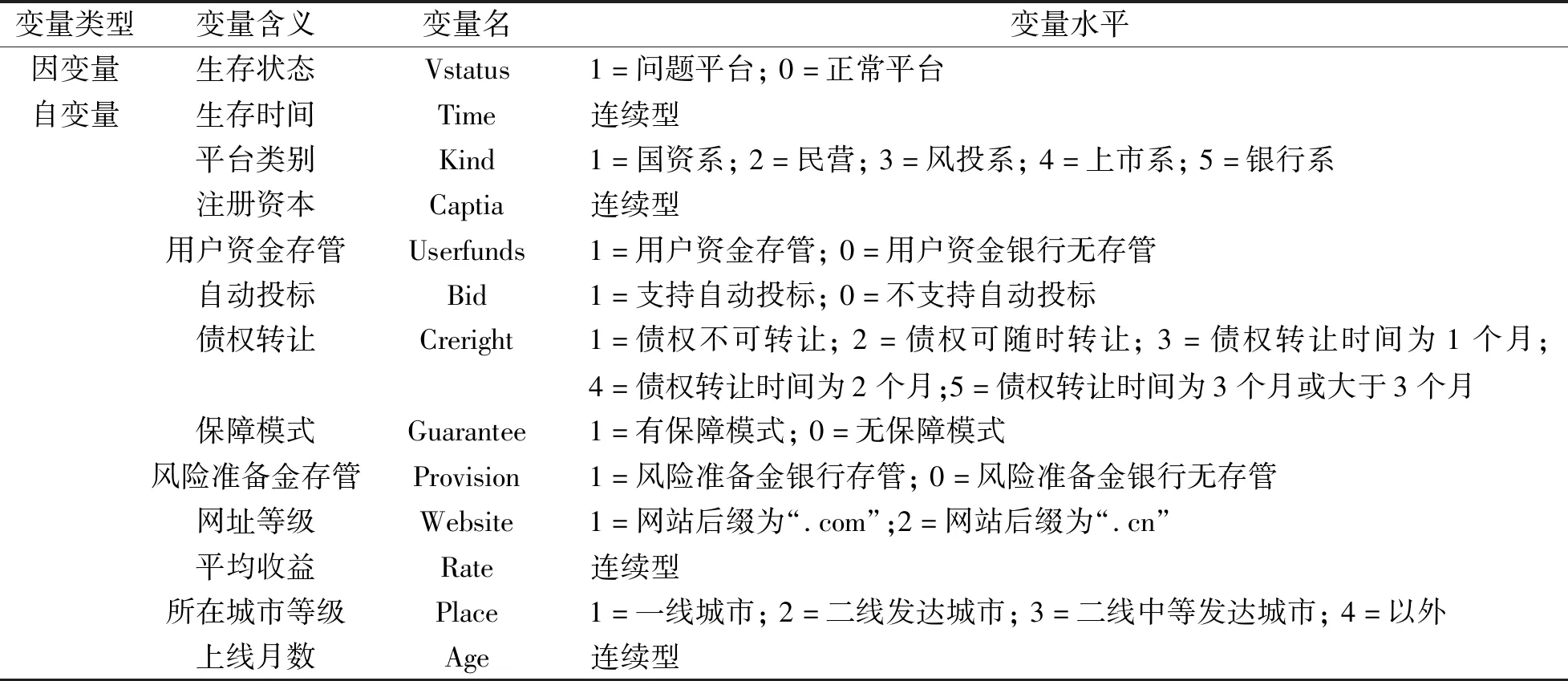
表2 变量处理

笔者实验的数据主要来自于网贷之家、 网贷天眼、 我贷网和零壹财经等网站。经过处理后的部分数据如表3所示。

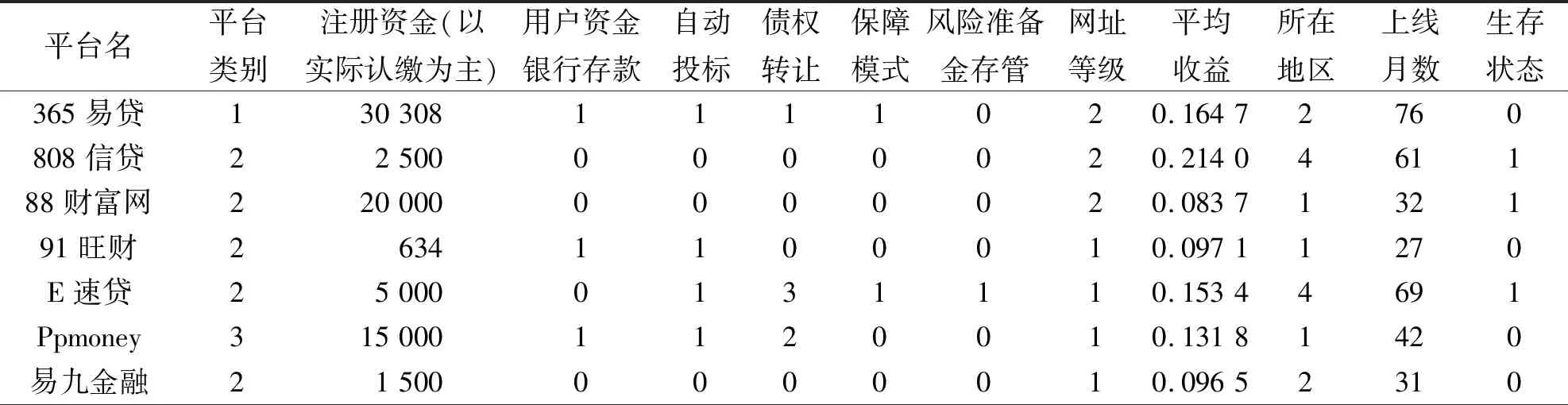
表3 P2P分类研究部分数据

(续表3)

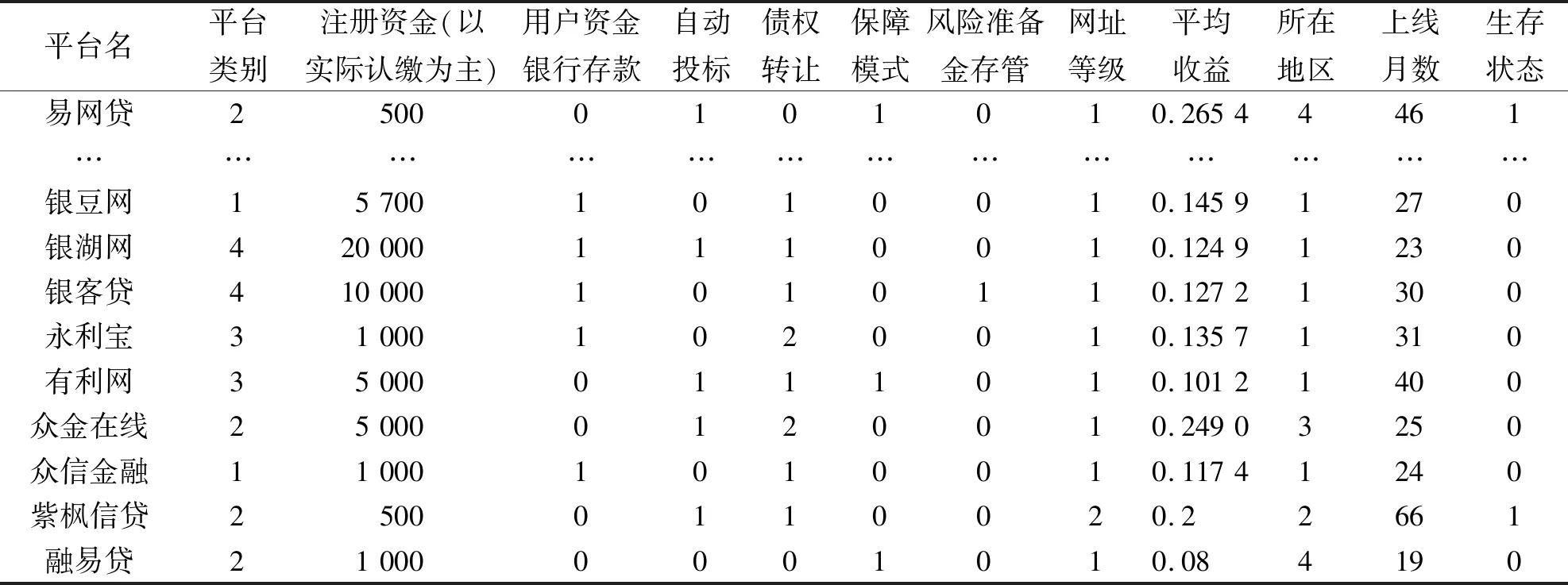
平台名平台类别注册资金(以实际认缴为主)用户资金银行存款自动投标债权转让保障模式风险准备金存管网址等级平均收益所在地区上线月数生存状态易网贷25000101010.26544461…………………………………银豆网157001010010.14591270银湖网4200001110010.12491230银客贷4100001010110.12721300永利宝310001020010.13571310有利网350000111010.10121400众金在线250000120010.24903250众信金融110001010010.11741240紫枫信贷25000110020.22661融易贷210000001010.084190

4 平台分类与重要变量提取

4.1 装袋法分类

首先, 采用装袋法, 对P2P网贷平台进行分类研究, 装袋法会对所有样本集进行训练。在实验过程中, 采用自带的十折交叉验证运行装袋法, 对样本数据集进行分类, 装袋法的分类结果如表4所示。

表4 装袋法分类结果

如表4所示, 装袋法的误判率在可接受范围。分类中共有4种变量重要性度量方法, 笔者采用Gini指数法。Gini指数表示节点的纯度, Gini指数越大, 表示该拆分节点纯度越低。Gini值平均降低量表示所有树的变量分割节点平均减小的不纯度, Gini指数变化的均值作为变量的重要程度度量。变量重要性度量

结果如表5所示。

表5 装袋法变量重要性度量

根据表5可知, 按照生存状态使用装袋法对P2P平台数据集进行分类, 影响分类结果的重要变量依次是Age、 Rate、 Capita、 Userfunds和Kind。

4.2 随机森林分类

随机森林和装袋法类似, 也是从原始数据中抽取一定数量的自助法样本, 区别在于, 使用随机森林分类时, 所选择的竞争变量是随机的几个, 不是全部。为更全面地进行探索研究, 继续以随机森林方法进行P2P正常平台和问题平台的分类。

4.2.1 确定决策树数目

随机森林分类过程中, 决策树数目的选取在一定程度上影响着精度。随着决策树和变量的增加, 误差(MSE： Mean Squared Error)会降低。笔者应用R软件中程序包randomForest 中的randomForest函数生成决策树, 该程序默认决策树数目为500。经实验, 误差随决策树数目变化趋势如图1所示。

从图1可以看出, 随着树的数目的增加, 误差逐渐趋于稳定, 决策树数目取值200就可以满足实验要求。

4.2.2 寻求节点最优竞争变量个数

随机森林分类过程中, 对于每个节点, 大约只有1/3的变量被随机选出。为此, 笔者根据OOB误差, 计算最优竞争变量个数, 筛选出进行后续生存分析的变量, 结果如图2所示。横坐标为竞争变量个数, 纵坐标为OOB误差, 对于该数据集, 当节点的竞争变量数目从4个增加到6个时, 误差显著增加; 变量从4个减少到3个时, 误差也增加。因此, 最终确定最优变量数目为4。

4.2.3 实验结果

随机森林分类中, 为进行随机分类结果检验, 笔者在原有数据集的基础上, 选择不同大小的数据集作为验证集。值得注意的是, 问题平台类别都是民营系, 这与市场中民营系平台较多是分不开的。因此, 如果只是随机选择平台, 可能导致实验结果中平台背景作为影响正常平台和问题平台的特征较为突出。针对这个问题, 笔者选择两种数据集: 一种是有选择性地保留正常平台中的民营系平台的数据集; 另一种是验证全部数据的分类结果。应用R软件进行实验, 两种数据集的分类结果如表6所示。

表6 随机森林不同数据集分类结果

同理, 依据Gini系数进行变量重要性排名, 两种数据集变量重要性度量结果如表7所示。

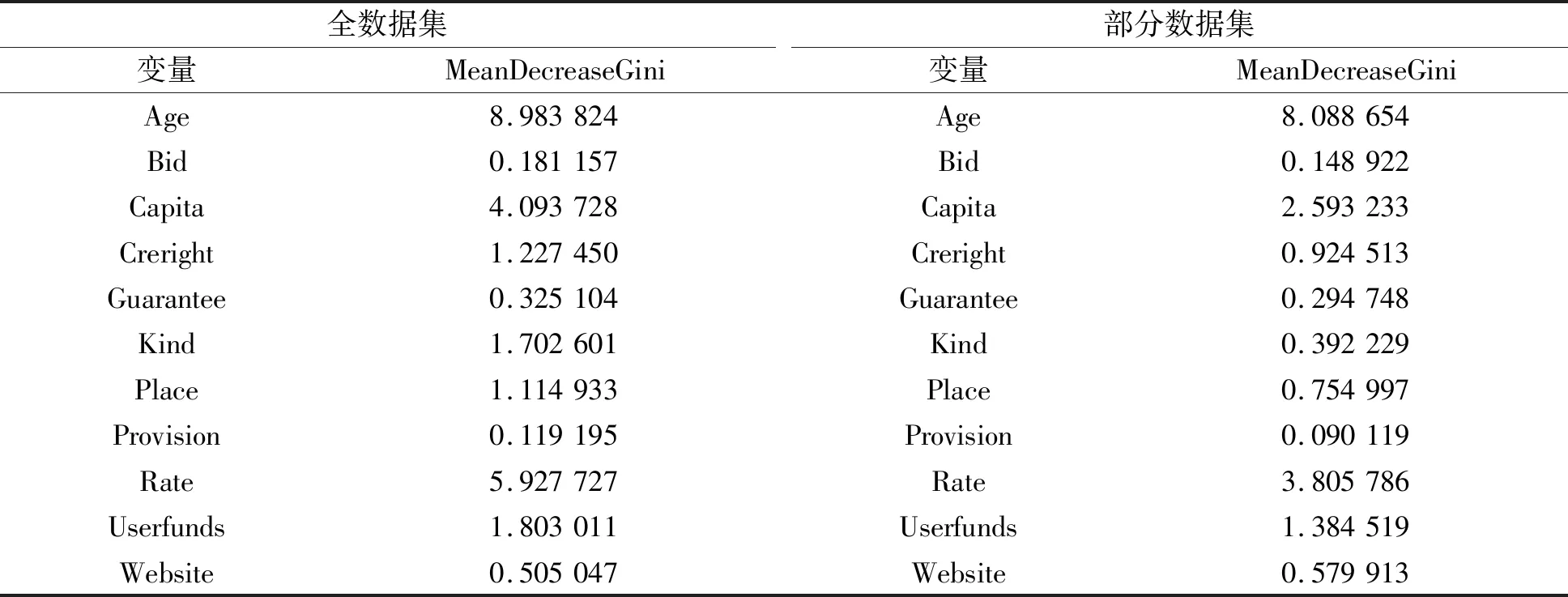
表7 随机森林不同数据集变量重要性程度度量

从表7可见, 全数据实验结果表明, 影响P2P正常平台和问题平台分类结果的变量按重要性程度依次为Age、 Rate、 Capita、 Userfunds、 Kind、 Creright 和Place, 其余变量重要性可忽略不计。选择部分数据集进行P2P正常平台和问题平台分类, 变量重要性程度排名依次为Age、 Rate、 Capita、 Userfunds、 Creright、 Place和 Website。

综合上述两种变量分类方法, 可确定影响P2P网贷平台成为问题平台最重要的变量为Age、 Rate、 Capita和 Userfunds。因此, 对网贷平台投资者和监管者而言, 在做出决策或制定相关政策时, 需从Age、 Rate、 Capita和 Userfunds4个方面进行着重考虑。

5 拟合生存分析模型

生存分析中最基本的函数是样本在事件发生时的生存率。估计生存率的方法主要包括寿命表法和Kaplan-Meier法。如果样本数量较大, 可使用寿命表法; 如果样本数量较小, 则选择Kaplan-Meier法比较适宜。Kaplan-Meier法又被称为极限估计、 PL(Product-Limit)法或最大似然估计。笔者样本为网贷之家2014年P2P网贷平台的百强平台, 样本数量较小, 适合用Kaplan-Meier法估计生存率。

5.1 拟合加速死亡模型

为量化上述Age、 Rate、 Capita和Userfunds 4个因素对P2P网贷生存或死亡的影响, 首先应用生存分析中常用的加速死亡模型进行拟合。假设残差项服从Weibull分布, 拟合结果如表8所示。

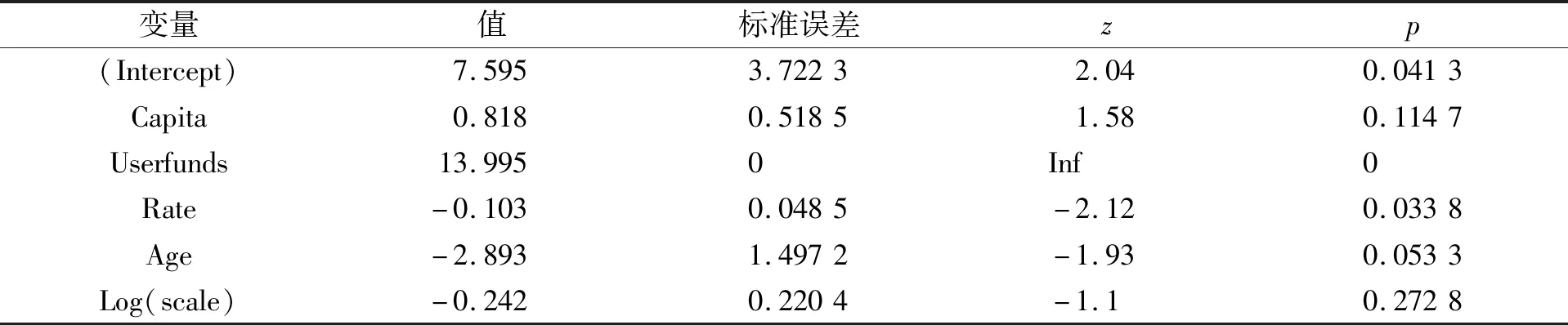
表8 加速死亡模型拟合结果(Weibull分布)

极差: 0.785; 韦布分布; 对数似然(模型): -75.8; 对数似然(只有常数项): -95.8; 对数似然(模型): -75.8; 对数似然(只有常数项): -95.8; 牛顿-拉斐逊迭代次数: 20。

根据实验结果, 模型拟合的p值为3.2×10-5, 模型整体显著, 理论上可对生存状态进行解释。从表8可见, 在显著性水平为10%的条件下, Capita、 Userfunds、 Rate和Age 4个变量都对P2P平台的生存有显著影响。加速死亡模型拟合结果表明, 变量Capita和Userfunds系数为正, 说明平台Capita和Userfunds这两个变量值越大, 生存时间越长; 反之, 变量Rate和Age系数为负, 说明Rate和Age这两个变量值越大, 平台生存时间越短。加速死亡模型将对数变换后的生存时间和普通线性模型联系起来, 直观且易被接受, 但缺点是模型的假设性太强, 需要对残差分布作严格假设。因此, 为考察模型的稳定性, 假设残差项服从指数分布, 再次对加速死亡模型进行拟合, 拟合结果如表9所示。

表9 加速死亡模型拟合结果(指数分布)

指数分布; 对数似然(模型): -76.3; 对数似然(只有常数项): -95.8; 自由度为4的卡方值: 39.04;P值： 6.8×10-8; 牛顿-拉斐逊迭代次数: 19。

根据表9可知, P2P网贷平台生存分析的数据对于不同的误差分布假设并不敏感, 因此利用加速死亡模型得到的结论比较可靠。

5.2 拟合Cox比例风险模型

为获得更全面、 可靠的结论。笔者建立Cox回归模型对各个因素导致P2P网贷生存或死亡的影响程度进行量化研究。但在模型构建前, 需对4个变量分别进行Log Rank (Mantel-Cox)检验, 进行再次筛选, 判断每个变量是否有必要纳入到Cox比例风险回归模型中, 笔者使用SPSS(Statistical Product and Service Solutions)软件进行检验, 检验结果如表10所示。

表10 变量Log Rank (Mantel-Cox)检验结果

从表10可见, Capita、 Userfunds、 Rate和Age 4个指标的p值均小于0.01。因此, 在显著性水平为1%的条件下, 4个变量均可以被纳入到Cox比例风险回归模型中。在此基础上, 应用SPSS软件对影响P2P网贷平台生存的4个主要因素构建Cox比例风险回归模型。在选择Cox模型变量的过程中, 采用逐步向前回归模型, 并适当放宽p值。当变量进入方程后, 若p<0.1, 则允许该变量进入最终方程; 相反, 若p>0.1, 则剔除该变量。

首先, 对全变量模型进行检验, 以判断方程中是否存在总体回归系数不为0的变量, 实验结果如表11所示。

表11 模型系数的综合测试

方法： 向前逐步回归(似然比)。

从表11可以得出, 模型整体检验的卡方值为19.591,p<0.01。因此, 在显著性水平为1%的条件下, 模型总体检验具有显著意义, 即至少存在1个自变量的总体回归系数不为0。据此建立相关方程, 经过逐步回归, 最终确定方程中变量如表12所示。

表12 最终确定方程中的变量

从表12可见, 结果显示筛选变量得到的最后模型只包括Userfunds变量,p=0.033, 具有显著意义。说明用户资金是否进行银行存管为影响P2P网贷“生存”或“死亡”的独立因素; exp(β)=0.012, 表明P2P监管平台用户资金是否进行银行存管对P2P网贷“生存”或“死亡”影响较大, 该指标统计意义为, P2P网贷平台将用户资金进行银行存管, 可将相对死亡概率降低至1.2%。

综上所述, 影响P2P网贷平台“生存”或“死亡”的最关键因素是用户资金是否进行银行存管, 相关函数分别如图3和图4所示。

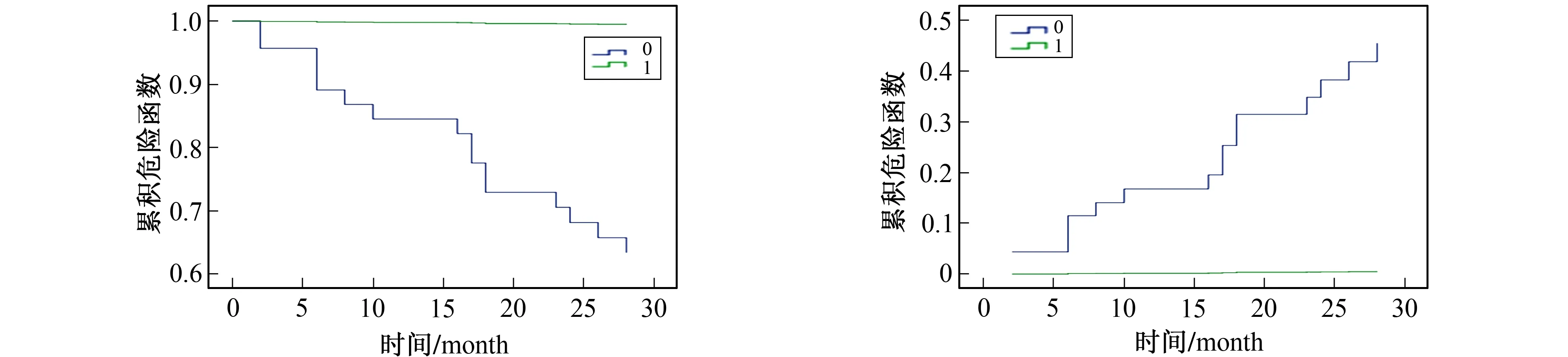
图3 累积生存函数 图4 累积危险函数 Fig.3 Cumulative survival function Fig.4 Cumulative hazard function

从图3和图4可知, 用户资金是否银行存管的P2P网贷平台生存函数和危险函数的对比效果非常明显, 用户资金进行银行存管的P2P网贷平台生存函数明显高于不存管的P2P网贷平台, 用户资金不进行银行存管的P2P平台的累积危险函数明显高于进行资金存管的P2P网贷平台。

6 结 语

笔者运用装袋法和随机森林对P2P网贷平台的变量进行初步筛选, 提取对其生存状影响较为重要的特征变量。在此基础上, 通过生存分析中的加速死亡模型和Cox比例风险回归模型对影响P2P平台经营状况的重要变量做进一步挖掘研究。

虽然在最初变量提取时, 平台的注册资本(以实际认缴为准)、 平台收益率、 上线时间和用户资金是否进行银行存管这4个变量均通过了Log Rank (Mantel-Cox)检验, 但通过拟合Cox比例风险回归模型向前逐步回归, 最终保留在模型里的变量只有用户资金是否进行银行存管一个独立变量, 从累积生存函数和累积危险函数可见, 该指标的取值对于P2P网贷平台“生存”和“死亡”有重要影响。从量化程度看, 用户资金进行银行存管可将死亡率降到1.2%。

结合实际分析, P2P网贷平台是否将用户资金进行银行存管在一定程度上影响着用户资金的安全。用户资金在银行存管, 可有效将P2P网贷平台与用户资金进行隔离, 也就是实现对P2P网贷平台的信息流和资金流的隔离, 即实现钱和交易的隔离, P2P网贷平台负责交易, 银行则负责相关交易中钱的流动, 避免有不法平台违规建立“资金池”。根据该结论的启示, P2P网贷用户在进行平台选择时不能只关注投资收益率, 即只关注自己可能获得的收益, 还应该关注平台的资金存管机制。这个指标决定着投资者投入平台资金的安全程度, 也为监管者提供依据, 应该加快建设P2P网贷平台资金的管理约束制度。