K-means算法聚类中心选取

张 朝, 郭秀娟, 张坤鹏

(1. 吉林大学 地球探测科学与技术学院, 长春 130026； 2. 吉林建筑大学 电气与计算机学院, 长春 130118)

0 引 言

K-means聚类算法是一种基于静态数据对象间相似度的动态硬聚类算法, 迄今人们已提出了众多可实行的改进算法[1-3], 并被广泛应用于不同领域。相比其他聚类算法,K-means聚类算法以其实现简单、 线性时间复杂度低的优势在数据科学和工业应用等领域被广泛采用。同时,K-means聚类算法也存在一些不足, 其包括： 无法自定聚类簇个数； 聚类结果随机性较大； 对初始聚类中心点存在很大的依赖性, 聚类结果受初始聚类中心影响较大, 导致聚类算法陷入局部最优解, 而非全局最优解[4-5]。为改善K-means算法存在的不足, 研究者试图从不同的角度对K-means算法进行改进, 如随机抽样、 距离优化和密度估计等方法[6]。

笔者在研究分析K-means初始聚类中心点选取的基础上, 提出了一种基于原始随机聚类中心点选取的并行选择机制, 以降低传统K-means聚类算法聚类结果对初始聚类中心点的依赖性, 避免传统算法下因随机初始化聚类中心点导致的聚类结果精确度不高问题, 提高聚类结果的准确性和稳定性。

1 K-means算法

1)K-means聚类算法的核心思想。K-means聚类算法的核心思想是：前期通过确定簇的个数K, 随机生成K个聚类中心点(centroids [1,2,…,k]), 将数据对象进行分类, 将n个数据对象分成k个簇, 簇间相似度极高, 簇与簇之间相似度较低。依据簇间数据对象到簇内聚类中心点的距离计算其相似度, 根据到各簇中心点的距离的不同将数据对象划分给不同簇。在处理庞大的数据集合时,K-means聚类算法相对其他算法效率更高。其时间复杂度为O(nkdt), 空间复杂度为O((n+k)d), 其中n为数据对象的数量,k为聚类簇数目,d为数据维度,t为迭代次数。通常情况下k≪n, 且t≪n。算法得到局部最优解。

2)K-means聚类算法分析。K-means聚类算法的聚类运算流程如下。首先, 随机选择K个聚类中心, 每个初始的聚类中心近似代表簇的平均欧几里德平均距离(Euclidean distance)或质心, 对于剩余的数据集, 进行欧氏距离运算, 生成距离矩阵, 并将其赋予对应矩阵中最接近的簇。然后, 重新计算每个簇的平均值, 在重复计算过程中, 准则函数实时变化, 直至准则函数收敛。

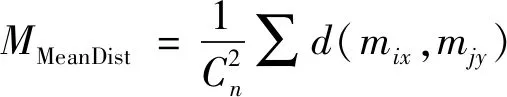
(1)

算法： 基于簇中数据集到簇中聚类中心点的距离(欧几里得距离)。

输入： 含有n个数据对象的数据集合D, 聚类生成的簇的个数k,D1∩D2∩…∩Dk=D。

输出：k个原始聚类中心。

2 聚类中心点的算法

K-means聚类算法对初始聚类中心点的选取采用随机选择的方法, 在对比不同距离算法过程中, 不同的距离算法选取的初始聚类中心存在较大差异, 合适的距离算法的选取和随机条件对后期的聚类实现会有较大的影响。

2.1 K-means聚类中心算法

初始聚类中心的选取采用随机选取机制, 在整个初始聚类中心点的选取过程中,K-means聚类算法提供了两种聚类点选择方式, 分别是中位数选择算法和算数平均值算法。初始聚类中心确定的算法不同, 对聚类效果存在不同程度的影响。聚类轮廓系数与初始聚类中心点的选择算法存在一定联系。

2.1.1 中位数算法

中位数(又称中值、 中点数或中数), 属于统计学中的专有名词。在数据集合中, 中数代表一个样本、 种群或概率分布的一个数值。根据这个数值将数据集合划分为上下等量的数据子集合。在有限的数据集合中, 可对数据对象进行排序观察, 按照升序或降序找出中位数。对数据集合按升序或降序排列后得到X1,X2,…,XN时, 当N为奇数时, 中位数为m0.5=X(N+1)/2； 当N为偶数时, 中位数为m0.5=(XN/2+XN/2+1)/2。

由于中位数不受数据集合中极端值的影响, 在一定程度上中位数对分布数据集合的代表性有所提升。但在离散型数据集合中, 如果数据集合中的偏态数据较多, 中位数则无法准确的代表该数据集合。

2.1.2 算数平均值算法

算数平均值(又称均值), 属于统计学中最基本、 最常用的一种平均指标。该均值算法主要适用于数值型数据集合, 不适用于品质型数据集合。算数平均值是加权平均数的一种形式(特殊在各项的权重相等)。

算数平均值简单易行、 反应敏捷、 确定严密等优点。但算数平均值极易受极端值影响, 在一定程度上极端数据会影响算数平均值的代表性[7]。极端数据对象数量过多会直接影响数据集合算数平均值的值。

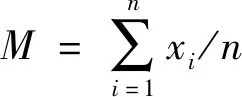
(2)

2.2 K-means聚类距离算法

K-means聚类算法初始聚类中心点是随机选取的, 但距离算法过程中有众多的选择, 具体距离算法有欧几里得距离(Euclidean distance)、 城市街区距离(City Block distance)、 皮尔森相关系数(Pearson correlation)、 绝对相关系数(absolute value of the correlation)、 非中心绝对相关系数(absolute uncentered correlation)、 斯皮尔曼等级相关系数(Spearman’s rank correlation)和等级相关系数(Kendall’s tau)等。

2.2.1 欧几里得距离算法

欧几里得距离(又称欧氏距离、 欧几里得度量)算法是聚类距离算法中较为常用的一种算法, 欧几里得度量(Euclidean metric)对数据对象进行计算, 依据数据点距离聚类中心点C1,C2,…,Ck的欧几里得距离进行分类, 确定距离点所属簇类。该算法的时间复杂度为O(nkdt)。计算公式如下。

二维空间计算公式

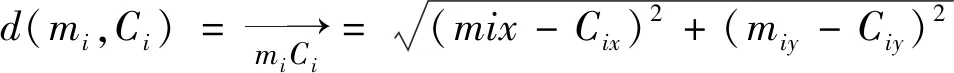
(3)

三维空间计算公式

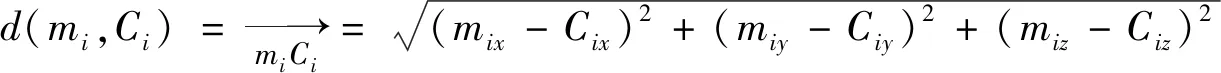
(4)

2.2.2 城市街区距离算法

城市街区距离(又称曼哈顿距离)源于城市区块距离, 是将多个维度上的距离进行求和后的结果, 是由赫尔曼·闵可夫斯基在十九世纪所提出的词汇。计算公式如下

d(i,j)=|Xi-Xj|+|Yi-Yj|

(5)

城市街区距离算法具有下列性质。

1) 非负性。d(i,j)≥0, 距离是一个非负的数值。

2) 同一性。d(i,i)=0, 对象到自身的距离为0。

3) 对称性。d(i,j)=d(j,i), 距离是一个对称函数。

4) 三角不等式。d(i,j)≤d(i,k)+d(k,j), 从对象i到对象j的直接距离不会大于途经的任何其他对象k的距离。

3 聚类中心点实验

笔者的实验环境为： Intel Core i5-2450m, DDR3 1333Mhz 4 GByte内存, 128 GB固态硬盘, Ubuntu操作系统, 利用Python3.5语言进行编程, 以验证算法的有效性。引用中国气象数据网天气数据, 截取同一天国内2 239座城市中106个城市的气象信息, 每条数据包含7个属性, 分为5类。分别对数据使用欧几里得距离算法和城市街区算法随机进行了10次测试, 记录其运行时间与轮廓系数, 并进行了综合比对分析。

3.1 实验方法

在实验过程中, 对数据集合进行了10次聚类实验。实验数据分析阶段引入轮廓系数[8]对聚类结果进行评价分析, 相同数据集合的前提条件下, 选用方法不同聚类效果不尽相同, 轮廓系数可以直接有效的反应聚类效果的好坏[9]。对于单一数据对象, 其轮廓系数计算公式如下

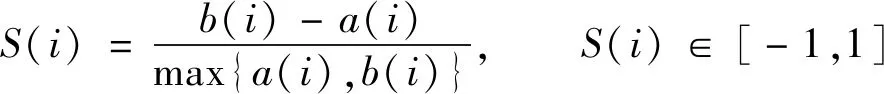
(6)

其中a(i)为该数据对象到本身所属簇内其他点的平均距离,b(i)为改数据对象到非本身所在簇的点的平均距离。当簇内有且仅有一个数据对象时, 定义S(i)为0[10]。轮廓系数的取值范围为-1～1, 轮廓系数越高表明簇内聚度和分离度都相对较优。

3.2 实验结果

为了检验聚类的有效性, 在众多距离算法中选取欧氏距离算法和城市街区距离算法, 其余距离算法因平均聚类轮廓系数为负, 不进行比较分析说明。确定数据集合进行聚类的K值为5。数据集合共有106条数据对象, 分为5类, 在实验过程中根据指定的初始聚类中心选取算法随机选取初始聚类中心和聚类距离算法进行距离度量计算, 对数据对象进行聚类分析。

在整个聚类实验过程中, 首先采用中位数初始聚类中心选取算法, 距离度量计算依次使用欧氏距离算法和城市街区距离算法, 对输出数据进行有效性记录。在系统性的进行测试实验过程中, 由于多次出现实验结果完全相同的情况, 故在多次循环测试过程中对重复性实验结果数据进行选择性舍弃。在对中位数初始聚类中心选取算法实验结束后, 改用算数平均值初始聚类中心选取算法, 距离度量计算依然延续使用首次实验中的欧氏距离算法和城市街区距离算法。进行实验分析, 记录相关数据结果。具体数据如表1所示。

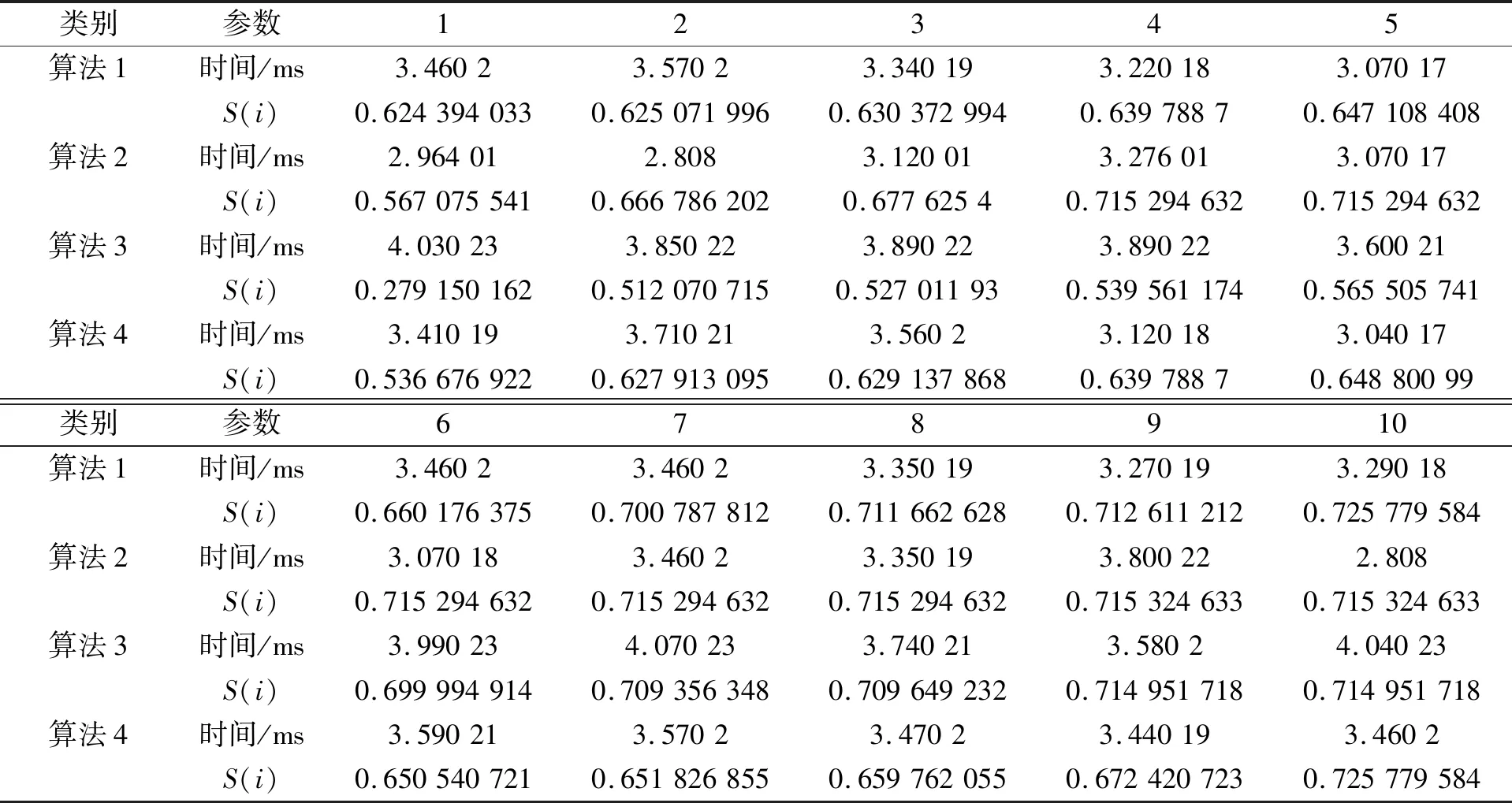
表1 组合算法运行时间及轮廓系数

图1 组合算法轮廓系数对比分析图Fig.1 Coefficient of combination algorithm outline contrast analysis diagram

在分析表1的时间参数和轮廓系数S(i)过程中, 发现在选择中位数初始聚类中心选取算法的前提下, 欧氏距离算法聚类效果远优于城市街区距离算法； 在选择算数平均值初始聚类中心选取算法的前提下, 欧氏距离算法聚类效果远优于城市街区距离算法。对表1中的4种组合算法的聚类结果的轮廓系数计算, 分别计算4种组合算的平均绝对偏差, 算法1的平均绝对偏差为0.035 947 948； 算法2的平均绝对偏差为0.032 819 146； 算法3的平均绝对偏差为0.112 560 421； 算法4的平均绝对偏差为0.028 708 484。

在分析表1的数据后, 提取4种组合算法的聚类轮廓系数进行比对分析, 如图1所示, 4种组合算法的轮廓系数曲线。

3.3 实验分析

通过对比4种组合算法对同一数据集合的聚类运算结果, 发现传统K-means聚类算法在随机选取初始聚类中心的过程中选取算法不同, 以及距离度量算法的不同对聚类效果有较大的影响。初始聚类中心算法与距离度量算法的不同组合, 对数据的聚类效果也不尽相同。组成的4种组合聚类算法在对数据进行聚类分析的过程中, 通过对其聚类轮廓系数的分析比较可以看出, 不同的算法组合其轮廓系数离散程度不同。

在考虑极端轮廓系数的前提条件下, 聚类离散程度最小的为欧氏距离算数平均值初始聚类中心选择算法, 而对应的离散程度最大的为城市街区距离算法中位数初始聚类中心点选择算法。

在忽略极端聚类轮廓系数的前提条件下, 欧氏距离算法中位数初始聚类中心点选择算法聚类效果最优, 在针对大数据聚类分析过程中在不考虑时间因素的前提下优先选择欧氏距离算法, 搭配的初始聚类中心选择算法算数平均值算法和中位数算法均可达到较好的聚类效果。

4 结 语

K-means聚类算法是科学计算、 数据分析、 数据挖掘中的重要算法之一, 通常作为经典的无监督机器学习算法[11]。笔者通过对比分析传统K-means聚类算法中的距离选择算法和初始聚类中心点选择算法, 在实际的数据聚类过程中, 进行相关实验, 通过聚类结果的轮廓系数, 初步确定了基于原始K-means聚类算法的优化K-means聚类算法。通过实验分析在可接受运行时间内, 重组后的K-means聚类算法稳定性更好, 准确性更高。