基于高斯学习多峰延迟粒子群优化算法

康朝海, 王思琪, 任伟建, 王博宇

(1. 东北石油大学 电气信息工程学院, 黑龙江 大庆 163318； 2. 本田技研科技有限公司 技术三部, 广州 510760)

0 引 言

标准粒子群在解决复杂的多峰函数时容易陷入局部最优值[1], 从而限制了PSO(Particle Swarm Optimization)的广泛应用。因此, 加快收敛速度和避免局部最优成为PSO研究中最重要也是最有吸引力的两个目标。虽然现有研究已提出了许多变体PSO算法分别实现这两个目标[1-4], 但很难同时实现这两个目标。例如, 文献[1]的综合学习PSO(Comprehensive-Learning PSO)着重于避免局部最优, 但由此导致收敛速度变慢。为同时实现这两个目标, 笔者通过引入高斯学习提高算法收敛速度。在此基础上, 根据粒子分布特征进行进化状态估计, 然后针对4种状态引入延迟因子避免局部最优。对单峰多峰函数的仿真实验表明, 改进的混合算法提高了收敛速度, 同时增强了粒子逃脱局部最优的能力。

1 粒子群优化算法

1.1 粒子群算法原理

PSO方法是受到鸟群觅食的启发所提出的模型。粒子种群个体视为无质量无体积的粒子, 粒子在搜索空间内运动, 其运动过程是一个社会学习和自我学习的过程, 在学习过程中不断对自己的搜索方向及搜索速度进行调整。

粒子群[5]中每个粒子i在搜索空间进行搜索时要考虑两个重要的向量, 即速度向量和位置向量。在进化迭代过程中, 粒子i按照下式运动

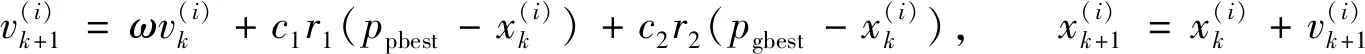
(1)

1.2 粒子群的研究现状

粒子群算法由于其简单高效而得到广泛应用。目前众多学者已提出了各种方法提高PSO的寻优能力[6]。两个较为突出的改进方法分别是调节算法参数和结合辅助搜索算子。其中, 合理权衡全局搜索和局部搜索可为找到最优解提供有效的帮助, Shi等[7-9]将惯性权重的概念引入标准粒子群算法中, 提出ω线性递减, 迭代生成惯性权重

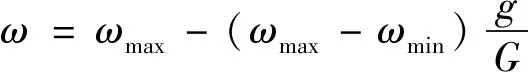
(2)

其中ωmin为惯性权重初值；ωmax为惯性权重终值；g为当前迭代次数；G为最大迭代次数。

较大的惯性权重会使PSO偏向于全局搜寻, 而较小的惯性权重偏向于局部搜寻[10]。因此,ωmin和ωmax通常分别设定为0.9和0.4。此外, 文献[11]已提出了PSO-TVAC(PSO with Time-Vary Acceleration Coefficients), 算法如下

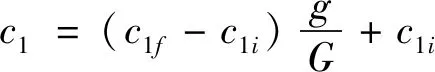
(3)

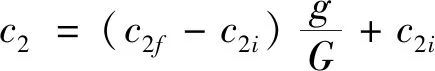
(4)

其中c1i、c1f、c2i和c2f为常数。

Zhan等[12]提出了一种自适应PSO(Adaptive-Particle-Swarm-Optimization)算法, 引入了一个进化因子(EF: Evolutionary Factor)量化平均距离(全局最佳粒子和其他粒子之间的距离)。根据进化因素, 通过一系列模糊隶属函数, 定义了4种状态, 即探索状态、 开发状态、 收敛状态和跳出状态。这4种状态已被用于每次迭代中自适应地控制惯性权重和加速度系数。Tang等[13]提出了一种SPSO(Switching PSO)算法, 克服了文献[12]算法的缺点。马尔可夫链根据进化因子决定的当前形态预测下一个形态, 且速度更新规则根据进化状态更新为另一种模式。

2 高斯学习策略

笔者在已有的高斯学习[14-15]基础上进行改进, 调整高斯学习的调用时机和适用个体。当全局最优值连续3代无变化时, 对全局最优个体和本次迭代中最优的前10%个体进行高斯学习, 在扩大学习对象的同时降低多次学习对整体算法运行速度的影响。

高斯学习是以引入高斯分布为基础, 从原有的最优个体随机选取某一维加上一个高斯随机扰动项, 其他维度保持不变, 从而获得一个新个体。若新个体适应度值优于原个体, 则保留新个体； 否则不保留。其学习方式为

Pd=Pd+(Xmax-Xmin)G(μ,σ2)

(5)

d=r(1,D)

(6)

其中P为当前最优个体的位置；d为该个体的一个随机维度；Xmax和Xmin为维度分量的上界和下界；G(μ,σ2)是服从高斯分布N(μ,δ2)的随机数,μ为高斯分布的均值；σ2为高斯分布的方差；r(1,D)为产生1～D之间的随机整数, 其中D为总维数。

为了提高算法的收敛速度, 将高斯学习策略[16]引入标准粒子群中, 对6种标准测试函数进行Matlab仿真, 结果证明收敛速度较标准粒子群算法快。

3 基于高斯学习多峰延迟粒子群优化算法

粒子群算法是基于种群的迭代算法, 在解决复杂的多峰函数问题时, 为具备更好的全局搜寻能力, 笔者在之前演化状态估计ESE(Evolutionary State Estimation)技术[17-18]中引入高斯学习, 并在粒子群速度公式上加入延迟因子, 有效地避免局部最优并且提高收敛速度。通过评价每次迭代的进化因子, 根据粒子群的间隔对进化状态进行分类。然后, 根据进化状态, 速度更新模型将从一种模式切换到另一种模式。此外, 为减少局部陷阱现象并扩大搜索空间, 将多峰延迟信息添加到速度更新模型中。

3.1 粒子群的进化状态估计

由文献[12]可知, 在PSO过程中, 粒子分布特征不仅随迭代次数变化, 而且随进化状态变化。例如, 在早期阶段, 粒子可能散布在各个区域, 因此粒子是分散的。然而, 随着演化过程的继续, 粒子将聚集在一起并聚合到局部或全局优化区域, 因此粒子分布信息与早期的信息不同。

根据搜索过程中的进化因子, 收敛状态、 开发状态、 探索状态和跳出状态分别用S1,S2,S3,S4表示。种群中第i个粒子和其他粒子之间的平均距离

(7)

其中M为群体大小；D为粒子维数。因此, 进化因子

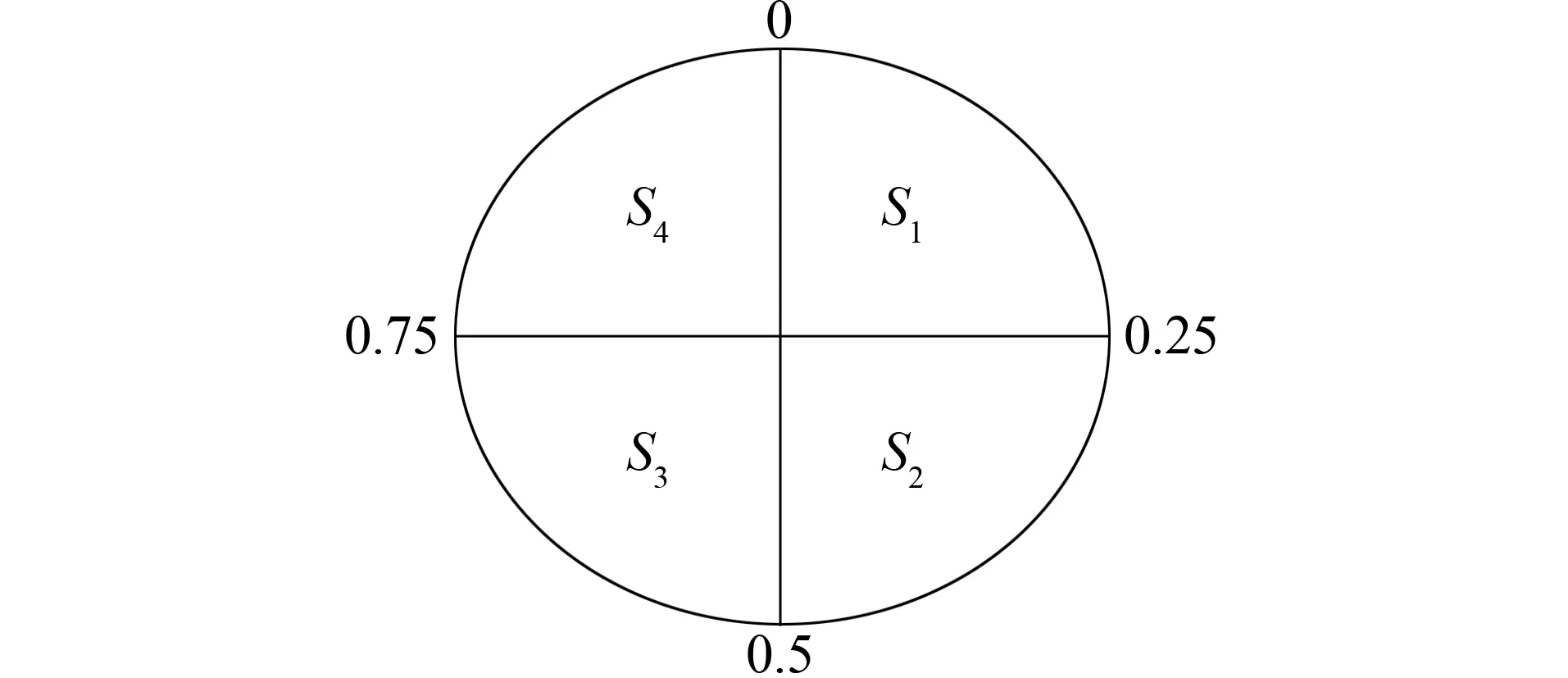
图1 状态分配图Fig.1 State assignment

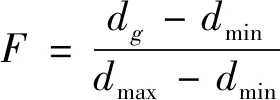
(8)

其中dg为全局最优粒子与群体其他粒子之间的平均距离；dmax和dmin分别为种群中di的最大值和最小值。进化状态根据进化因子由一系列模糊函数进行分类, 根据马尔可夫链, 等式分割策略用文献[19-20]中的状态预测对进化状态分类。进化状态估计利用粒子分布和相对粒子适应性的形成, 在状态的过渡期采用单例方法进行最终分类, 4种状态分配图如图1所示。

进化状态

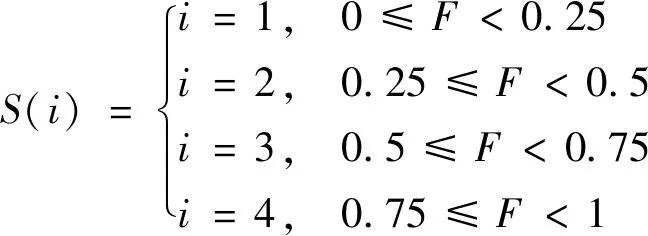
(9)

3.2 多峰延迟粒子群策略

为进一步提高粒子群算法的搜索能力, 文献[13]提出了切换PSO算法(SPSO), 其速度方程由马尔科夫链确定, 将马尔可夫跳跃参数引入速度和位置的更新方程中, 其更新方式为

vi(k+1)=ω(k)vi(k)+c1(Si(k))r1j(k)(pi(k)-xi(k))+

c2(Si(k))r2j(k)(pg(k)-xi(k)),xi(k+1)=xi(k)+vi(k+1)

(10)

其中c1(Si(k))和c2(Si(k))为加速度系数；j(k)为马尔科夫跳跃参数；pi(k)为粒子建立的最佳位置；pg(k)为整个群体中最好的位置。

然而, PSO算法还有一定的空间用于增强其摆脱早熟收敛的能力, 文献[21]提出了具有延迟信息的切换延迟PSO算法(Switching delayed PSO),不仅可改善全局搜索, 还可增强快速到达gbest的能力。此算法的速度和位置方程为

vi(k+1)=ω(k)vi(k)+c1(Si(k))r1(pi(k-τ1(Si(k)))-xi(k))+

c2(Si(k))r2(pg(k-τ2(Si(k)))-xi(k)),xi(k+1)=xi(k)+vi(k+1)

(11)

其中常数τ1(Si(k))和τ2(Si(k))为延迟因子。

为更彻底搜索整个空间, 文献[22]提出了多模延迟粒子群策略, 在新的学习策略中, 使用MDPSO(Multimodal Delayed PSO)算法, 其位置和速度更新式为

vi(k+1)=ωvi(k)+c1r1(pi(k)-xi(k))+c2r2(pg(k)-xi(k))+

si(k)c3r3(pi(k-τi(k))-xi(k))

+sg(k)c4r4(pg(k-τg(k))-xi(k))xi(k+1)=xi(k)+vi(k+1)

(12)

其中τi(k)和τg(k)分别为局部和全局延迟最佳粒子在[0,k]中均匀分布的随机延迟；ri(i=1,2,3,4)是[0,1]中的随机均匀分布数;si(k)和sg(k)是速度更新模型中新增项的强度因子, 其值取决于进化因子[21], 并按照如下方式设置。

1) 收敛状态S1： 群体中的粒子有望尽快地飞入全局最优点附近的区域。因此, 速度更新模型中省略延迟信息, 即将si(k)和sg(k)都设置为零。

2) 开发状态S2： 群中的粒子容易陷入局部最佳粒子周围的区域。因此, 局部延迟信息被加入到速度更新模型中, 即在强度因子si(k)=S2(k)的情况下, 随机选择先前迭代中的局部最佳粒子用于速度更新。

3) 探索状态S3： 尽可能多地搜索最优值很重要。因此, 为了更彻底探索整个空间, 引进全局延迟信息, 即强度因子sg(k)=S3(k), 随机选择先前迭代中的全局最优粒子用于速度更新。

4) 跳出状态S4： 局部最佳粒子急于从局部最优点周围的区域跳出。因此, 要为这些粒子提供更多的能量从这个区域逃逸, 同时引进局部和全局延迟信息, 即强度因子si(k)=S4(k)和sg(k)=S4(k)。

由式(3)和式(4)可得：c1=c3和c2=c4。

3.3 改进算法步骤及流程图

多峰延迟粒子群策略虽然会对搜索空间进行彻底搜索并且更有可能获得全局最优, 但是该策略会略微降低收敛速度。由上述分析可知, 引入高斯学习策略可有效提高收敛速度。笔者在上述多峰延迟粒子群算法中引进改进高斯学习策略, 算法步骤如下。

Step1 初始化粒子群和算法参数。根据式(2)～式(4)计算出相应的ω和ci。

Step2 计算评估每个粒子的适应值, 更换pbest和gbest, 并将其留存为历史信息。

Step3 判断全局最优值是否连续3代无变化, 满足则根据式(5)和式(6)对全局最优值和本次迭代最优的前10%个体进行一次高斯学习。

Step4 在当前位置, 根据式(7)计算每个粒子i到所有其他粒子的平均距离di。

Step5 比较所有di并确定最大距离dmax和最小距离dmin。将全局最佳粒子di定义为dg。通过式(8)计算进化因子, 通过式(9)确定进化状态。

Step6 根据随机延迟τi(k)、τg(k)和强度因子si(k)、sg(k)的设置方式更新多峰延迟信息。

Step7 根据式(12), 更新粒子速度和位置。

Step8 判断是否达到最大迭代次数, 满足则输出全局最优值； 否则返回执行Step2。

算法流程图如图2所示。

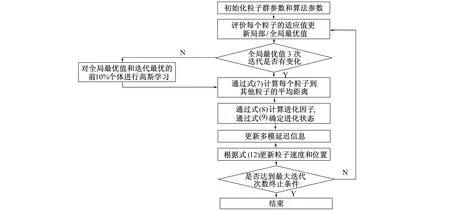
图2 算法流程图Fig.2 Algorithm flowchart

4 仿真实验

4.1 基准函数的配置

在下面的仿真实例中, 采用了一些常用的基准函数评估基于高斯学习多峰式延迟粒子群算法的性能。基准函数由方程式给出, 如表1所示。

表1 标准测试函数

表1中, 球函数f1(x)是典型单峰优化问题, 通常用于测验优化算法的收敛速度；由于Rosenbrock函数f2(x)很难获取全局最优, 它可看成多峰函数；f3(x)到f6(x)是其他典型单峰、 多峰函数, 它们都很难获取全局最优值。为此, 表1展示了基准函数的具体配置, 第4列是基准函数的最优值, 第5列是每个维度的搜索空间。

4.2 算法仿真

仿真采用表1的基准函数, 同时引入标准粒子群(PSO)算法进行对比, 对比图如图3所示。

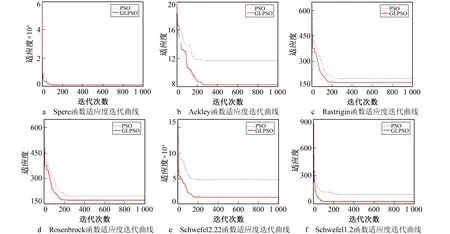
图3 标准函数适应度迭代曲线对比Fig.3 Comparison of standard function fitness value iteration curves

由图3可知, 改进的高斯学习可有效克服标准粒子群算法处理多峰的复杂问题时收敛速度慢的缺点。6个测试函数的仿真实验中, Ackley的测试效果改进最为明显, GLPSO收敛速度明显提高。

由上述仿真启发, 针对粒子群对多峰函数[23-24]寻优能力的问题, 引入改进的高斯学习提高算法收敛速度, 并在此基础上对4种进化状态加入延迟因子以避免陷入局部最优, 提出一种基于高斯学习的多峰延迟粒子群策略。

与此同时, 引入PSO-LDIW(Linearly Decreasing Ineria Weight)、 PSO-TVAC(Time-Vary Acceleration Coefficients)、 PSO-CK(Constriction Factor)、 SPSO和SD(Switching Delayed)PSO、 MD(Modified Discrete)PSO 6种相应标准的PSO算法与提出的GLMDPSO算法进行比较。参数设置如下： 种群S=20, 种群维数D=20, 最大迭代次数N=1 000。每个实验独立重复50次, 用于后续的统计分析。

4.3 仿真分析

上述PSO算法对每个基准函数的平均适应度曲线如图4所示, 其中水平坐标表示迭代次数, 垂直坐标的值用对数形式表示。

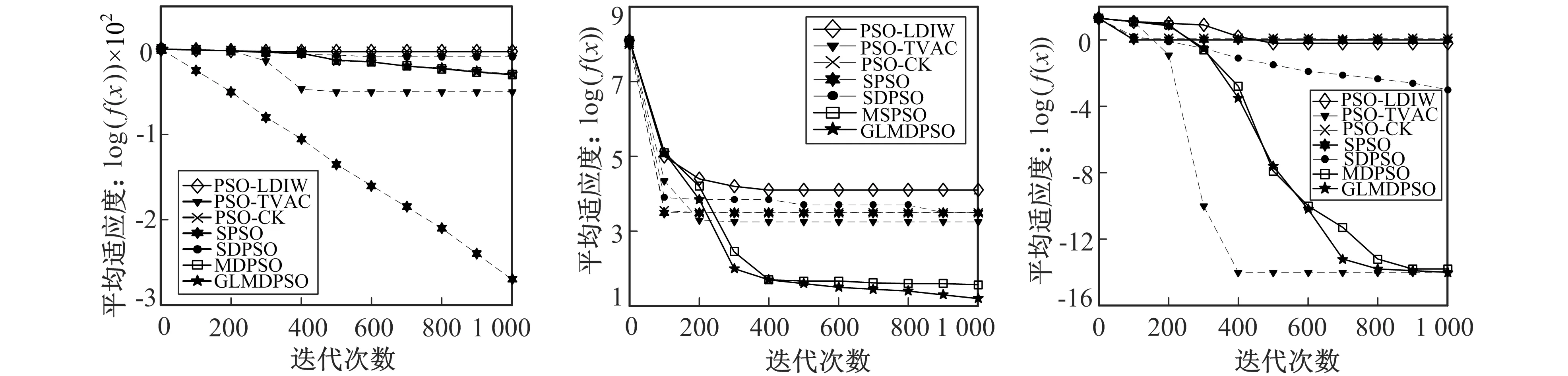
a Spere函数适应度对数迭代曲线 b Rosenbrock函数适应度对数迭代曲线 c Ackley函数适应度对数迭代曲线

d Rastrigin函数适应度对数迭代曲线 e Schwefel2.22函数适应度对数迭代曲线 f Schwefel1.2函数适应度对数迭代曲线图4 标准函数适应度值对数迭代曲线对比Fig.4 Comparison of logarithmic iterative curve of standard function fitness value

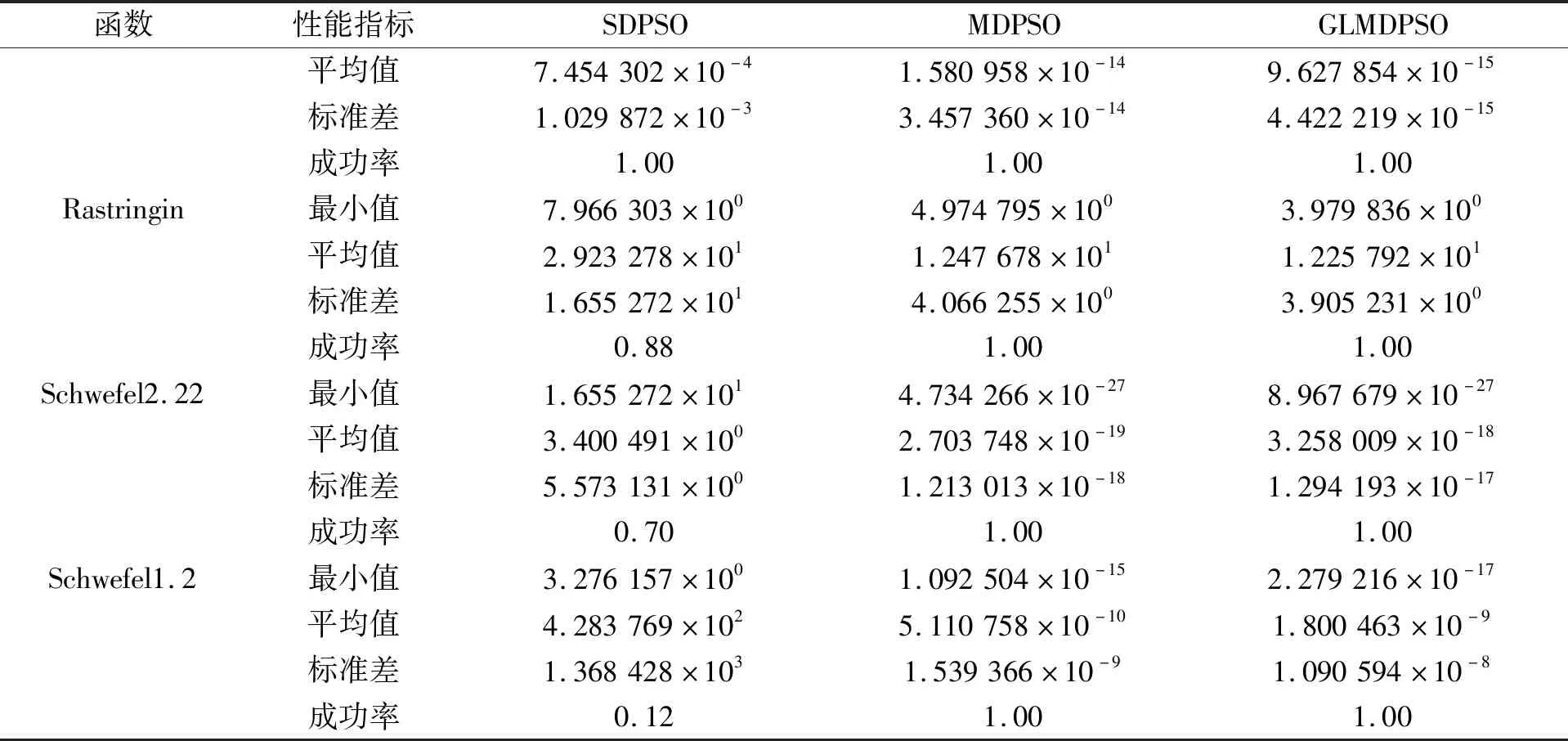
表2列出了各算法分别运行50次适应度的最小值、 平均值和标准差及每个算法对基准函数寻优的成功率。如表2所示, 一些算法对基准函数的优化成功率非常低, 即随着迭代的增加, 算法的最优解不会收敛到阈值以下, 因此它们和GLMDPSO算法相比, 平均值相差较大。GLMDPSO算法在Rosenbrock、 Ackley和Rastrigin基准函数上的寻优效果和收敛速度优于其他算法。在Sphere函数中, PSO-CK和SPSO收敛速度稍快。由图3和表2可知, GLMDPSO算法比其他算法具有更好的全局搜寻能力。由图3可以看出, GLMDPSO的收敛速度比MDPSO的收敛速度更快, GLMDPSO仿真时间为17.820 3 s, 而MDPSO仿真时间为20.786 s。即GLMDPSO具有更强搜寻能力的同时还弥补了MDPSO收敛速度慢的缺点。因此, 笔者提出的GLMDPSO算法在标准评价中优于其他PSO算法。

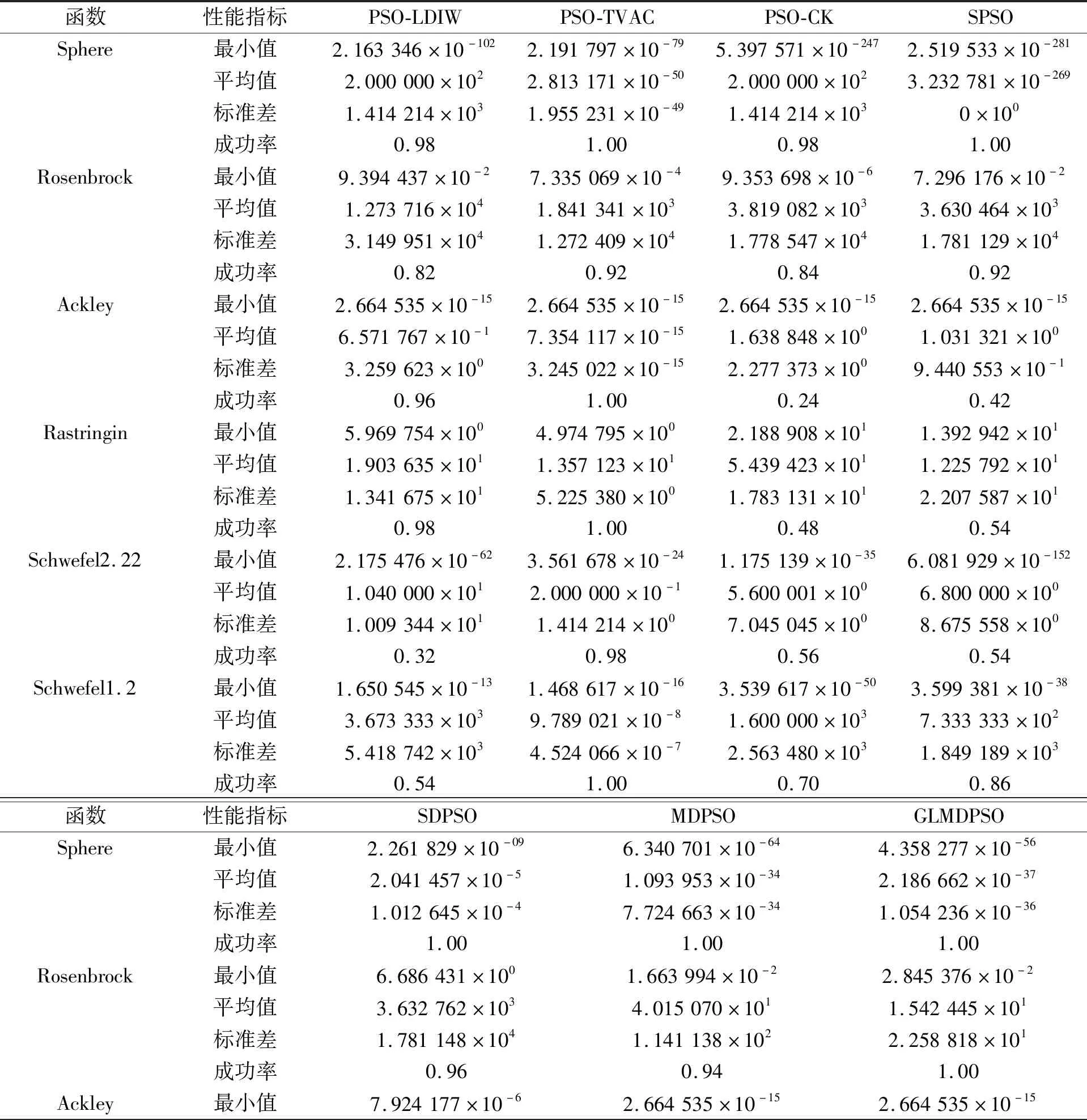
表2 7种算法在标准测试函数上的寻优结果比较

(续表2)

函数性能指标SDPSOMDPSOGLMDPSO平均值7.454302×10-41.580958×10-149.627854×10-15标准差1.029872×10-33.457360×10-144.422219×10-15成功率1.001.001.00Rastringin最小值7.966303×1004.974795×1003.979836×100平均值2.923278×1011.247678×1011.225792×101标准差1.655272×1014.066255×1003.905231×100成功率0.881.001.00Schwefel2.22最小值1.655272×1014.734266×10-278.967679×10-27平均值3.400491×1002.703748×10-193.258009×10-18标准差5.573131×1001.213013×10-181.294193×10-17成功率0.701.001.00Schwefel1.2最小值3.276157×1001.092504×10-152.279216×10-17平均值4.283769×1025.110758×10-101.800463×10-9标准差1.368428×1031.539366×10-91.090594×10-8成功率0.121.001.00

5 结 语

针对粒子群算法迭代最优值搜索停滞及收敛精度低的问题, 引入高斯学习, 有效地加快收敛速度, 解决了算法收敛慢、 精度低的问题。同时根据粒子群的进化状态估计, 采用基于改进高斯学习多峰延迟粒子群策略进一步提升全局和局部搜索能力。为了对比其他6种算法, 针对6个基准测试函数进行数值仿真实验, 实验结果证明了笔者算法可提高收敛速度, 同时保证良好的搜寻能力。