一“网”打“尽” 精准教学——以y=Asin(ωx+φ)的图象性质为例

李昌成 曾 静 车燕昭

(新疆乌鲁木齐市第八中学 830002)

三角函数的公式多，性质多，题型多，学生容易混淆出错.针对这种现状，本人在高三复课时采取了“集中歼灭”的策略开展教学，也就是老师先把公式、性质讲清楚，督促学生把公式、性质记牢固并理解，然后集中应用，对比学习，区别对待，达到掌握的目的.现举一例，以飨读者.

题目已知f(x)=2(cos2x+sinxcosx)，

(1)求f(x)的最小正周期；

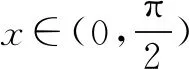
(3)求f(x)的单调递增区间；

(4)求f(x)图象的对称轴方程；

(5)求f(x)图象的对称中心；

(6)解不等式f(x)>1；

(7)y=sinx的图象经过怎样的变换，能变成f(x)的图象？

(8)f(x)是偶函数吗？若不是，怎样变换可以使其成为偶函数？

(9)在△ABC中，f(A)=2，BC=2，求△ABC的面积的最大值.

注:这里练习了二倍角公式、扩角降幂公式、辅助角公式等重要的三角公式.公式只有用在应用中才能记牢用活，才能进一步地理解它们的内在联系.

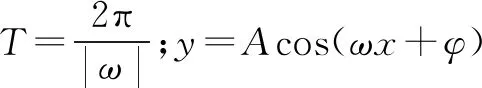
注:本问凸显了函数中定义域优先的要求，也反映了三角函数整体非单调的特性，这是很多学生容易忽视的.

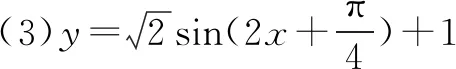
注:本问巩固了y=Asin(ωx+φ)的单增区间的求法，还可以进一步回顾该函数单减区间怎么求？限定定义域的单调区间怎么求？y=Acos(ωx+φ)、y=Atan(ωx+φ)的单调区间怎么求？还有若A<0，该注意什么？这些问题不复杂，但是重要，必须全面总结，不可疏漏，分类掌握.

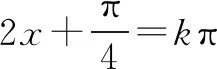
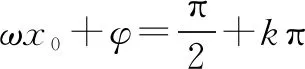
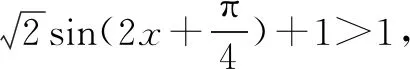
注:解三角不等式可以利用三角函数图象取解集，一般要求在一个周期内的图象连续即可.也可利用三角函数线取解集.

注:三角函数图象变换通常有两种方式：

①先做相位变换，再做周期变换，再做振幅变换，最后上下平移，即：y=sinx→y=sin(x+φ)→y=sin(ωx+φ)→y=Asin(ωx+φ)→y=Asin(ωx+φ)+k;

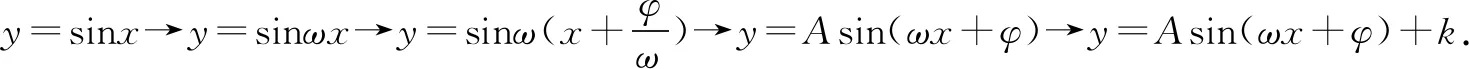
注:这类因平移导致奇偶性变换的问题要紧紧依靠诱导公式实现目的.解题依据是：f(x)=Asinωx、f(x)=Atanωx是奇函数，f(x)=Acosωx是偶函数.

由均值不等式得AB2+AC2≥2AB·AC②.

注：三角函数图象性质与解斜三角形有机结合实现了学以致用的教学目的，在高考中此类题型以解答题出现，注意准确使用正弦定理、余弦定理、面积公式、诱导公式、均值不等式等知识.

通过这一题，我们巩固加深了对三角公式、三角函数的定义域、值域、单调性、奇偶性、对称轴、对称中心等性质、图象变换规则以及解斜三角形的理解.各问题间既有区别，也有联系，在比较中促进知识升华，将零散的知识串成了一条线，学生的收获多多.这种一网打尽的教学案例很多，同仁可以尝试这种教学，避开题海战术.