巧建坐标系 妙解平抛问题
秦 黎
(浙江省绍兴市第一中学 312000)
学生在研究物体沿直线运动的问题时,通常能够正确进行受力分析,建立直角坐标系,然后解决问题.然而当学生遇到曲线运动时,由于物体的运动轨迹不在坐标系上,学生就会不知所措,不能正确的将速度和加速度分解到坐标系上,独立地考虑这两个方向上的分运动.
例1 如图1所示,一小球自倾角θ=37°的斜面顶端A以水平速度v0=20 m/s抛出,小球刚好落到斜面的底端B(空气阻力不计),求小球在平抛运动过程中离开斜面的最大高度h.
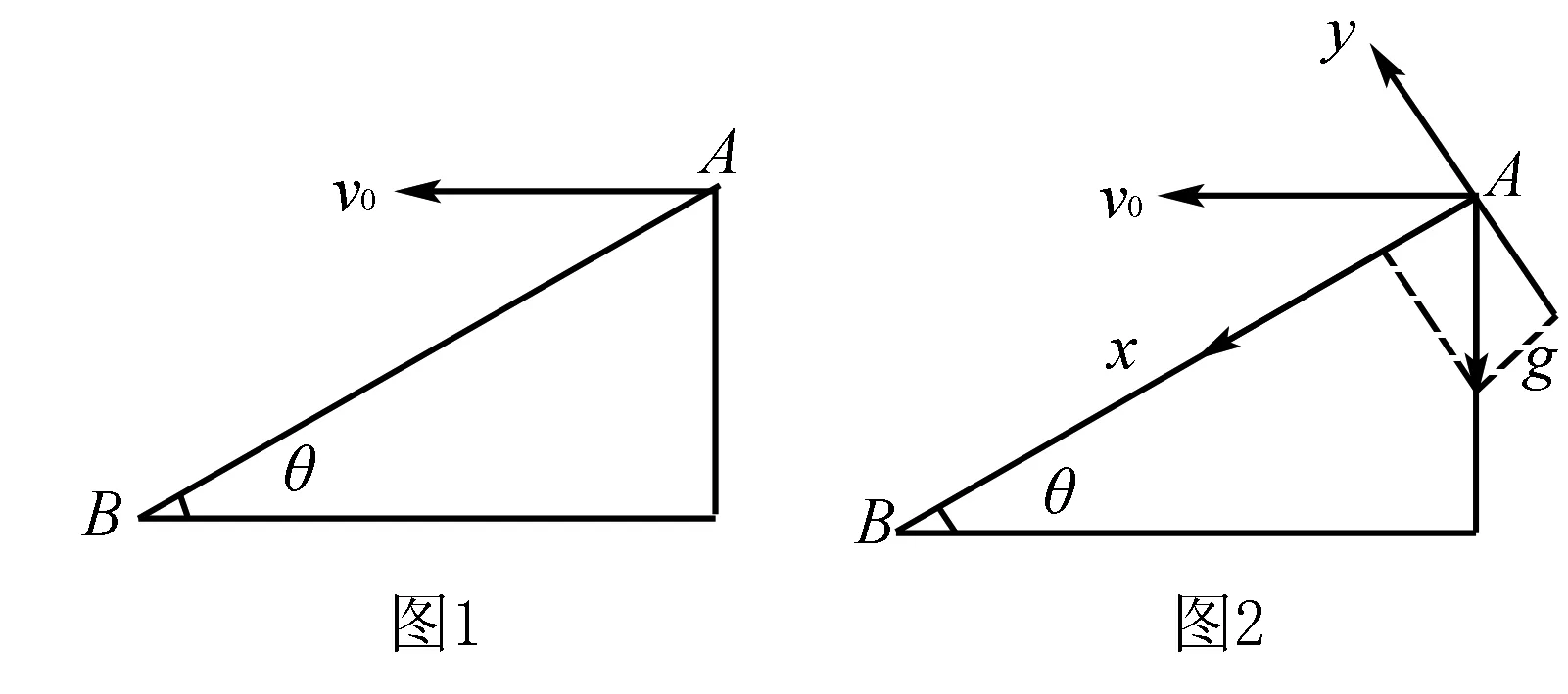
评析本题中,由于要求离开斜面的最大高度,所以可以建立如图2所示坐标系,将初速度v0和重力加速度g分别进行分解,则在x轴和y轴方向分别独立地做匀变速直线运动.在y轴方向,vy=0时,物体在y轴方向的分位移最大,实际运动的轨迹距离斜面最远.
根据(v0sinθ)2=2gcosθ·h可以求得距离斜面的最大高度.
例2一斜面倾角为θ,A、B两个小球均以水平初速度v0水平抛出,如图3所示.A球垂直撞在斜面上,B球落到斜面上的位移最短,不计空气阻力,则A、B两个小球下落时间tA与tB之间的关系为( ).
A.tA=tBB.tA=2tB
C.tB=2tAD.无法确定
评析该题目可以根据斜面倾角的正切值法求解落在斜面上的平抛运动相关问题,但较为繁琐.如果学生能够巧妙建立坐标系,发散思维,将会使题目简化,让学生豁然开朗.
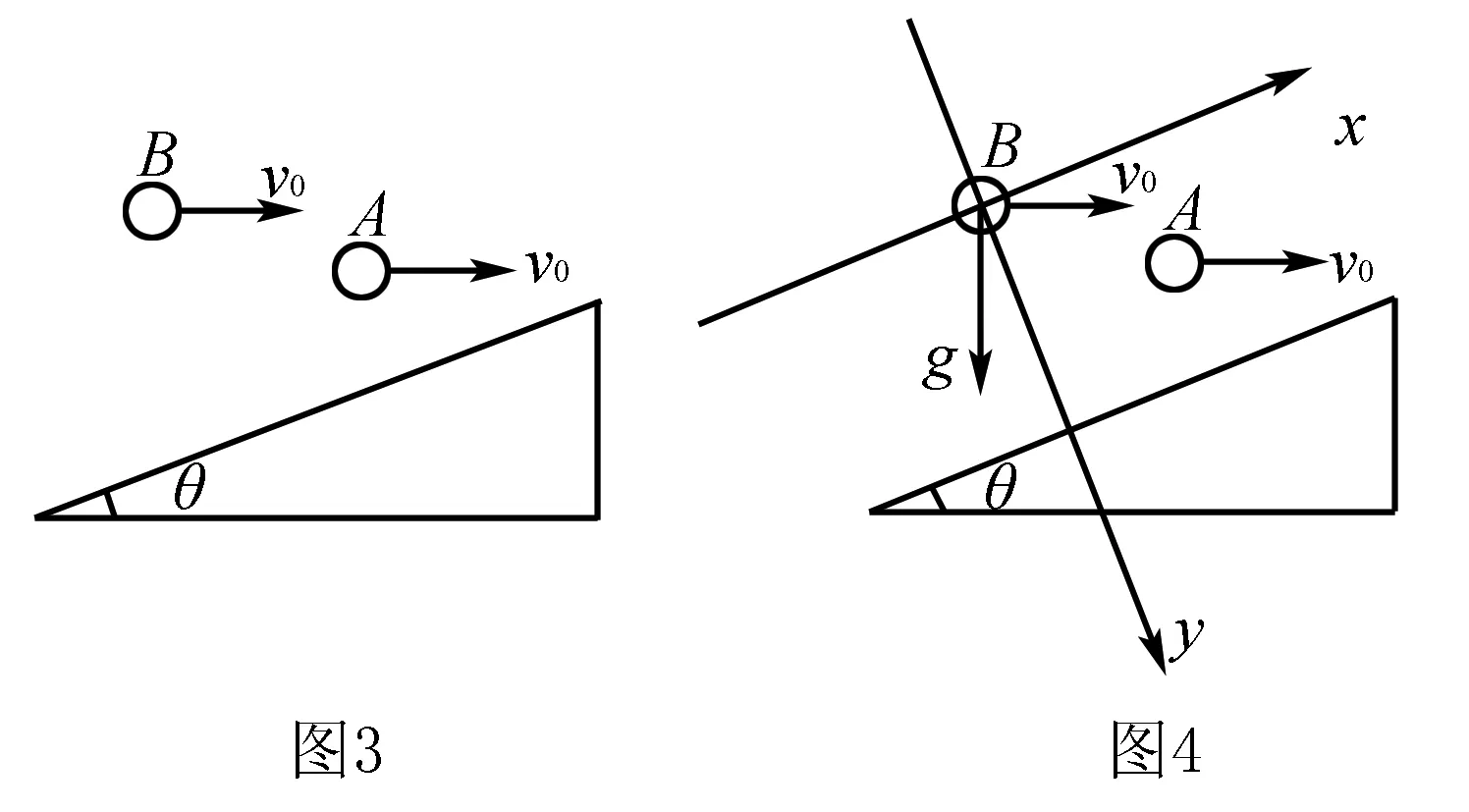
由题意,B球落到斜面上的位移最短,说明B的位移方向垂直于斜面.以此对B球建立如图4所示坐标系,将B的初速度v0和加速度g分解到x轴
则B球沿着x轴方向位移为零:
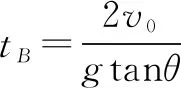
由于A球垂直撞在斜面,将A的初速度v0和加速度g分解到x轴所以x轴方向的分速度为零,即
0=v0cosθ-gsinθ·tA
所以tB=2tA
例3 如图5所示倾角为37°的光滑斜面上,一小物块从距离地面高度为6.25m处静止下滑,一个半径R=2.5m的光滑圆轨道同时与斜面和地面相切,问:
(1)小物块能否到达圆轨道的最高点
(2)求小物块从最高点平抛后到撞击斜面所用时间
评析第(1)问答案:小物体恰能到达圆轨道的最高点,最高点的水平速度为5m/s.解析略
第(2)问,小物块从到达最高点开始做平抛运动,由于撞击斜面时速度大小和方向不详,小物体撞击斜面的位置也不详.如果该题改变斜面倾角,或者改变小物体初始高度,那么问题更具有一般性.学生针对这类问题,往往束手无策.如果能巧妙建立坐标系,以不变应万变,那么不管多么复杂的运动,都能够迎刃而解.
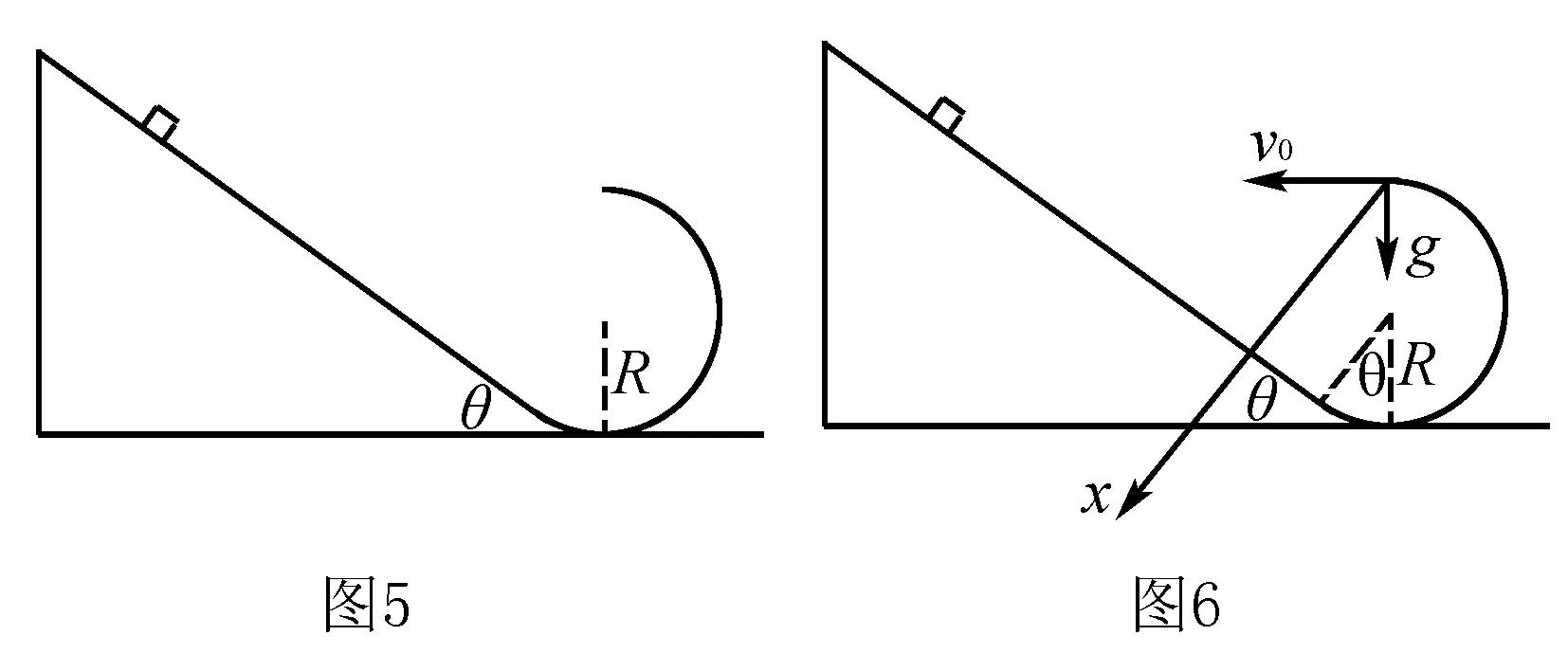
如图6所示,以最高点为原点,垂直于斜面向下建立一维坐标系.将水平速度v0和g分解到x轴.则小物块无论水平速度有多大,在x轴方向做的都是匀加速直线运动,根据合运动与分运动的等时性,小物块撞击斜面的时间均与沿x轴方向运动到斜面的时间相等.
由几何关系位移x=R+Rcosθ
若改变条件,仍然可以采用此方法巧妙建立坐标系,得到最高点到撞击斜面的时间,以时间为突破口,此类问题就变得容易了.
综上所述,在解决平抛运动的问题时,巧妙建立坐标系,将速度和加速度进行分解,然后独立地解决各个方向的运动情况,思路清晰,行之有效,可以迅速解决较复杂的计算题,起到事倍功半的效果.笔者仅是从运动学的相关问题进行了例析,其他动力学的相关问题等也可以通过巧妙建立坐标系,另辟蹊径.

