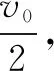电容综合问题中的短暂过程与持续过程

陶汉斌

(浙江省金华第一中学 321015)

一、RC电路的一般特征

当uc=E时，i=0，充电过程结束.试验证明，充电过程可用下面公式进行描述，即

从公式中不难看出，充电过程中uc和i是按指数规律变化的，而充电的快慢取决于电阻和电容的乘积，因此称RC为时间常数τ，即τ=RC.如果R和C的单位取欧姆和法拉，则τ的单位为秒.从中可以看出，τ越大充电越慢.当t=3τ时，uc=0.95E，当t=5τ时，uc=0.993E.一般认为当t=3τ～5τ时，电容器上的电荷已被充满.我们可用图2所示的图线来直观理解电容器充电过程中电流与时间的关系.

当t=4τ～5τ时，工程上即认为电容的初始储能已被全部消耗，也就是放电完毕.其放电过程的中电流与时间的关系与如图2相仿.

当然，如果当开关打接到a充电时电容器的初始电压uc不为零，那么充放电过程的公式将更加复杂，在这里就不进行讨论了.

二、理解短暂过程与持续过程

在RC电路中，充放电的快慢取决于电阻和电容的乘积，因此称RC为时间常数τ.当t=5τ时电容器充放电基本完成，那么这个5τ时间能否理解为“瞬间”的短暂过程呢？还是应该理解为一个较长的持续过程呢？

我们可以设想在12V电源上充电，理想状态电池没有内阻，连接的导线也没有电阻，τ=RC=0，充电时间等于0，瞬间电流无穷大，这当然就应该理解为“瞬间”的短暂充电过程.同理如果电容器放电的过程中电路中的所有电阻都可忽略不计，比如用一根足够强度的金属丝，直接短路电容器两端使它放电，则由于金属丝长度很短，电阻很小，造成短路电流很大，电容器储存的电荷瞬间被释放完毕，这也是“瞬间”的短暂放电过程.

在实际的电路中肯定存在一定的电阻，比如整个电路的等效电阻为1Ω，电容器的电容为1000uF，时间常数τ=RC=1ms，充放电的时间可认为就是5τ=5ms，这个过程就可理解为较长的持续过程.如果我们将电容器换成1F的超级电容，那么时间常数τ=RC=1s，充放电的时间就是5τ=5s，这应该是一个相当的长的持续过程了.这种短暂过程与持续过程，在经典力学中涉及动量守恒问题时也常常有这两种过程的分析.

三、典型错例欣赏

(1)导体棒获得初速度v0时，电容器的带电量；

(2)导体棒上滑过程中加速度的大小

(3)求导体棒从最高点滑到低端的时间.

解析本题从力与能量两个角度分析电磁感应现象，根据法拉第电磁感应定律、欧姆定律和电流的定义式推导出电流与加速度的关系是解题的关键.对于第2小题导体棒切割类型，关键要正确受力分析，把握其运动情况和能量转化关系.

(1)【雾里看花】

当导体棒获得初速度v0时将产生感应电动势，电容器的电压等于此时导体棒切割磁感线产生感的应电动势，即

U=E=BLv0

此时电容器的带电量为

q=CU=CBLv0

【正本清源】 由于电容与导体构成的回路中，整个回路的电阻为0，电容器初始电压为0，电容器充电的过程是一个短暂的过程.在这个短暂的过程中，导体棒的电流为无穷大，它将受到很大的安培力作用(此时重力可忽略)，在瞬间安培力的作用下导体棒的速度发生突变而位置不变，这类似经典力学中的瞬间碰撞过程.我们可在这个短暂的过程对棒应用动量定理

-BiL·Δt=mv-mv0

而充电的电流

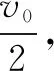
mgsinθ-F安=ma

又F安=BiL，

联立方程可解得

导体棒的运动是向上做匀减速运动的一个持续过程.

(3)【雾里看花】上滑过程中导体棒做匀减速运动，由运动学公式求出导体棒上滑的最大距离.对于下滑过程运用动量定理和积分法求导体棒的运动时间.

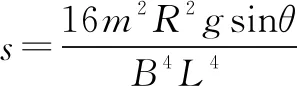
以最大速度匀速下滑时

导体棒下滑的过程中，由动量定理可得

mgsinθ·t1-I安=mv1-0

mgsinθ-F安=ma

所以开关打到a后做匀加速度直线运动

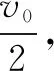
以最大速度匀速下滑时

解得最大速度为

导体棒下滑的过程中，由动量定理可得

mgsinθ·t1-I安=mv1-0

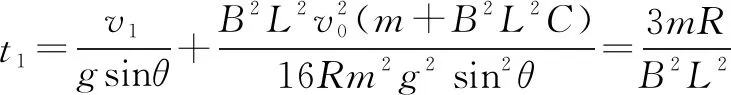
开关打到a时为瞬间的短暂过程，这个过程速度v1会发生突变，我们对这个短暂的过程对棒应用动量定理-BiL·Δt=mv2-mv1

此过程中电容器的充电量为q′=CBLv2

然后导体棒做匀加速度运动对电容器继续充电，根据牛顿第二定律mgsinθ-F安=ma

同样我们可解得

所以开关打到a之后的持续过程中，导体棒做匀加速度直线运动，由运动学公式