基于输入信号周期的一阶RC电路时间常数的测量方法研究
姜玉亭 杨建波 李晓冬
桂林电子科技大学电子电路国家级实验教学示范中心 广西 桂林 541004
0 引言
RC电路时间常数的测量是电路实验的重点实验项目,更是实验测量的难点,实验教学中通常采用间接法测量获得电路的时间常数。
RC电路时间常数的测量,实验中采用方波来模拟阶跃激励信号,实验原理图如图1所示。为了能够看到完全响应的波形,选择方波的周期要远远大于电路的时间常数τ(周期比电路的时间常数大5~10倍),这样就可以用示波器观察电路的响应波形,从而测量电路的时间常数。
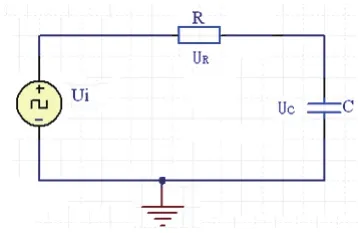
图1 方波作用下的RC串联实验电路图
1 RC电路时间常数测量的常规方法
RC一阶电路的零输入响应和零状态响应分别按指数规律衰减和增长,其变化的快慢决定于电路的时间常数τ0零状态响应时,
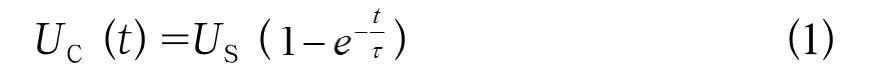
式中,τ=RC,UC(t)的曲线可以用示波器测量得到,US是输入信号的幅度,如果在UC(t)曲线上找到t=τ的点,即令t=τ,那么公式就变为:

公式(2)说明,在UC(t)曲线(即零状态曲线)上,电容电压由0值上升到电源电压US的0.632倍时所需的时间就是时间常数τ,如图2所示。
实验教学中,时间常数τ的测量关键是确定a点(图2中的点a)。使用KEYSIGHT 2000X数字示波器,将X1游标位于零状态响应曲线的最低点,调节X2游标,使得X2-X1的差值为0.632US,则X2游标与曲线的交点就是a点;将Y1游标位于曲线的起始点,移动Y2游标至a点,则Y2-Y1的差值即为时间常数τ。在测量时间常数时信号发生器的周期要调到合适的值,周期过小或过大都会增大实验误差。
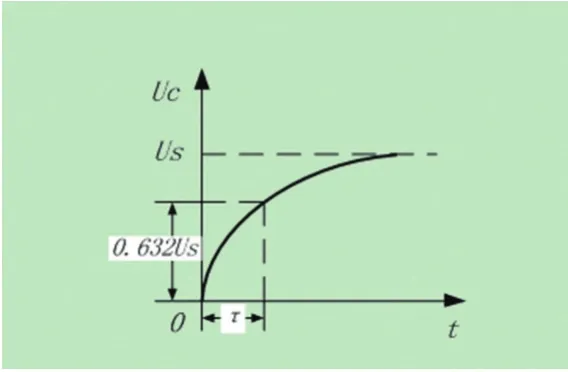
图2 RC电路零状态响应曲线及时间常数的测量
2 基于输入信号周期的RC电路时间常数的测量方法
假如输入信号的周期不足以使电容充满电和放完电,即电容经过半个周期充电后,还没有达到输入信号的幅度大小US就开始放电,再经过半个周期后还没有放完电又开始充电,如图3所示,如此反复。
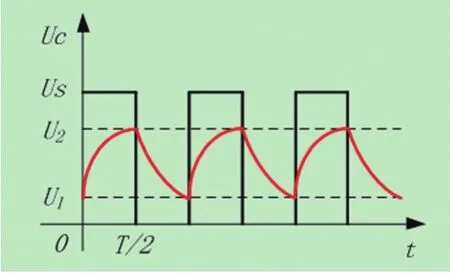
图3 RC电路电容充放电波形图
设一个周期内电容充电的初始值(电容放电的终值)为U1,电容充电的终值(电容放电的初始值)为U2,输入信号的周期为T,则充电方程为

电容充电的终值为
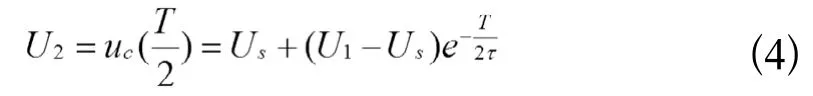
放电方程为

电容放电的终值

联立公式(4)、(6)得
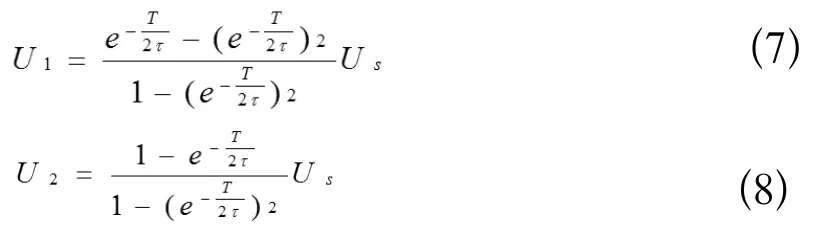

公式(9)说明,电路工作一定时间后,每个周期中电容电压的最大值U2和电容电压的最小值U1关于输入方波信号的平均电压值对称。
公式(8)-(7)得

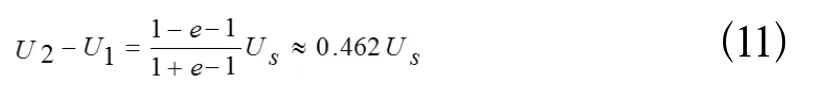
为此,我们导出了基于输入信号周期的RC电路时间常数的测量方法,即信号发生器的输入方波信号的幅度不变为US,改变输入信号的周期T,用示波器观察并跟踪电容电压的幅度,当电容电压的幅度UC减小到输入信号幅度Us的0.462倍时,此时T/2的时间即为时间常数τ。
3 实验数据测量及结果分析
按图1电路接线。电阻R为10kΩ,电容C为0.22μF,取方波信号的频率为2.5kHz,幅度Us为3V,此时的电容电压最大值UC(T/2)=Us。按常规方法,测得的电路时间常数τ约为23μs。输入方波的幅度Us为3V不变,减小输入方波信号的周期,用示波器追踪观察电容电压的波形,当电容电压的幅度减小到最大幅度的0.462倍时,此时的T/2约为21.8μs即为基于输入信号周期的电路时间常数测量法得到的电路时间常数τ,与理论值接近。
4 小结
常规法测量电路时间常数,要求电容电压在示波器上显示的波形尽量的宽,这样可以减小测量误差。基于输入信号周期的RC电路时间常数的测量方法,是利用电容电压幅度与输入方波信号幅度的特定比例关系而得到输入信号的周期与电路时间常数τ的关系,即。此方法操作简单方便,可以适当减少因常规方法确定a点的繁琐而造成的人为误差。
项目经费支持:2016年度广西高等教育本科教学改革工程项目“基于翻转课堂的建筑电气专业实验教学模式及支撑平台研究”2016JGA197
[1]邱关源,罗先觉.电路[M].北京:高等教育出版社,2006:140-152.
[2]李晓冬等.电路分析基础实验设计与应用教程[M]. 陕西:西安电子科技大学出版社,2016:95-106.
[3]黄贤群.RC 串联电路暂态过程时间常数的测量[J].实验室科学,2012(3):83-90.
[4]曹新亮,杨红霞,宋永东.测量一阶电路时间常数的实验方案探讨[J].延安大学学报,2005,24(1):61-62.

