轻杆双球模型问题的处理探索

张大洪

(重庆市潼南实验中学 402660)

一、例题解析

图1

A.下滑过程中A的机械能守恒

B.当A滑到轨道最低点时,轨道对A的支持力大小为2mg

C.下滑过程中重力对A做功的功率一直增大

图2

二、总结

1.轻杆双球模型

轻杆两端(或两处)各固定(刚性固定、铰链连接)一个物体，整个系统一起沿斜面运动、绕某点转动、作一般的平面运动的模型．

2.模型特点

(1)不计杆的质量、大小及运动过程的形变，忽略空气阻力和各种摩擦；

(2)轻杆双球模型平动时两物体线速度相等，绕某点作定轴转动时两物体角速度相等；

(3)轻杆双球模型作一般平面运动时两物体的速度将满足关联关系即两端物体的运动速度按效果进行分解，在沿轻杆方向上二物体的分速度必相等；

(4)杆对物体的作用力不总是沿杆的方向；

(5)杆能对各物体做功(正、负)，单个物体机械能不守恒；

(6)对于杆和物体组成的系统，没有重力以外的外力对系统做功，系统的总机械能守恒.

3.轻杆双球模型问题的实例分析与处理

图3

例1 如图3所示在长为L的硬质轻杆中点A处固定质量为3m的小球，在杆端点B处固定一质量为m的小球，杆可绕无摩擦的轴O转动；现使杆从水平位置无初速度释放，求当杆转到竖直位置的过程中轻杆对A、B两球分别做了多少功？

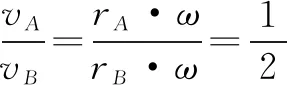
点评(1)本类题目易误认为两球的线速度相等，还易误认为单个小球的机械能守恒.

(2)杆对球的作用力方向不再沿着杆，杆对小球B做正功从而使它的机械能增加，同时杆对小球A做负功，使小球A的机械能减少，系统的机械能守恒.

例2(2015·江苏·14)一转动装置如图4(1)所示,四根轻杆OA、OC、AB和CB与两小球以及一小环通过铰链连接，轻杆长均为L，球和环的质量均为m；轻杆O端固定在竖直的轻质转轴上，套在转轴上的轻质弹簧连接在O与小环之间，轻弹簧原长为L，装置静止时弹簧长为3L/2；转动该装置并缓慢增大转速，小环缓慢上升；弹簧始终在弹性限度内，忽略一切摩擦和空气阻力，重力加速度为g，求 (1)弹簧的劲度系数k；(2)AB杆中弹力为零时，装置转动的角速度ω0；(3)弹簧长度从3L/2缓慢缩短为L/2的过程中，外界对转动装置所做的功W.

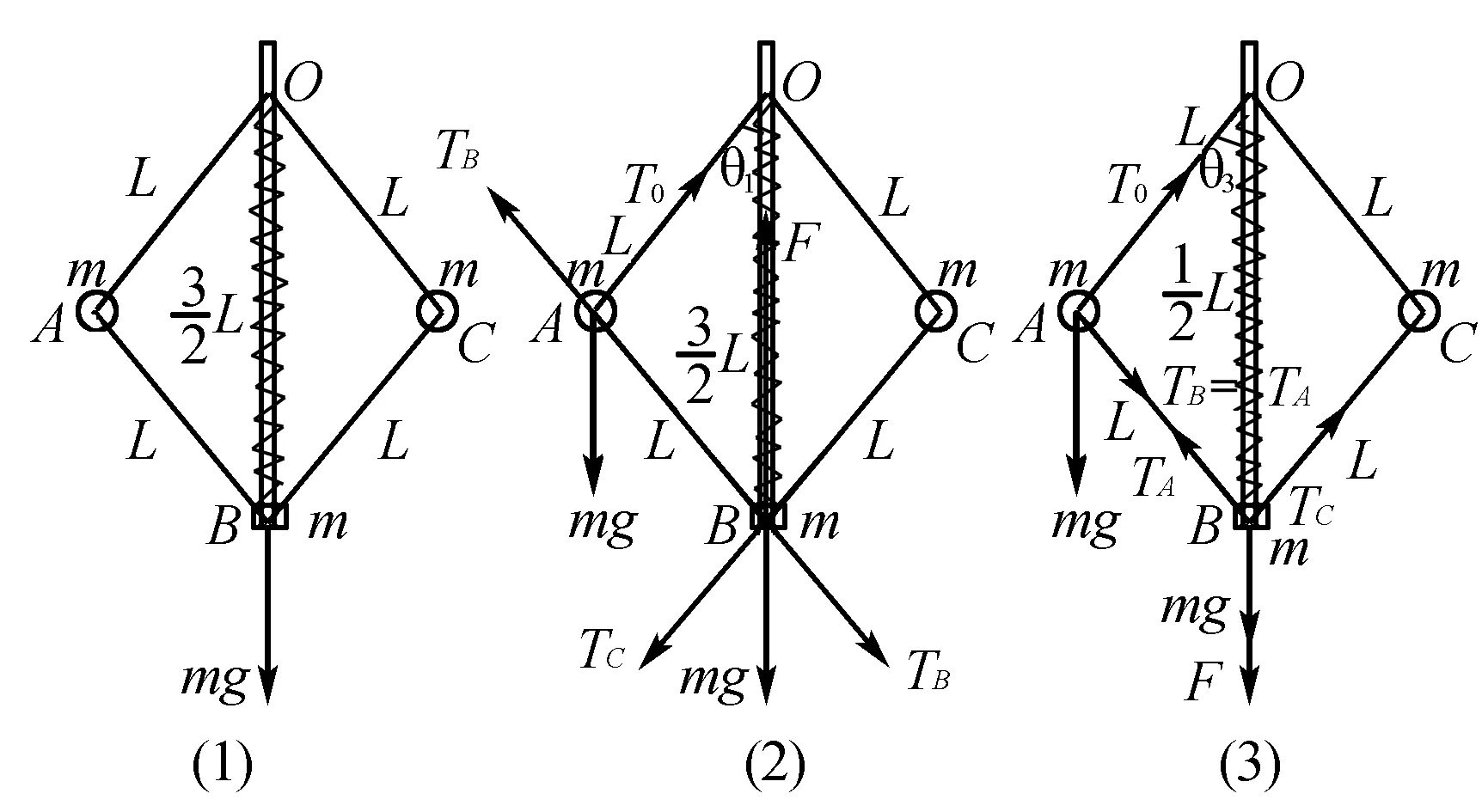
图4

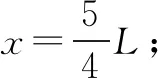
点评由铰链连接的二小球，轻杆上的力必沿轻杆方向；处理时必须能准确的对小环、小球进行受力、状态及运动过程的分析，利用物体的平衡、牛顿第二定律、动能定理求解功和能；要明白不同状态下的几何关系与对应角度的三角函数值的求出；还须注意过程中弹力虽在不断变化，但由于初、末状态形变相等，弹性势能相等，故此过程弹力做功必为0.

例3 (多选)(2015·全国卷Ⅱ 21题)如图4所示滑块a、b的质量均为m，a套在固定竖直杆上，与光滑水平地面相距h，b放在地面上．a、b通过铰链用刚性轻杆连接，由静止释放系统并开始运动．不计摩擦，a、b可视为质点，重力加速度大小为g.则( ).

A．a落地前轻杆对b一直做正功

C．a下落过程中其加速度大小始终不大于g

D．a落地前当a的机械能最小时，b对地面的压力大小为mg

图5

图6

点评(1)刚性轻杆不伸缩，两滑块沿杆的分速度相同．(2)由于杆与物体是通过铰链连接故轻杆对物体的作用力必沿杆的方向，轻杆对滑块a、b都做功，系统机械能守恒．

图7

例4 (2017江苏高考，9，4分)(多选)如图7所示三个小球A、B、C的质量均为m，A与B、C间通过铰链用轻杆连接，轻杆长为L；B、C置于水平地面上，用一轻质弹簧连接，弹簧处于原长；现A由静止释放下降到最低点，两轻杆间夹角α由60°变为120°；A、B、C在同一竖直平面内运动，弹簧在弹性限度内，忽略一切摩擦，重力加速度为g；则此下降过程中( ).

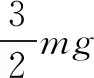
C.弹簧的弹性势能最大时,A的加速度方向竖直向下

点评本题涉及牛顿第二定律、机械能守恒定律等内容.特别是对多物体系统机械能守恒问题,要善于应用机械能转移表达式ΔE重力势能的减小=ΔE弹性势能的增加来分析问题.

4.处理轻杆双球模型实际问题中的注意

(1)明确轻杆双球模型的类型，从而确定两物体的线速度、角速度是否相等，并确定二物体线速度的数量关系；注意二物体通过轻杆相关联时物体速度按效果的分解，抓住沿杆方向二物体的速度相等的关联关系；

(2)杆对物体作用力方向不一定沿着杆，分清是刚性固定或铰链连接；

(3)杆对一个物体做正功，使其机械能增加，同时杆对另一物体做负功，使其机械能减少，故单个物体的机械能不守恒，但系统的机械能守恒.