从Nesbitt不等式引出的探究

安振平

(陕西省咸阳师范学院基础教育课程研究中心 712000)

众所周知，著名Nesbitt不等式(1903)是指：

引题设x,y,z是正实数，求证：

①

不等式①也曾是1963年莫斯科数学竞赛试题，它的证明有20多种.本文探究Nesbitt不等式 ① 的一些变式，由此引发四个方面的有趣的思考，据此证明了一些常见的竞赛不等式.

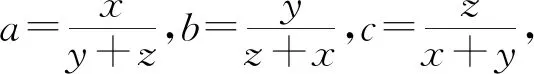
则有

所以

即

ab+bc+ca+2abc=1.

在这里，我们获得：

结论1关系式ab+bc+ca+2abc=1,可以变形为

等价于

依据上文，易知不等式①等价于：

例1设正实数a,b,c满足ab+bc+ca+2abc=1,求证：

②

证明由条件ab+bc+ca+2abc=1,有

应用柯西不等式，得

即

说明若令x=2a,y=2b,z=2c,由不等式②易得2014年罗马尼亚奥林匹克试题：

设正实数x,y,z满足xy+yz+zx+xyz=4,求证：x+y+z≥3.

例2设正实数a,b,c满足ab+bc+ca+2abc=1,求证：

③

证明对条件ab+bc+ca+2abc=1变形，有

应用柯西不等式，得

有

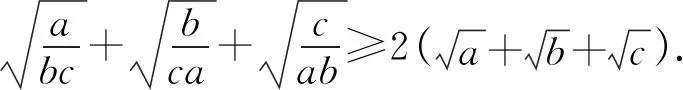
例3设正实数a,b,c满足ab+bc+ca+2abc=1,求证：

a+b+c≥2(ab+bc+ca).

④

证明由条件ab+bc+ca+2abc=1,有

应用柯西不等式，得

即

(a+b+c)+(a2+b2+c2)≥(a+b+c)2,

有

a+b+c≥2(ab+bc+ca).

说明若令x=2a,y=2b,z=2c,由不等式 ④易得1996年越南数学奥林匹克试题：

设正实数x,y,z满足xy+yz+zx+xyz=4,求证：x+y+z≥xy+yz+zx..

在这里，可以获得：

结论2关系式ab+bc+ca+abc=4,可以变形为

等价于

例4设正实数a,b,c满足ab+bc+ca+abc=4,求证：

⑤

证明由条件ab+bc+ca+abc=4,有

应用柯西不等式，得

即

故

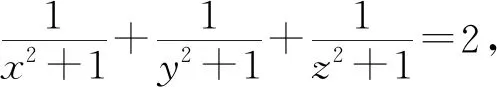
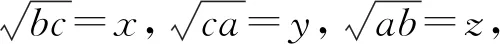
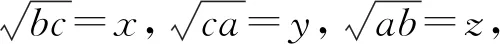
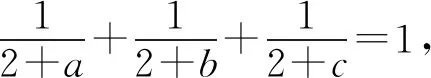
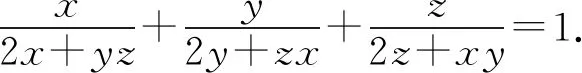
于是，我们获得：

结论3关系式a2+b2+c2+abc=4,可以变形为

等价于

例5设a,b,c是非负实数，且a2+b2+c2+abc=4,求证：

0≤ab+bc+ca-abc≤2.

⑥

证明一方面，由条件a2+b2+c2+abc=4,a,b,c≥0,知a=min{a,b,c}≤1,有

ab+bc+ca-abc≥bc-abc=bc(1-a)≥0,

即

ab+bc+ca-abc≥0.

另一面，由a2+b2+c2+abc=4,有

于是，应用柯西不等式，得

即

2(a2+b2+c2)+3abc≥(a+b+c)2,

得

a2+b2+c2+3abc≥2(ab+bc+ca).

即

4+2abc≥2(ab+bc+ca),

所以

ab+bc+ca-abc≤2.

故

0≤ab+bc+ca-abc≤2.

说明本题是第30届美国数学奥林匹克试题，这里的证明是比较独特和简捷的.

例6设a,b,c是正实数，且a2+b2+c2+abc=4,求证：

a2+b2+c2≥3abc.

⑦

证明由a2+b2+c2+abc=4,有

于是，应用柯西不等式，得

即

2(a2+b2+c2)+3abc≥9abc,

有

a2+b2+c2≥3abc.

例7设a,b,c是正实数，且a2+b2+c2+abc=4,求证：

⑧

证明由a2+b2+c2+abc=4,有

于是，应用柯西不等式，得

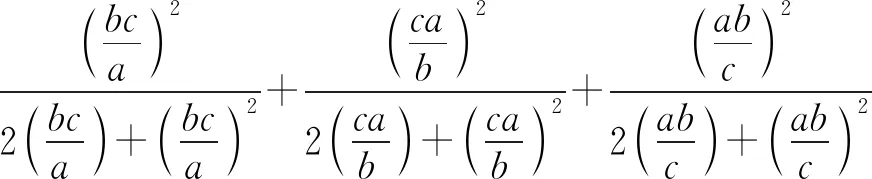
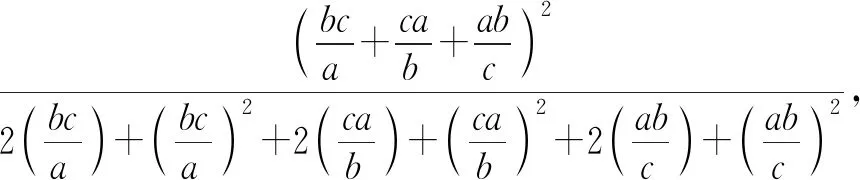
所以

将结论1的关系式ab+bc+ca+2abc=1变形为

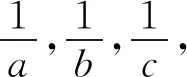
结论4关系式a+b+c+2=abc,可以变形为

等价于

例8设a,b,c是正实数，且a+b+c+2=abc,求证：

⑨

证明由a+b+c+2=abc,可以变形为

应用柯西不等式，得

即

有

所以

例9设a,b,c是正实数，且a+b+c+2=abc,求证：

⑩

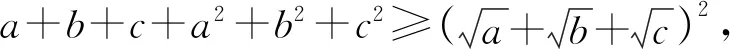
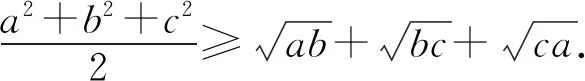
从上文我们不难看出，把整式型的关系式改写为分式型的关系式，想办法应用柯西不等式，证明了一批竞赛题，也导出了一些新颖的不等式.