高三年级学生逻辑推理能力与数学学业成绩的关系研究
端木彦 孔德鹏 黄智华
(南京航空航天大学附属高级中学 210007)
1 问题的提出
推理,是思维的基本形式之一,是由一个或几个已知的判断(前提)推出新判断(结论)的过程.逻辑推理,分为演绎推理与合情推理两类,合情推理又包括类比和归纳.所谓演绎推理,就是从一般性的前提出发,通过推导即“演绎”,得出具体陈述或个别结论的过程,突出从一般到特殊的推理.关于演绎推理,还存在以下几种定义[1]:①演绎推理是从一般到特殊的推理;②它是前提蕴涵结论的推理;③它是前提和结论之间具有必然联系的推理.④演绎推理就是前提与结论之间具有充分条件或充分必要条件联系的必然性推理.所谓合情推理,就是一种比较自然的、合乎情理的,似乎为真的推理,它是根据已有的数学事实和正确的数学结论,或以个人数学经验(数学实验或实践)和数学直观进行推测而得到某些结果的一种推理,常表现为凭直观和联想、直观或直觉等非逻辑思维形式,通过观察、实验、归纳、类比,特殊和一般等方法直接获得某种数学结论[2].
《普通高中数学课程标准(2017版)》把逻辑推理定为6大数学核心素养之一,足见其重要性.对学生数学推理能力的研究,课题组黄智华、渠东剑老师将其总结为以下三类:对比分析研究;对数学推理的认知、心理研究;推理能力及其培养的研究[3].他们以南京市6所高中为调研对象,获得了一些结论:①高中学生的逻辑推理处于中等水平,高中学生的类比推理水平处于低级状态;②逻辑推理在不同年级间无显著性差异,而假言推理、归纳推理和类比推理存在显著性差异;③高一与高二、高一与高三假言推理能力存在有显著性差异,高二与高三假言推理能力无显著性差异;类比推理能力在三个年级之间都有显著性差异;归纳能力在三个年级之间无显著差异;④男生的逻辑推理及其各维度测验的平均分均比女生高,且在逻辑推理上男女之间存在着显著差异.男女生在演绎推理上没有显著差异;在假言推理,命题演算和类比推理上,男女生都存在显著差异[3].
关于逻辑推理能力与学业成绩之间是否存在联系,通过查阅相关文献发现已有一些研究成果.田中等对4~7岁儿童研究的结论是,推理能力的认知成绩的快速提升期是7岁—7岁5个月(初入学)[4].张军翎得出不同学业成绩中小学生的逻辑推理能力存在不平衡性差异:与优秀生相比,中等生的逻辑推理能力明显落后;与中等生相比,困难生的逻辑推理能力显著偏低;逻辑推理能力对学业成绩具有较高的预测性[5].张潮对中小学五个年级的674名学生的研究得出:小学四年级是逻辑推理能力发展的一个值得关注的非常时期,不同学业成绩(优中差)的中小学生逻辑推理能力存在显著差异,逻辑推理能力与数学成绩相关显著,对中小学生的学业成绩具有较高的预测性[6].曾超的结论是:①高二理科生的数学推理能力好于高二文科生;②高二男生的数学推理能力整体上优于高二女生;③高二学生的合情推理能力强于演绎推理能力;④高二学生在平面几何、解析几何、空间几何三大问题的推理能力上表现较弱[7].郭俊楠的结论是:①高三年级的学生数学推理发展水平存在差异性,理科生比文科生强,男生比女生强;②合情推理与演绎推理能力发展不均衡,合情推理能力明显比演绎推理能力要强;③高三年级学生对于合情推理和演绎推理的区分能力欠缺[8].
从研究对象上来看,现有的研究大都分布于幼儿园、小学、初中和高中各个年级,能够较好地反映学生推理能力变化的规律性、发展性和整体性.但是,研究的不足是研究对象年龄跨度较大,并且有的结论过于久远(距今有10年以上),研究缺乏集中性、适时性和时代性.既然逻辑推理是核心素养,那么当下高中三年级(准高考生)的逻辑推理能力如何,与数学学业水平的关系怎样?本研究正是本着这样的初衷,以逻辑推理能力与高三学生的数学学业成绩的相关性为目标进行研究,从而为培养逻辑推理能力促进考生数学学业成绩进步提供实证依据.
2 研究方法
2.1 对推理能力水平的分析
我们研究了国内外已有的推理能力测试问卷、公务员考试真题等,结合课本内容编制试题.为了保证调查结果的科学性和客观性,我们尽可能回避与高考内容直接相关的选题.同时,因临近高考,为免过多占用学生时间,我们调整了题量和难度,最终测试10道题,包括6道选择题、3道填空题和1道解答题.其中类比推理2题、归纳推理4题、演绎推理4题.作为分值最高的一道测试演绎推理能力的解答题,兼含分类讨论、数形结合等数学思想方法的考查,故答案形式不限,按作答要素得分.
数据采用SPSS15.0 for windows进行处理和分析,先对调查问卷作了信度检验,对测试数据的同质性信度进行分析,内部一致性系数即α系数为0.576,表明测试卷具有较高的信度.然后采用相关分析、回归分析和独立样本T检验对高三年级学生逻辑推理能力和数学学业成绩进行分析和检验.
2.2 抽样测试与访谈
在2018年5月对南京市区某四星级高中高三年级学生进行了测试,总体样本157人.
为了保证测试的有效性,我们规定了“用时相同”、“独立完成”、“注明性别、文理选科”的测试要求.同时选取被试者在高三学年内参加的南京市四次统考成绩的平均值作为对应的学业成绩.
测试结束后,随机抽取若干名被试,由测试人进行个别访谈,并记录学生作答时的思路和想法.
3 测试统计与抽样访谈结果
3.1 高三年级逻辑推理能力与数学学业成绩的相关分析
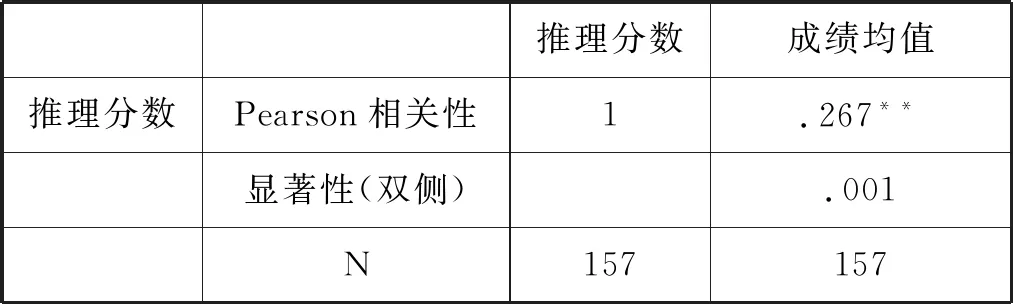
表1 逻辑推理能力与数学成绩的相关性
**.在.01 水平(双侧)上显著相关
由表1可以看出:高三学生的推理分数与学习成绩之间的相关系数是0.267,相关系数大于0.05,且在0.01水平上呈显著相关.说明高三学生的逻辑推理与学业成绩之间有着密切的关系.
3.2 高三年级逻辑推理能力与数学学业成绩的回归分析
以高三学生的推理成绩作为自变量,各阶段数学成绩的均值作为因变量作回归分析,结果如表2:
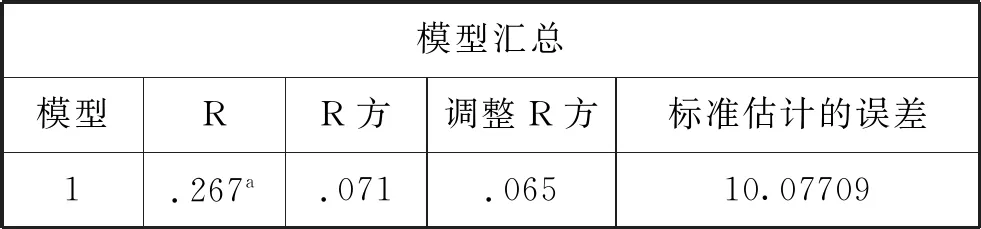
表2 推理能力与数学成绩的回归分析
a.预测变量: (常量), 推理分数

Anovab
a.预测变量: (常量), 推理分数
b.因变量: 成绩均值

系数a
a.因变量: 成绩均值
由表2可以看出:
(1)在“模型汇总”中,R是推理成绩与成绩均值的相关系数,R方是因变量均分的变异中被回归方程解释的比例,即高三学生的数学成绩有7.1%是由推理能力引起的.
(2)在“方差分析表检验模型”中,p=0.001<0.05,表明回归显著,回归方程具有良好的代表性.
(3)“回归系数及检验表”反映了回归系数和各系数的显著性检验,p=0.000,p=0.001,表明推理能力对学生数学成绩的影响显著.
回归模型的方程为:y=91.379+0.285x.
这个结果表明,高三学生的逻辑推理水平对数学学业成绩有预测作用,逻辑推理能力对学业成绩有直接的影响作用.
3.3 文理科逻辑推理能力的独立样本T检验
观察表3“方差方程的Levene检验”中,Sig=0.679>0.05,表示方差没有差异,即方差相等,此时选择假设方差相等一行的数据作为检验结果,即观察“均值方程的t检验”Sig的值,而此时Sig=0.131>0.05,这表示文科和理科的学生在逻辑推理能力上没有显著性差异.
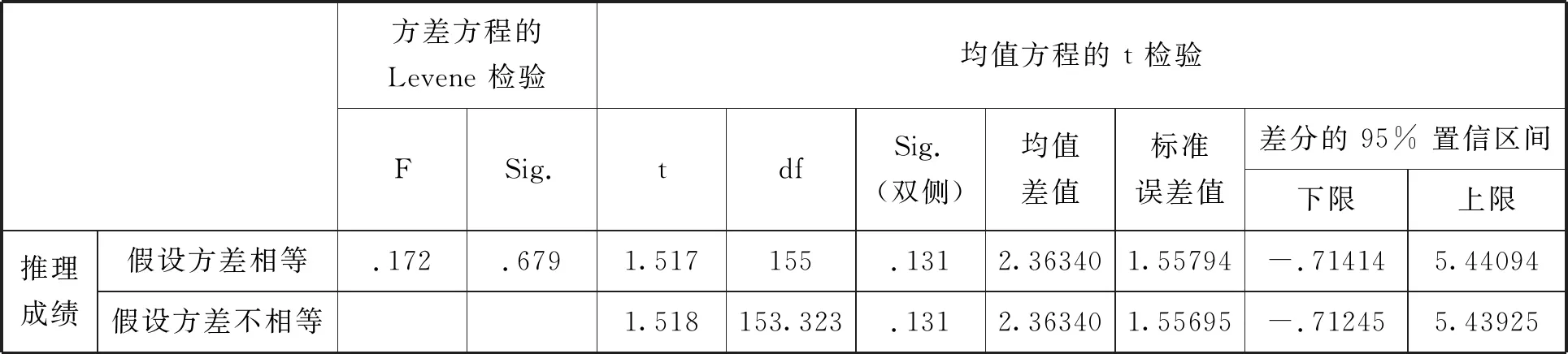
表3 文理科逻辑推理能力的独立样本检验
3.4 男女生的独立样本T检验
由表4可以看出,“方差方程的Levene检验”中,Sig=0.741>0.05,表示方差没有差异,即方差相等,此时选择假设方差相等一行的数据作为检验结果,即观察“均值方程的t 检验”Sig的值,而此时Sig=0.000<0.05,这表示男生和女生在逻辑推理能力上存在显著差异.
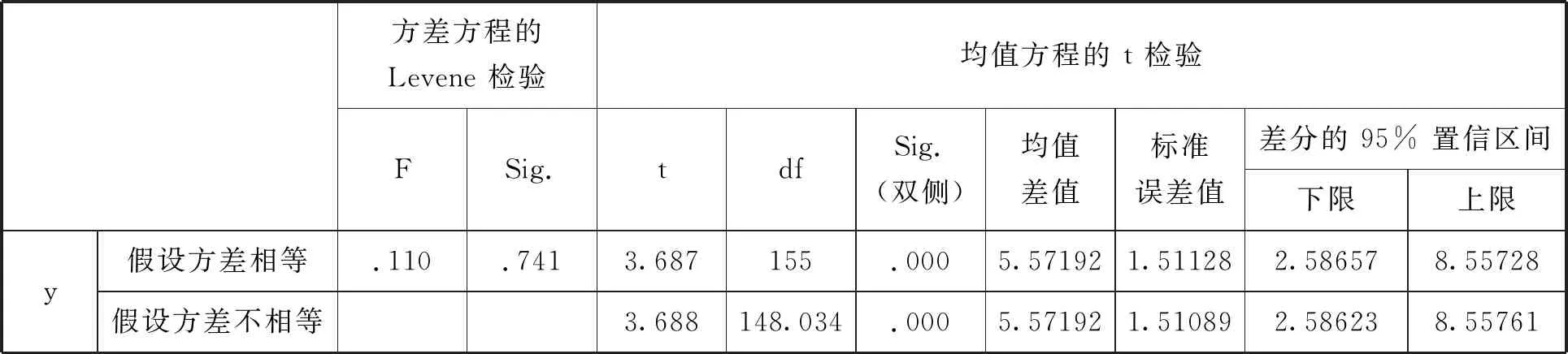
表4 男女生的独立样本检验
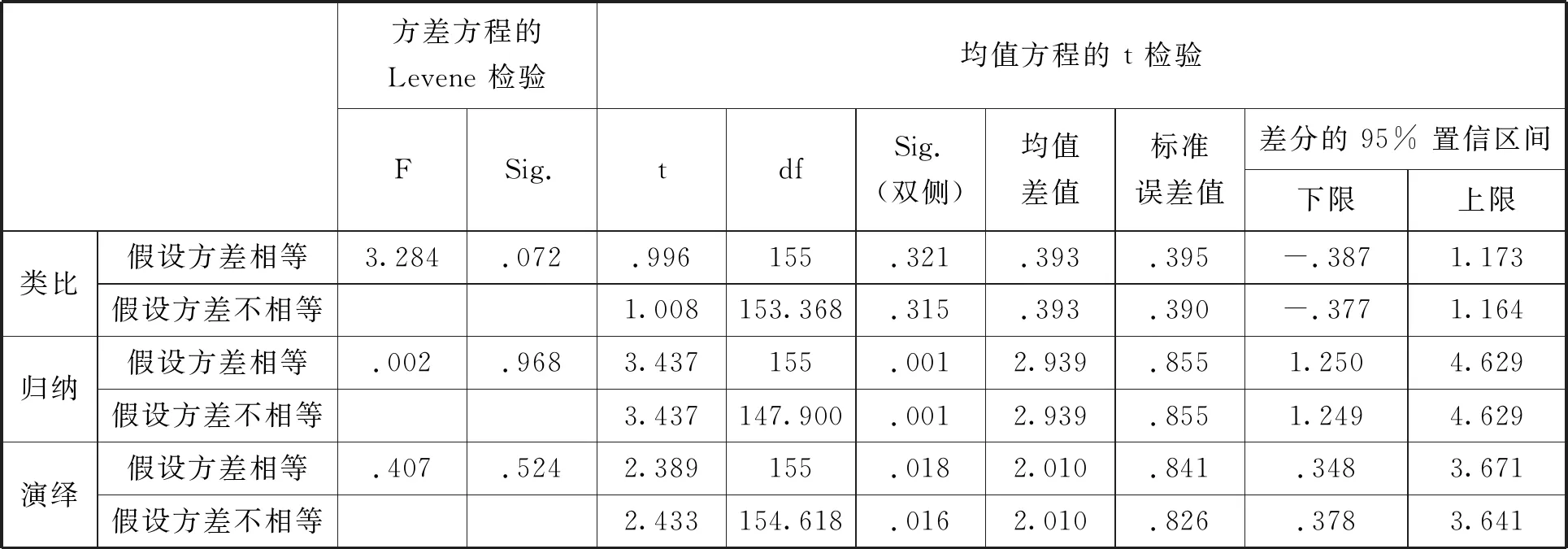
表5 男女生在三个维度上的独立样本t检验
3.5 高三年级推理高分组和推理低分组的数学学习成绩独立样本T检验
计算高三年级推理成绩的均值和标准差,得到均值为31.8981,标准差为9.78499.按照学生的推理得分分组,高于均分加标准差的为高分组(A组),低于均分减标准差的为低分组(B组),然后将两组的数学学习成绩作T检验,得到下面表6.
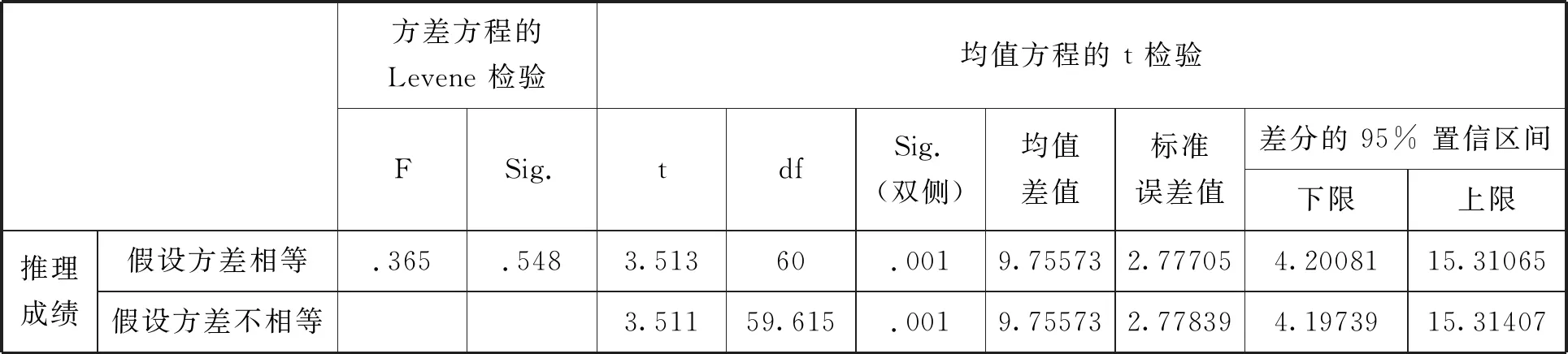
表6 高分组和低分组成绩独立样本检验
观察“方差方程的Levene检验”中,Sig=0.548>0.05,表示方差没有差异,即方差相等,此时选择假设方差相等一行的数据作为检验结果,即观察“均值方程的t 检验”Sig的值,而此时Sig=0.001<0.01,这表示高分组和低分组的学生在数学学习成绩上有显著性差异.
3.6 抽样访谈结果
共抽取高分组10人和低分组10人(其中文科9人,理科11人,男生12人,女生8人),进行个别访谈,逐题请学生说明作答理由.
高分组都表现出典型的逻辑推理水平,错误归因中“粗心”出现占比较高.比如在回答20183的“分裂”中最大的数时,高分组绝大多数都已得出20182+2017的正确答案,但在继续计算其最简结果时产生错误.相对地,低分组的作答理由多为“列举、数出”或是“猜的”,错误归因中,认为自己“概念模糊”的人数较多.例如,“等差数列”中的“和运算”应该与“等比数列”中的何种运算进行运算结构类比?齿轮的“逆时针”旋转究竟是哪个方向?“复数”与“负数”究竟是什么关系?等等.
也有一些错误比较特别.
学生A(低分组,文科,女生)
问:22018的个位数字为什么选择了6?(考查归纳推理,正确答案是4)
答:我记得28的个位数字是6.
问:为什么认为22018与28的个位数字是一样的?(应由周期性发现其个位数字与22一致)
答:我用了类比推理.
可见,样本对推理是有些感受的,但是拘于表面相似性识别联想,未进行实质分析.她认为自己运用了类比推理,殊不知实际还是归纳推理,只不过缺少了特殊到一般的归纳过程,而是凭感觉猜想周期.猜想是尚未辨明真假的数学叙述,它的正确与否需要演绎推理加以证明,而这恰是高分组与低分组被试在解题思路和科学精神上的一个明显差异.
学生B(高分组,理科,女生)
问:为什么在完成第10题时,将原先的分类想法都杠去了?(题为“过一点作一条直线,如何平分平面内的三角形?”)
答:我当时觉得点的位置不确定,就先把所有可能性都写出来了.
问:你原本分了点为顶点、点在边上、点在形内、点在形外四种情况.
答:对,但是我在解决“点在形内”时,发现还要二次分类讨论,觉得不对了.
本题是基于分类讨论思想的演绎推理题.其实无论点在形内、形上、形外,本质只分为两大类:若点在某边中线所在直线上,则该直线即为所求;若点不在任意一边中线所在直线上,则应根据面积公式作出满足相应线段比例关系的直线.在高中数学学习中,演绎推理更多的表现为学生在解决问题时的一种思考方法,随着演绎推理能力的提升,学生能够更加熟练地进行透视本质的科学思维,或是创造性地解决问题.可以说演绎推理是学生进行深度思考时的心理学基础.
学生C(高分组,理科,男生)
问:保持长方体容器的一边固定于地面上,再将容器倾斜,为什么你认为水面四边形的面积不改变?
答:我当时把矿泉水瓶子摆了一下,觉得水面椭圆的面积就是固定的.
问:只是形状保持为椭圆吧,一旦改变倾斜角度,面积也会改变.
答:啊?我没看到这个条件.(题中有条件“随着倾斜度的不同”)
样本在解决问题时已经自觉使用了由抽象到具体的分析方法,表面看来,犯的是“粗心”的错误,与推理能力无关.但是对题中反复出现的“随着”、“当”、“始终”、“定值”等等词语的加工转化能力缺失,可能影响到推理能力的测评结果,也可以认为这表现出某种语义形式方面推理能力的欠缺.
从访谈结果看,所有对象均具备一定的推理能力,其中男生归纳推理能力较强于女生,类比推理能力无明显差异.演绎推理能力在文理科无明显差异,但男生略高于女生.演绎推理在高分组和低分组差异最为明显,与学业成绩相关度较高.
4 分析与讨论
4.1 合情推理能力
通过进一步对男女生在三个维度上进行独立样本t检验(表5),我们发现,归纳维度在0.01水平存在显著差异,说明高三学生中男生较女生更擅于运用归纳推理处理问题.归纳推理与被试的知识经验有着密切的关系.已有的许多研究表明:当人们缺乏归纳推理任务中所需要的知识时,通常会根据客体、事件等之间的相似性来进行归纳推理;一旦人们获得了相关的知识,知识在归纳推理中的作用就会凸显出来.研究提示:教学中教师可以适当对女生作针对性引导,帮助女生形成归纳推理思维习惯,提升推理能力.
分析显示:高三学生类比推理能力不存在性别显著差异.结合访谈发现,文理科差异也不具有显著性意义.同时,访谈中也发现,低分组被试受限于信息贮存量及信息加工技术,习惯于语词联想法获取结果.高分组被试受益于认知策略,可以推断出因果、并列关系,整体/部分、包含关系,类比对象间相互作用维度等要素后获取正确结果.
高中数学教材中的定理,往往通过合情推理引出,再由演绎推理进行论证.相较于初中教材设计,更符合学生的认知特点,也符合从特殊到一般的认知规律.“探索是数学教学的生命线”,在问题解决的教学中,教师也不妨多借由归纳推理和类比推理探索解决问题的思路和方向,继而借助演绎推理论证猜想.
结合以上分析,对于合情推理教学提出如下思考.教学中适度鼓励学生采用通过合情推理获得初步结果后再行证明的思维方式.指导学生通过与条件或结论相似的题型进行形式与实质的类比,进行解题思路的迁移.同时教师应关注学生进行合情推理的宽度和精准度.
4.2 演绎推理能力
我国学者李丹、方富熹和胡竹菁等人和国外学者伍德沃斯、斯滕伯格和德索托等人对演绎推理做出的研究发现,经过几次飞跃,演绎推理能力在高中阶段已经趋于成熟.演绎推理能力不仅与推理形式和规则有关,也与学生的知识程度密切相关.
表5显示,男女生演绎维度在0.05水平有显著差异.通过访谈,我们还发现,高分组与低分组在演绎推理能力上的差异主要表现在:1.对材料迅速而准确的抽象概况能力;2.用简捷的结构进行思维的能力;3.在逻辑推理过程中的自省能力.
以上分析为演绎推理教学提供了一些启示.加强数学活动过程教学,注重学生思维过程中的暂停和后续,引导学生关注每个逻辑段的逻辑联系,有意识的进行相关联想.在材料的选择上,要将符号语言与文字、图形材料等表现形式结合起来进行推理训练.
5 结论
本次研究得到以下结论:
(1)高三年级学生逻辑推理能力与数学学业成绩之间存在密切联系;逻辑推理水平对数学学业成绩有预测作用,逻辑推理能力对学业成绩有直接的影响作用.
(2)文科和理科的学生在逻辑推理能力上不存在显著性差异;男生和女生在逻辑推理能力上存在显著性差异.
(3)逻辑推理能力的高分组和低分组的学生在数学学习成绩上存在显著性差异.
(致谢:本研究在喻平教授团队的支持下完成,特别感谢韩钰颖和倪霞美两位研究生在数据处理方面所做的工作)

