把握本质 精心设计

王弟成

(连云港市教育局教研室 222006)

1 听课中发现问题

2 学生真的不懂

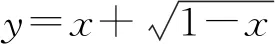
3 教师要理解数学

章建跃博士指出数学教师要教好数学，就要做到“理解数学”、“理解学生”、“理解教学”.“理解数学”是教好数学的前提.“理解数学”即数学教师自己要理解数学问题的本质，知道知识的来龙去脉，乃至于概念形成背后的思想方法.自己不理解谈何教学生理解.只有自己理解了才能谈教学方法问题.课后与任课教师交流，为什么要设2x-2-x=t，这样设为什么就能解决问题？学生设2x=t>0换元后为什么不继续求解下去？老师回答不出所以然.从学生的解答交流反映，不是一个老师不理解这样的问题.当然可能老师每天都教学生解题，一题题解，不是不理解，而是没有去系统思考这些问题.这正是目前教学欠缺的！现在的各级各类培训，过多的是培训教学方法与理念，但对具体数学问题培训过少，他们(包括学校的管理者)可能认为数学老师还能不懂数学.事实是数学老师有很多数学不懂，从全市教师基本功考核看，老师不懂的地方还很多.当然，这也是正常的，这需要数学教师不断学习数学.

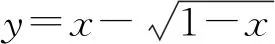
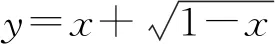
4 对核心内容要精心设计

《普通高中数学课程标准(2017年版)》的课程基本理念第三条是“把握数学本质，启发思考，改进教学”“高中数学教学以启发学生数学学科核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质.”学习数学就要学习数学的本质.数学的本质要通过教师的精心“创设合适的教学情境”，设计精致的教学过程，“启发学生思考”，从而把握问题的本质.对核心概念、思想、方法教师要精心设计，从学生最近发展区出发，设计有联系的学习情境，设计思维连贯的问题串，在联系、对比、变化、拓展问题中把握本质，理解本质.这些核心内容正是学生的思维生长点，是学生能力形成的核心点，是学生形成原创思维的好载体，教学切不可一笔带过.

学生理解换元法的本质与用换元法求函数的值域就是重要内容，教学需要专题设计，系统学习，重点教学，让学生理解透彻.笔者在文[1]中对引入换元法设计了如下求解问题.

问题1：求函数f(x)=x2+2x在[0,10]上的最大值和最小值.

其意图是让学生理解换元法解决此类问题不是必须的，知道寻求函数单调性才是解题关键，换元法只是手段之一，如本题用平方法更好.当然以后可以介绍双换元法.

其意图让学生理解换元的方法，换元后结构要有利于知道单调性.同时介绍另一种换元方法，此题利用其内在关系换元，并不是直接对其中一某项换元，真正理解所换的“元”，要能表示其它项，打通结构.且结构要是自己熟悉的.

问题7：求函数f(x)=4x+4-x-2x+2-x+1的最大值和最小值.

其意图是变换情境让学生进一步理解换元的方法，也看学生是否真正理解利用换元法解决问题的本质.后续三角学习还会遇到求函数y=sinx+cosx+sinxcosx的值域，再进一步强化.

这样设计能让学生透彻理解数学的本质，提高学生对方法的理解，提高学生分析问题能力、解决问题能力.能让学生在对比与联系中理解数学，理解解题方法，而不是孤立学习一种方法、技巧.教学需要这样的研究设计，这样的研究设计才是教学.