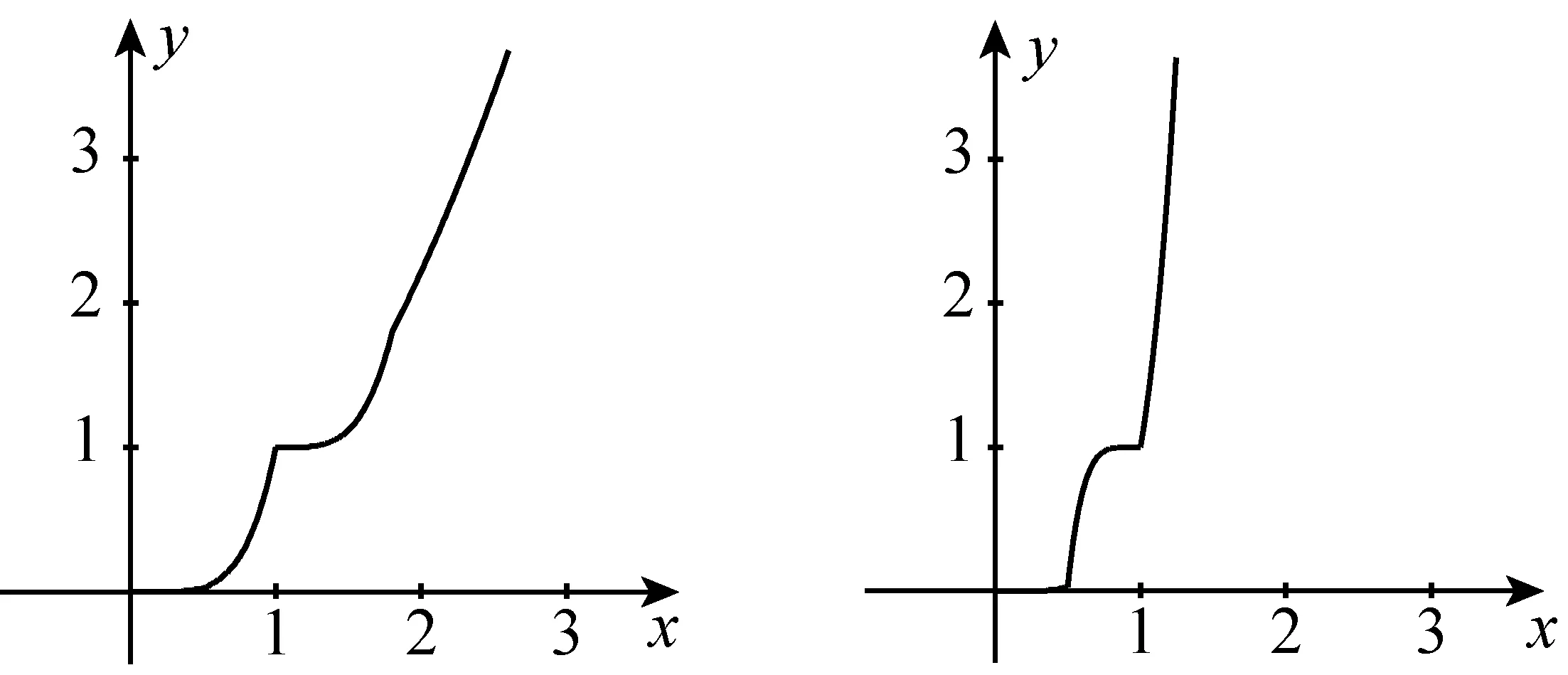
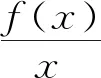关于“L函数”的一则注记
——对一道二模试题的探究
汪 健
(华东师范大学第二附属中学 201203)
题若函数f(x)满足:对于任意正数s、t,都有f(s)>0、f(t)>0,f(s)+f(t) (2)若函数g(x)=3x-1+a(3-x-1)为“L函数”,求实数a的取值范围; 这是2017年上海市黄浦区高三数学二模试卷的最后一题.其第三小题的证明可化归为以下命题. (i)s+t≤1. 由二项式定理即得 fn(s)+fn(t)=sn+tn <(s+t)n=fn(s+t). 令d=s+t-1,则s-d=1-t, 故由y=xn的凸性, fn(s)+fn(t)=sn+tn≤dn+1. 另一方面, 而d∈(0,1),故dn+1<1+dn-1, 从而fn(s)+fn(t) =s+t≥sn+tn=fn(s)+fn(t). 由二项式定理, fn(s+t)-fn(t)= 故fn(s)+fn(t) fn(s)=sn≤s, 而同(iii)可得fn(s+t)>s+t, 故fn(s)+fn(t) 因此fn(s)≤1+(s-1)=s, ≥fn(s)+fn(t). 展开完全平方得 >s≥sn=fn(s), 故fn(s)+fn(t) fn(s)≤1+(s-1)=s 故fn(s)+fn(t) 故fn(x)是“L函数”. 故fn(x0) 命题2已知函数f(x)为“L函数”,且f(1)=1.若f(x)<λx对一切0 证明对任意的0 由二项式定理,显然 gn(s)+gn(t) 由y=xn的凸性, 又(1-2d)n≤1-2d, 故gn(s)+gn(t) 易知, gn(s)+gn(t)=sn+1-(2n-1)(1-t)n, gn(s+t)=1-(2n-1)(1-s-t)n, 于是gn(s+t)-gn(s)-gn(t) =(2n-1)[(1-t)n-(1-s-t)n]-sn. gn(s+t)-gn(s)-gn(t) =(1-t)n[(2n-1)(1-un)-(1-u)n]. 由s+t≤1知t<1,从而u∈(0,1), 故gn(s+t)-gn(s)-gn(t) 显然,当n>2时,上式右端为正, 故gn(s)+gn(t) 考虑函数g(s)=sn-(s+t)n+1, g′(s)=nsn-1-(n+1)(s+t)n gn(s)+gn(t)-gn(s+t) =sn-(s+t)n+1+1-(2n-1)(1-t)n, 也是关于s的减函数. 由此可知, gn(s)+gn(t)-gn(s+t) 即gn(s)+gn(t) 由函数y=1-(2n-1)(1-x)n(x∈[0,1])的凸性知, gn(s+t)=(2u)n+1, 从而gn(s+t)-gn(s)-gn(t) ≥(2u)n+1-2[1-(2n-1)(1-u)n]. ≥2n+1[un+1+(1-u)n+1]-2, 故2n+1[un+1+(1-u)n+1]-2>0, 从而gn(s)+gn(t) gn(s+t)=(s+t)n+1>tn+1+(n+1)tsn >tn+1+sn=gn(t)+gn(s) gn(s+t)=(s+t)n+1>tn+1+(n+1)tns h)s>1. 由二项式定理,显然 gn(s)+gn(t) 故gn(x)是“L函数”. 故δ1/(n+1)>δln(1-δ)/lnδ=1-δ, 或者等价地,δ>1-δ1/(n+1). >2-4ε-2(1-2ε)n+1, 又因为4ε<2δ且(1-2ε)n+1<δ, 从而gn(x0)>kx0. 上述问题可以通过选择适当的单位分解[2],将不连续的“L函数”(如S(x))“磨光”成光滑的来加以解决,具体细节留给读者作为练习. 其次,新概念“L函数”的命名也值得商榷.从定义的核心部分,不等式f(s)+f(t) 不仅如此,前文所举的“L函数”fn(x)与gn(x)的图象所表现出的凸性(如下图所示)说明,“L函数”的图像在局部上的形状更加接近于J形或G形.此外,不连续的“L函数”S(x)的图像也呈现出与上述两族函数类似的“凸”阶梯函数的形象. 不过,“L函数”、“G函数”和“J函数”的名称都在数学中已有特定的意义[3],故此,笔者认为,为“L函数”另择名称似乎更为妥当.
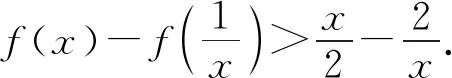

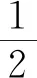
1 最佳下界的验证
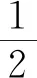
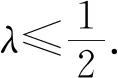
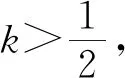
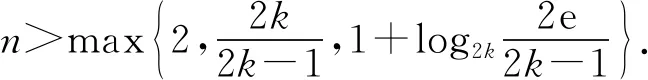
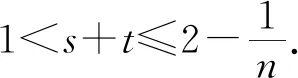
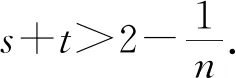
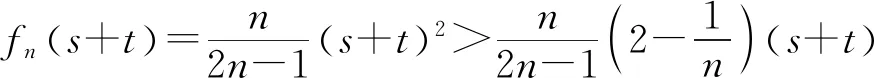
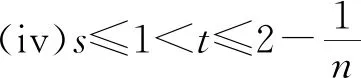
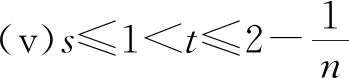
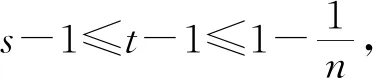
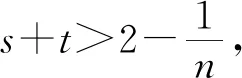
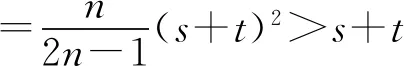

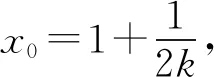
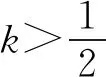
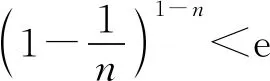
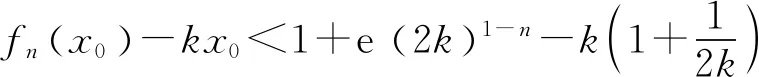
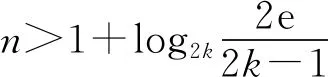

2 最佳上界的验证
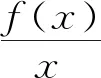
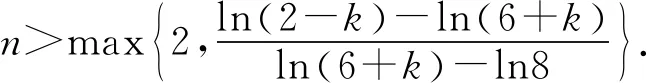
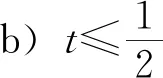
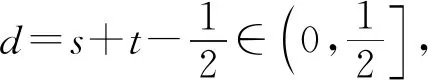
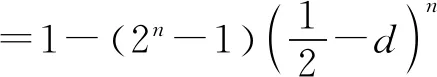
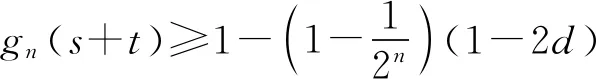
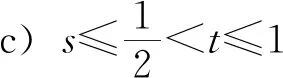
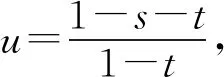

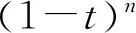

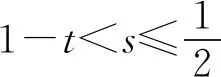
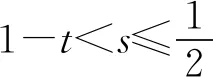
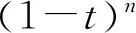
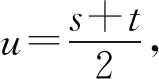
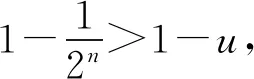
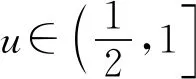
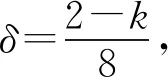
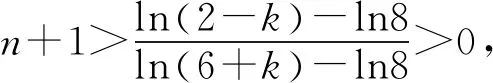
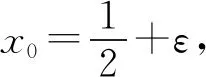
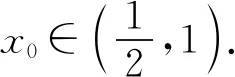
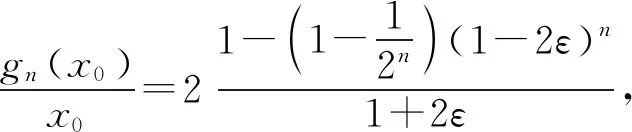
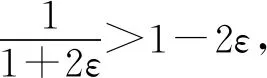
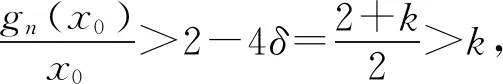
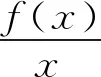
3 进一步的思考