数学问题解答

2019年5月号问题解答

(解答由问题提供人给出)

2481设a,b,c>0,证明：

(安徽省六安第二中学 陶兴红 237005)

证明由均值不等式得

由柯西不等式得

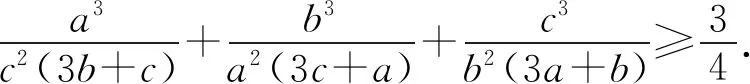
当且仅当a=b=c时取等号.

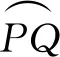
(安徽省枞阳县宏实中学 江保兵 246700 )

证明连接O1A,O1B,O1D,O1O2,O1P,O1Q,PQ，设O1O2与PQ的交点为点F.

由题意O1O2⊥PQ，O1P=O1Q，所以∠O1PF=∠O1QF=∠PBO1，

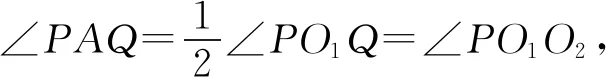
所以 ∠PAQ+∠PBO1=∠PO1F+∠O1PF=90°，

即BO1⊥AC，

在圆O2中，BD为直径，BO1⊥DO1,

所以AC//O1D;

同理CO1⊥AB，

即O1为△ABC的垂心，有AO1⊥BC.

在圆O2中，BD为直径，

所以CD⊥BC,所以AO1//CD;

所以四边形AO1DC为平行四边形，

即CD=AO1=r.

2483在△ABC中，求证：

(四川成都金牛西林巷18号晨曦数学工作室 宿晓阳 610031)

证明先证在△ABC中，有

(1)

事实上，由

易知(1)式等价于

这是三角形中的常用恒等式，显然成立.

故(1)式成立.于是在(1)式中作变换

即知证式成立.

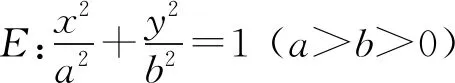
(河南省方城县教研室 邵明宪 473200)

得AB//CD.

故△MBA∽△MDC(不妨如图1)．

图1

设AB、CD的中点分别为F、G，

连结MF、MG．则由△MBA∽△MDC，

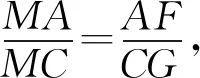
故∠FMA=∠GMC．

同理∠FMB=∠GMD．

于是∠FMB+∠BMC+∠CMG=∠CMD+∠BMC=180°，

从而F、M、G三点共线．

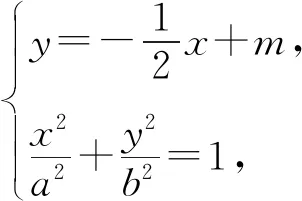
得(a2+4b2)x2-4a2mx+4a2(m2-b2)=0，

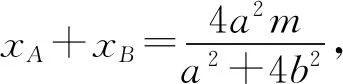
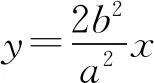
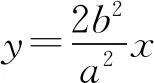
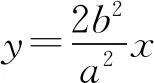
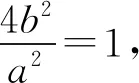
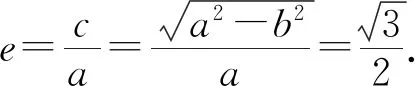
2485在△ABC中,设a,b,c,ha,hb,hc,R分别为三边长、三个高线长及外接圆半径,指数p为正数,求证

(1)

(天津水运高级技工学校 黄兆麟 300456)

证明首先证明一个结论

由不等式(1)的全对称性,不妨设A≥B≥C,则有

同时有1-2cosA≥0及1-2cosC≤0.

又设不等式(1)左右之差为M,并注意到有ha=2RsinBsinC,那么

即原不等式成立.

2019年6月号问题

(来稿请注明出处——编者)

(河南省南阳师范学院软件学院 李居之 孙文雪 473061)

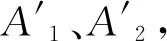
图1

(成都市金牛区蜀汉路369号2-2-35 张殿书 610036)

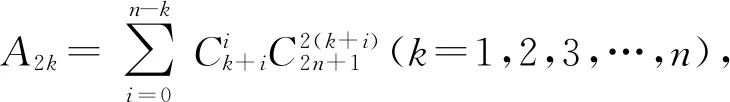
A0x2n+1-A2x2n-1+A4x2n-3-A6x2n-5+…+(-1)nA2nx+(-1)n+1sin(2n+1)α=0

(1)

(河南质量工程职业学院 李永利 467000)

2489已知O为锐角△ABC的外心，过O的直线交AB、AC所在的直线于P、Q两点.求证：

(江西省高安市石脑二中 王典辉 330818)

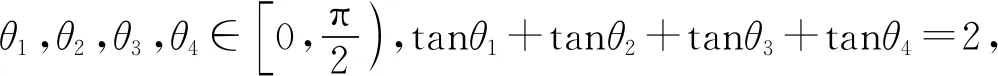
(河南辉县一中 贺基军 453600)