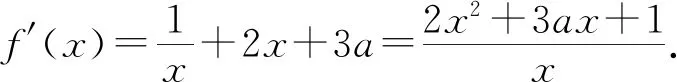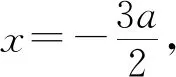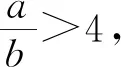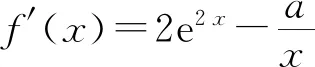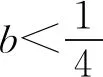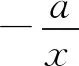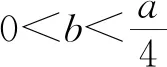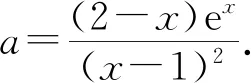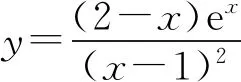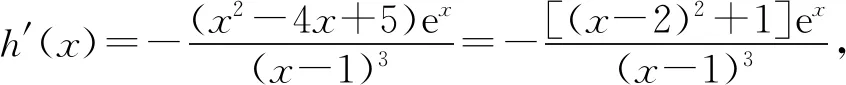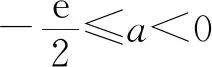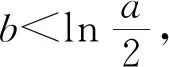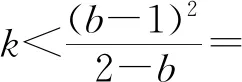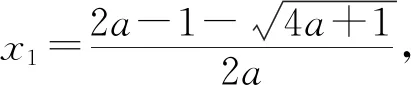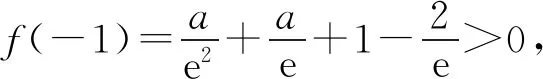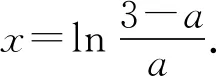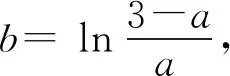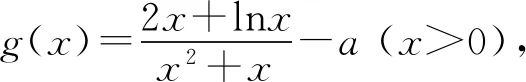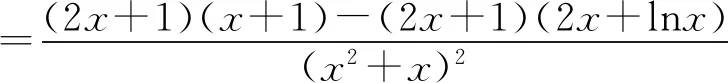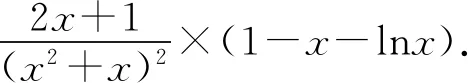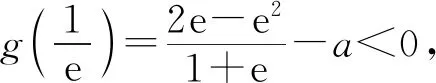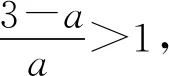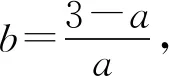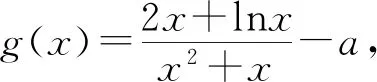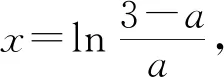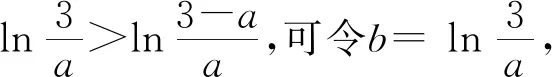函数零点看端详异号连续细思量

2019-08-22 01:00王芝平李亚斌

数学通报 2019年6期

王芝平李亚斌

(1.北京宏志中学 100013；2.黑龙江省农垦总局人社局 150036)

若f(x0)=0，则称x0是函数f(x)的零点.显然函数的零点就是该函数的图象与x轴交点的横坐标.所以函数零点问题也可转化为函数图象与x轴交点问题来处理，甚至转化为两个函数的图象交点来处理.解答这类问题，首先要明确基本初等函数零点问题的解决方法，其次要熟练应用 “函数零点存在性定理”：

如果函数f(x)在区间[a，b]上的图象是连续不断的一条曲线，并且有f(a)f(b)<0，那么，函数f(x)在区间(a，b)内有零点，即存在c∈(a，b)，使得f(c)=0，这个也就是方程f(x)=0的根．[1]

若继续研究函数零点个数问题，则可借助函数的单调性予以讨论：

如果f(x)在区间(a，b)上是单调函数，那么f(x)在区间(a，b)上最多有一个零点.

函数零点问题不但能充分体现函数与方程、分类与整合、数形结合、转化与化归等重要思想方法，而且涉及知识面广，综合性强，对数学素养要求较高.特别地，恰当“取点”使其函数值大于0或小于0是解题顺利进行的一个瓶颈，但许多解法对如何“取点”也不做解释，或语焉不详，让人感觉到像“魔术师帽子里的兔子”般神奇.我们认为，教育部考试中心公布的高考试题的“标准答案”主要是供阅卷参考使用的，不宜机械地照搬到课堂教学中去.本文介绍笔者在解决这类问题时的一些基本想法，供大家教学时参考，并请方家指正.

例1(2019年陕西省第一次质量检测理科第21题)已知函数f(x)=lnx+x2+3ax+1 (a∈R).

(Ⅰ)略； (Ⅱ)当a<-1时，讨论函数f(x)的零点个数.

(1)谋定思路有方向

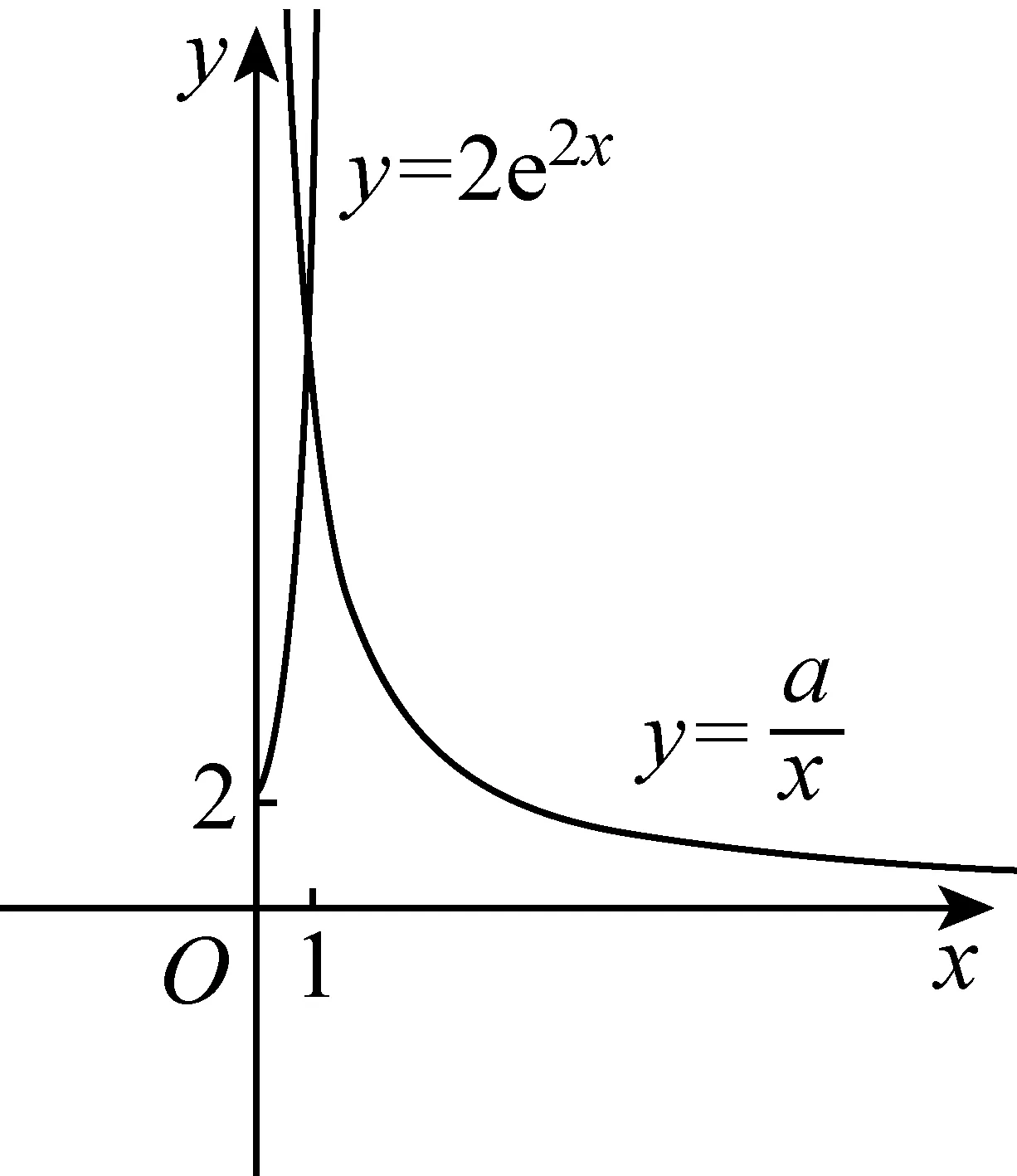
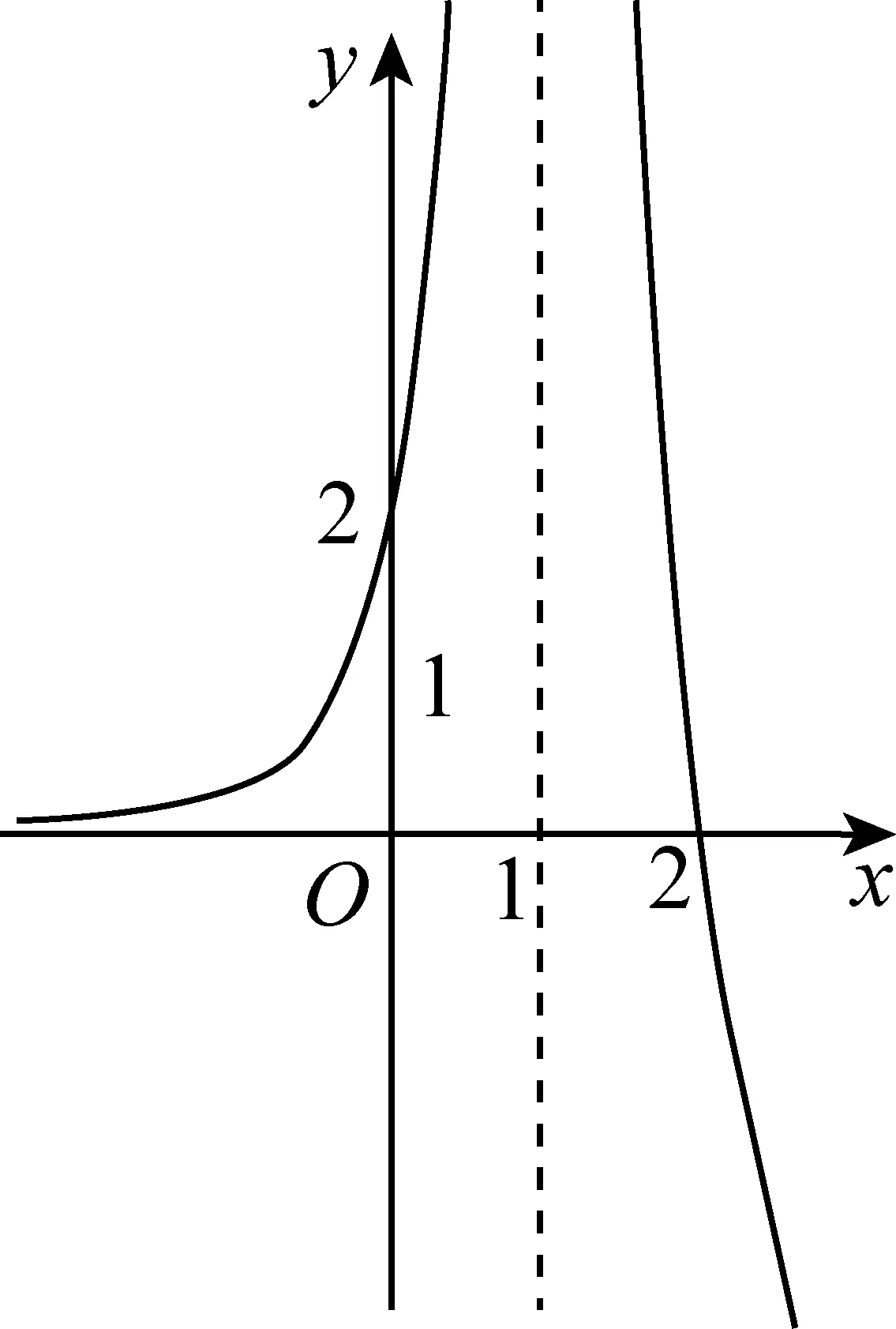
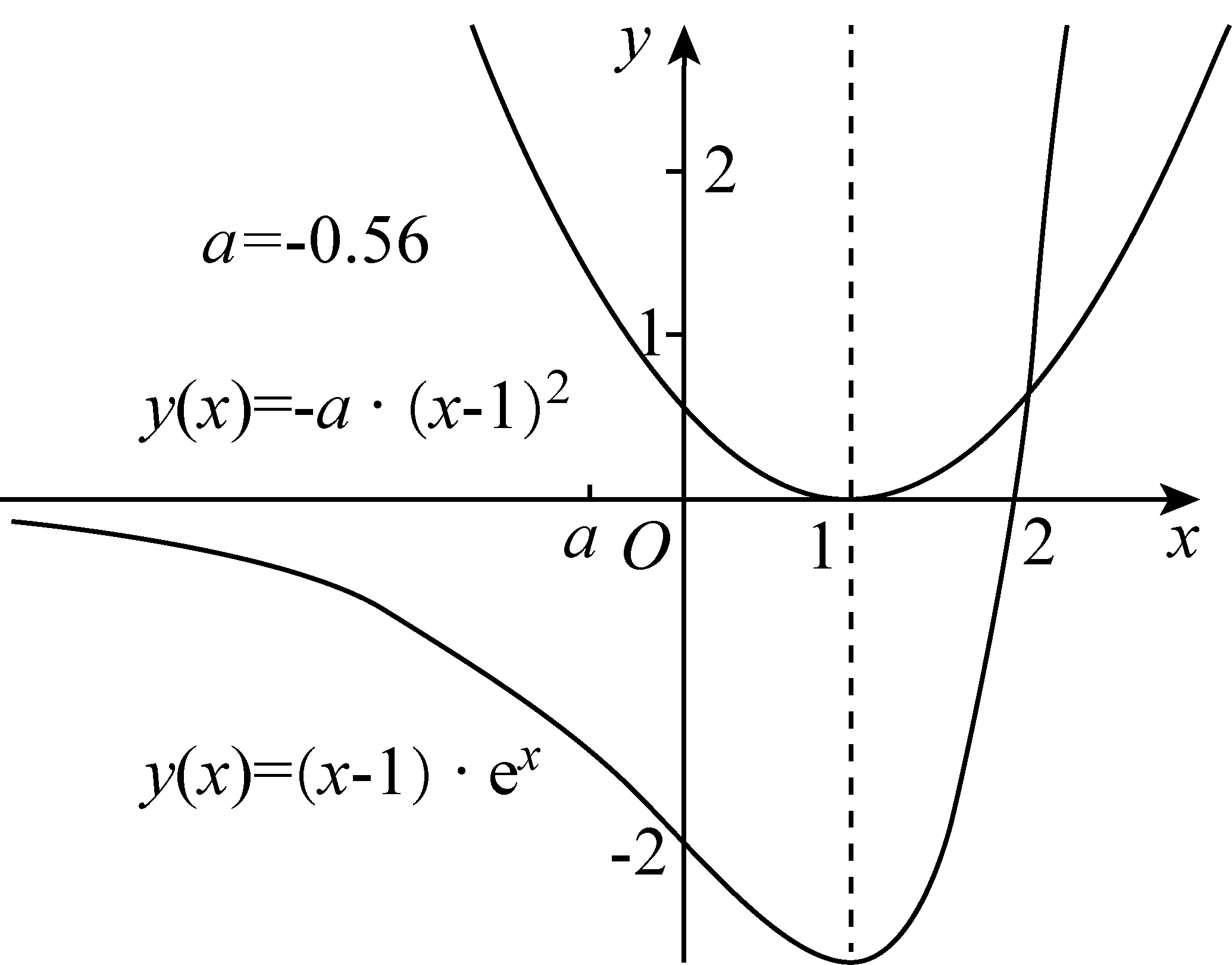
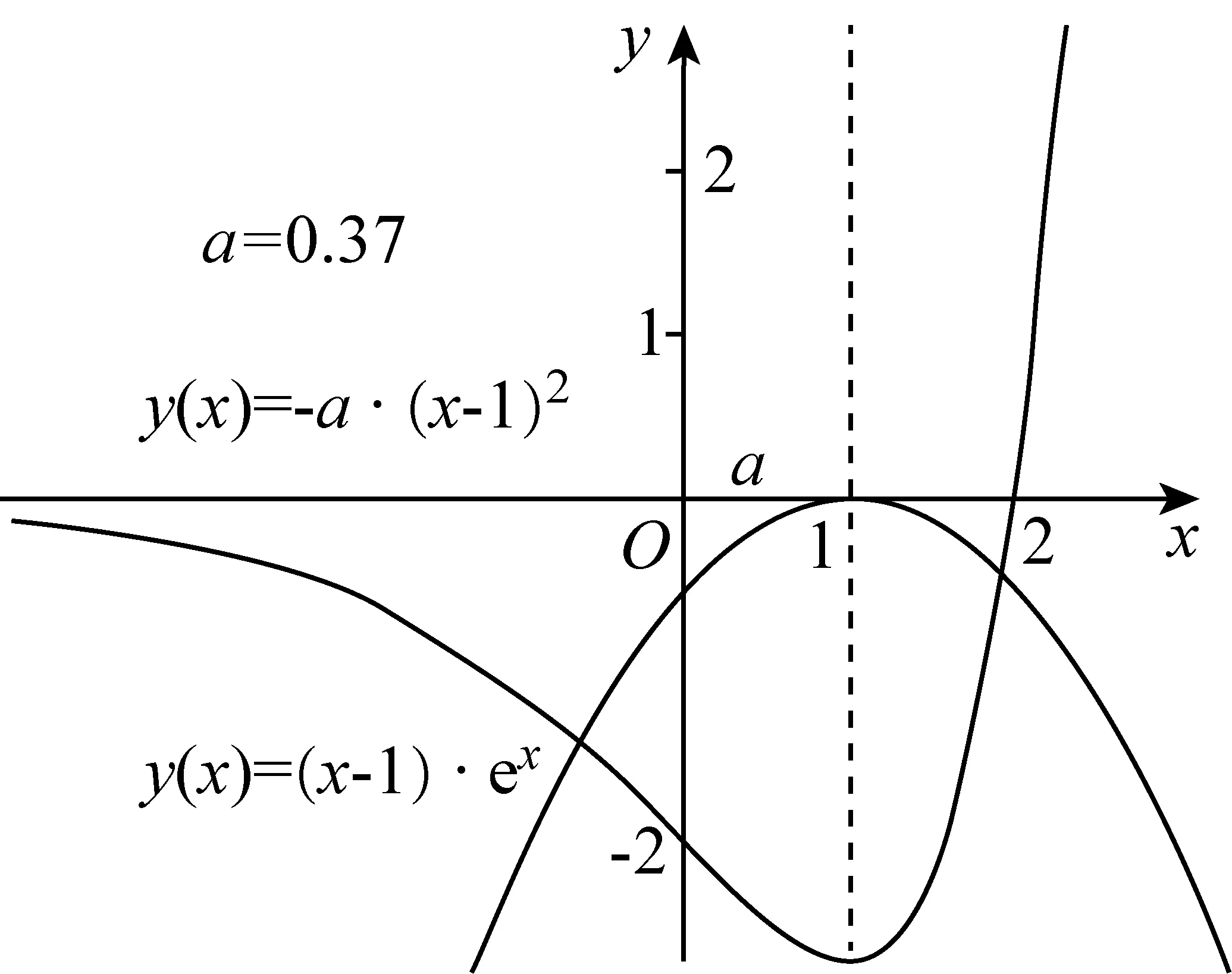
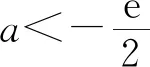
(Ⅱ)由二次函数与对数函数性质可以预感(直觉)到，函数f(x)的值域为R，且当变量x较大时x2+3ax+1是增函数，又lnx也是增函数，所以存在正数m，n(m>n>0)，使得函数f(x)在区间(m，+∞)和(0，n)上是增函数，且当x>m时，f(x)>0，当0

(2)规范解答不失分

令g(x)=2x2+3ax+1(x∈R)，(注意，这里的定义域不是(0，+∞))

因为a<-1，所以g(0)=1>0，

g(1)=2+3a+1=3(a+1)<0，

g(-2a)=2(-2a)2+3a(-2a)+1

=2a2+1>0，

所以g(x)在区间(0，1)与(1，-2a)内各有一个零点，设其分别为s，t，则0

所以g(x)>0⟺xt，g(x)<0⟺s

易知f(x)的增区间为(0，s]和[t，+∞)，减区间为[s，t].

所以f(x)的极大值为f(s)=lns+s2+3as+1.

因为2s2+3as+1=0，所以3as+1=-2s2.

所以f(s)=lns+s2-2s2=lns-s2<0.

所以，当0

从而f(x)在区间(0，t]内没有零点.

又f(-3a)=ln(-3a)+(-3a)2+3a(-3a)+1

=ln(-3a)+1>0，

所以，f(x)在区间(t，+∞)内有且仅有一个零点.

综上所述，当a<-1时，函数f(x)有且仅有一个零点.

(3)解后反思要升华

将f′(x)变形整理后发现，f′(x)的正负完全由其分子2x2+3ax+1决定，通常的方法是考察方程2x2+3ax+1=0的判别式，并由求根公式得到它的两个根，进而得到函数f(x)的单调区间以及f(x)的极值.可以想象的到，这种方法思维过程虽然不难，但运算与表述较为复杂.在上述解法中，我们借助函数零点存在定理，确定了函数g(x)的零点所在的一个恰当区间和零点满足的条件，由此简洁明快地判断出函数f(x)的极大值小于0，使解题过程顺畅、和谐，极具美感.

“数缺形时少直观”，结合函数g(x)的图象(图1)，也能获得一些基本念头，为解题的顺利进行提供了值得努力的方向.

图1

例2(2015，全国Ⅰ卷，文21)设函数f(x)=e2x-alnx.

(Ⅰ)讨论f(x)的导函数f′(x)的零点的个数；

(Ⅱ)略.

(1)谋定思路有方向

图2

(2)规范解答不失分

当a≤0时，f′(x)>0，f′(x)没有零点；

又易知函数f′(x)在(0，+∞)上的图象是连续不断的一条曲线，所以函数f′(x)在(0，+∞)上有且仅有一个零点.

综上，当a≤0时，函数f′(x)没有零点；

当a>0时，函数f′(x)有且仅有一个零点.

解2f(x)的定义域为(0，+∞)，

所以f′(x)=0⟺2xe2x-a=0.

令g(x)=2xe2x-a(x≥0)，则

当a≤0时，g(x)>0在区间(0，+∞)上恒成立，所以f′(x)没有零点；

当a>0时，g(0)=-a<0，

g(a)=2ae2a-a=a(2e2a-1)>0，

又g′(x)=2e2x(x+1)>0，

即g(x)是单调增函数，

且函数g(x)在[0，+∞)上的图象是连续不断的一条曲线，

所以，函数g(x)有且仅有一个零点，

即函数f′(x)有且仅有一个零点.

综上，当a≤0时，函数f′(x)没有零点；

当a>0时，函数f′(x)有且仅有一个零点.

(3)解后反思要升华

本题的解决有两点值得认真体会：

例3(2016，全国Ⅰ卷，理21) 已知函数f(x)=(x-2)ex+a(x-1)2有两个零点．

(Ⅰ)求a的取值范围；(Ⅱ)略．

(1)谋定思路有方向

(Ⅰ)首先利用导数研究函数的单调性与极值．由于f′(x)= (x-1)(ex+2a)，故可以求得f′(x)的零点，进而对参数a进行讨论，得到f(x)的单调性，从而得到f(x)的大致图象，借助图象得到f(x)存在两个零点的条件.

但是，这还得从代数的角度给予严谨论证，即研究函数f(x)的单调性、极值、最值等一般性质，如果函数f(x)有最大(小)值，则其最大(小)值必须大(小)于0，并且在最大(小)值点的左、右两边都存在小(大)于0的函数值．

从而h′(x)>0等价于x<1，h′(x)<0等价于x>1.

所以h(x)在(-∞，1)上是增函数，在(1，+∞)上是减函数．

易知当x<1或10；

当x>2时，h(x)<0.

图3

所以函数y=h(x)的图象如图3所示．

显然，当a≤0时，直线y=a与曲线y=h(x)只有一个交点，所以f(x)只有一个零点；

当a>0时，直线y=a与曲线y=h(x)有两个交点，所以f(x)有两个零点．

从而得到a的取值范围为(0，+∞)．

另外，因为f(x)=(x-2)ex+a(x-1)2=0等价于(x-2)ex=-a(x-1)2，而后边这个等式的等号两边分别是比较简单的函数，所以研究对象得以优化.借助导数研究(x-2)ex的单调性与极值，即可得到他们的大致图象：

图4

图5

结合图4与图5，可以预感到：当a≤0时，f(x)不存在两个零点；当a>0时，f(x)有两个零点．

有了初步的结论，下面的证明就有了一个明确的努力方向了！

(2)规范解答不失分

(Ⅰ)函数f(x)的定义域为R，且

f′(x)=(x-1)ex+2a(x-1)= (x-1)(ex+2a)．

(1)当a=0时，f(x)=(x-2)ex有且仅有一个零点，不合题意．

(2)当a<0时，由f′(x)=0，得x=1或x=ln(-2a)．

所以当x>1时，ex+2a>e+2a≥0，

所以f′(x) ≥0，

所以f(x)在区间(1，+∞)上是增函数，进而函数f(x)在区间(1，+∞)最多只有一个零点．

又x≤1时，

显然f(x)=(x-2)ex+a(x-1)2<0．

所以，此时函数f(x)最多有一个零点，不合题意．

所以f′(x)<0⟺1

即f(x)在(1，ln(-2a))上是减函数；

f′(x)>0⟺x<1或x>ln(-2a)，

即f(x)在(-∞，1)和(ln(-2a)，+∞)上是增函数，

又f(1)=-e<0，

所以当x≤ln(-2a)时，f(x)<0，

所以函数f(x)最多有一个零点，不合题意．

综上，当a<0时，函数f(x)最多有一个零点，不合题意．

(3)若a>0，则ex+2a>0.

所以f′(x)<0⟺x<1，f′(x)>0⟺x>1.

所以f(x)在(-∞，1)上是减函数；在(1，+∞)上是增函数．

所以函数f(x)的最小值为f(1)=-e<0．

又f(2)=a>0，由零点存在性定理知，

函数f(x)在(1，+∞)上有且仅有一个零点．

(下面的目标是寻找小于1的一个实数b，使f(b)=(b-2)eb+a(b-1)2>0.注意到，当b<0时，b-2<0，eb<1，所以(b-2)eb>b-2.所以f(b)=(b-2)eb+a(b-1)2>(b-2)+a(b-1)2.而g(b)= (b-2)+a(b-1)2是一个二次项系数(a)大于0的二次函数，由二次函数性质知，显然存在b∈(-∞，0)，使得g(x)>0.)

因为当x<0时，x-2<0，ex<1，

所以(x-2)ex>x-2.

所以f(x)=(x-2)ex+a(x-1)2

>(x-2)+a(x-1)2=ax2-(2a-1)x+a-2.

设g(x)=ax2-(2a-1)x+a-2(x∈R).

令b=-a-1，则g(b)=g(-a-1)=a(-a-1)2-(2a-1)(-a-1)+a-2=a>0.

因为b<0<1，

又f(x)在区间(-∞，1)上是减函数，

所以函数f(x)在(-∞，1)有且仅有一个零点.

故f(x)在R上有且只有两个零点，满足题意．

综上，a的取值范围为(0，+∞)．

(3)解后反思要升华

在应用函数零点存在性定理时，需要判断函数在区间端点处的正负．当区间端点处的函数值的正负不易判断或所给的区间是开区间时，可考虑考察区间内的特殊值对应的函数值的正负．那么，取怎样的特殊值，为什么取这个特殊值？其实问题很明显，依据之一就是特殊值的选取应以得到需要的函数值正负以及消去参数为主要目的．

解题的目标是需要说明存在一个比1小的实数b，使得f(b)>0，因为f(x)在(-∞，1)上是减函数，所以这个b的选取要尽量小，不妨设b<0，注意到f(x)表达式中含有ex，为了化复杂为简单，可以令b=lnt(t>0)的形式，使其满足f(b)=(b-2)eb+a(b-1)2=(b-2)t+a(b-1)2>0.

那么，上述我们的解法中又是如何想到取b=-a-1的呢？

首先考虑能否将复杂的超越函数f(x)变形为简单的多项式函数，并且这个多项式函数小于f(x).这应该从f(x)中的超越式入手，即(x-2)·ex能否被比它小的代数式替代？显然当x<0时，x-2<0，ex<1，所以(x-2)ex>x-2.所以只需寻找一个负实数b，使g(b)=(b-2)+a(b-1)2>0即可.对于二次项系数大于0的二次函数g(x)=ax2-(2a-1)x+a-2来说，这是完全可以做得到的！