思想立意 发展数学核心素养①

林新建

(福建省漳州第一中学 363000)

在过去的教学活动中，教师可能更关心如何教，但基于数学核心素养的教学，更多地需要关心学生如何学，需要知道学生的认知水平和认知过程.

一个理想的教学过程大概可以描述如下：把握数学知识的本质，把握学生认知的过程；创设合适的教学情境，提出合适的数学问题；启发学生思考，鼓励学生与他人交流；让学生在掌握知识技能的同时，理解数学知识的本质；感悟数学的思想，形成和发展数学核心素养.

这里的关键是“感悟数学的思想，形成和发展数学核心素养”，本文从一道试题解答的探寻与启示入手，就“思想立意”在“感悟数学思想，形成和发展数学核心素养”上的作用与途径作一探析，以飨读者.

1 探寻与启示

例1(2011年高考新课标卷Ⅰ理科16题)

解析本题是三角形求解问题，解决问题的通法是“知三求三”，即已知三边求三角，或已知两边一角求另一边两角，或已知一边两角求另两边一角.

但直观题目只给出一边一角，显然条件少了，无法直接运用通法“知三求三”加以解决，怎么办？

此时，若能立意于函数思想，则不难发现这是最值求解问题，需要引入变量，构造出待求最值关于这个变量的函数，问题可轻松获得解决.

为此，不妨设∠A=θ，则∠C=120°-θ.

进而得AB+2BC=2sin(120°-θ)+4sinθ

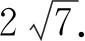
评析由于变量的引入，我们凑足了三个量，从而可以运用通法“知三求三”将问题轻松予以解决.在这里，思想的立意是问题获得解决的关键，正是缘于函数思想的立意，我们自然地引入了变量，构造出待求最值关于这个变量的函数，使得问题轻松获得解决.

为什么有许多学生解决不了一些并不复杂甚至是简单的数学问题呢？除了极少数学生不知道相应的数学知识外，绝大部分学生不是不会方法，而是由于没有站在思想的高度来思考和引领方法，或者是因为思想不明确而想不起来用什么方法来处理问题.

因此，指导学生立意于思想，让他们在“润物细无声”中逐步领悟数学思想，并用其作为指导来引领问题的解决就显得尤为重要了.

2 思想立意：基于“四基”的数学教学活动

传统数学教育的“双基”是指基础知识和基本技能，要求基础知识扎实，基本技能熟练.2001年开始的课程改革，在传统的“双基”这个一维目标的基础上提出三维目标，这就是：知识技能、过程方法、情感态度价值观，这里所说的情感态度价值观就是现在核心素养所说的态度或者必备品格.

但是，三维目标中所说的“过程方法”没有成为目标，这是因为在描述“过程方法”时使用的行为动词是“经历”、“体验”、“探索”，并没有说明通过这些“过程”让学生获得什么.为此，在修订数学课程标准时，把“过程”目标表述为：通过学生参与其中的数学教学活动过程，让学生感悟数学的基本思想，积累数学思维和实践的基本经验.

这就把传统数学教育的“双基”发展为“四基”，并且强调：“四基”的提出是在传统的“双基”的前提下，加上了基本思想和基本活动经验，目的是通过数学的学习，学生不仅把数学作为一种技术和手段，还要学会思考，逐步具有数学抽象的能力和逻辑推理的能力.

例2(2014高考课标全国卷Ⅰ第8题)

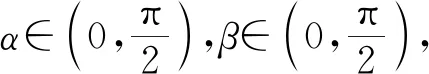
解析本题是一道考查基础知识与基本方法的好题，依据对公式的灵活使用，可得到几种常规解法，这里仅举一例.

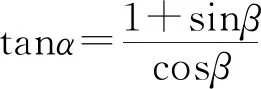
sinαcosβ-cosαsinβ=cosα，

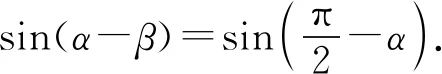
但若教学仅止步于此，可以看到，这样的教学活动无法让学生理解数学知识的本质，更不可能感悟数学的基本思想，形成和发展数学的核心素养.为此必须创设思想立意的活动，引领学生立意于思想解决问题.

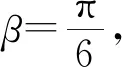
在这里，“特殊与一般思想”的立意是问题获得轻松解决的关键.正是由于“特殊与一般思想”的立意，我们“依据逻辑规则从特殊到一般与一般到特殊地进行推理”，将问题轻松予以解决，在这个过程中，逻辑推理等能力得到了发展.

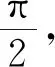
在这里，“有限与无限思想”的立意是问题获得轻松解决的关键.正是由于“有限与无限思想”的立意，我们“从事物的具体背景中抽象出了一般规律”，并依据规律将问题轻松予以解决，在这个过程中，数学抽象等能力得到了发展.

可见，“思想立意”能让学生感悟知识所蕴含的数学基本思想，积累数学思维和实践的经验，同时提升和发展逻辑推理与数学抽象等能力，是基于“四基”的数学教学活动.

3 思想立意：数学核心素养的发展要领

由于数学核心素养是“四基”的继承和发展，所以“四基”就是发展学生数学核心素养的有效载体，数学教学中应当引领学生立意于思想解决问题，在问题解决的过程中培养和发展数学核心素养.

3.1 立意“特殊与一般思想”，发展数学抽象、逻辑推理核心素养

通常在理解题目阶段，需要对题目中的隐含条件和信息进行发掘，将抽象变具体，将隐含变清晰.

而如何将“抽象变具体、将隐含变清晰”呢？这就需要立意“特殊与一般、有限与无限”等思想，才能“从事物的具体背景中抽象出一般规律和结构”，进而“从一般到特殊和特殊到一般地予以推理”，这是数学抽象和逻辑推理的前提.

例3(2010年高考新课标卷Ⅰ理科11题)

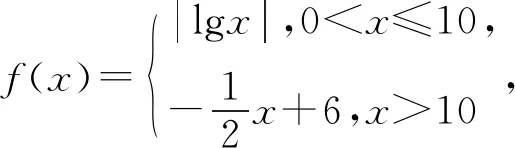
A．(1,10) B．(5,6)

C．(10,12) D．(20,24)

例4(2013年高考新课标卷Ⅰ理科11题)

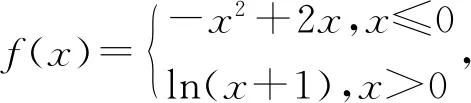
A．(-∞,0] B．(-∞,1]

C．[-2,1] D．[-2,0]

解析本题按常规方法求解也较为繁琐，若能立意于特殊与一般思想，同样能从问题的具体背景中抽象出一般规律：“|f(x)|≥ax”对于变量x在R中的任意取值都成立，则可将变量特殊化予以求解，如取x=-1，得a≥-3，排除选项A、B；再取x=1，得a≤ln2，排除选项C，故正确选项为D.

评析可以看出，由于特殊与一般思想的立意，我们“从事物的具体背景中抽象出一般规律和结构”，进而对问题“从一般到特殊和特殊到一般地予以推理”，从而将问题轻松予以解决.在这个抽象和推理的过程中，“数学抽象、逻辑推理”等核心素养得到了发展.

3.2 立意“有限与无限思想”，发展逻辑推理、直观想象核心素养

如何引领学生思考“按照怎样的线索、用什么方法去研究问题、解决问题？”这需要立意“有限与无限、数形结合”等思想，才能“感知事物的形态变化与运动规律”，进而“依据逻辑规则推出一个新的命题”，这是逻辑推理、直观想象的基础.

如上例3，若能立意于有限与无限思想，则能从问题的具体背景中感知出事物的形态与变化：b、c随着a的变化而变化，a、b的变化具有无限性特征，它们可无限趋近于1，则可将变量极限化予以求解：令a→1，则f(a)→0，从而由f(b)=f(c)→0知b→1，c→12，abc→12，验证选项即知正确答案为C.

例5(2015年高考新课标卷Ⅰ理科16题)

在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是________.

解析本题直接求解难度较大，若能立意于有限与无限思想，则能从问题的具体背景中感知出事物的形态与变化：动点D的变化具有无限性的特征，它可无限趋近于点A，也可无限趋近于点C，则可将问题极限化予以求解：

令D→A，则∠B=∠C=75°，∠A=30°，

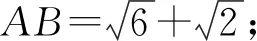
令D→C，∠A=∠B=75°，∠C=30°，

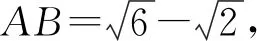
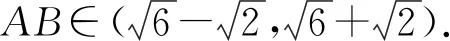
评析可以看出，由于有限与无限思想的立意，我们“感知出事物的形态变化与运动规律”，进而对问题“从一般到特殊和特殊到一般地予以推理”，将问题轻松地予以求解.在这个直观和推理的过程中，“逻辑推理、直观想象”等核心素养得到了发展.

3.3 立意“函数与方程思想”，发展数学建模核心素养

如何引领学生思考“面对一个新的研究对象，从哪些角度发现和提出值得研究的问题？”这需要立意“函数与方程、化归与转化”等思想，以便“发现模型、构建模型，进而借助模型解决问题”，这是数学建模、数据分析的关键.

如上例5，若能立意于函数思想，则能从数学的视角发现这是最值与取值范围问题，应构建出关于目标函数的函数模型，问题不难获解.

为此，不妨设∠BAC=θ，则∠BCA=105°-θ，

由θ<75°及105°-θ<75°知30°<θ<75°.

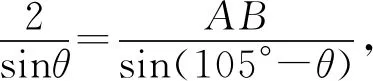
从而知

例6(2010年高考新课标卷Ⅰ文科16题)

在△ABC中，D为BC边上一点，BC=3BD，

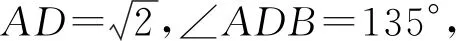
解析本题是三角形求解问题，无论在哪个三角形中都因条件不足无法直接运用通法“知三求三”予以求解.

若能立意于方程思想，则能从数学的视角发现这是变量求解问题，应构建出关于这个变量的方程模型，问题不难获解.

为此，可设BD=x，则DC=2x.

在△ADC中，由余弦定理得

化简得b2=2+4x2-4x.

在△ADB中，由余弦定理得

化简得c2=2+x2+2x.

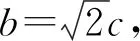
所以2+4x2-4x=2(2+x2+2x)，

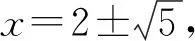
评析可以看出，由于函数与方程思想的立意，我们“从数学的视角发现问题、提出问题、分析问题”，进而“构建模型、求解结论”，将问题轻松予以求解.在这个抽象和建模的过程中，“数学建模、数学抽象”等核心素养得到了发展.

4 结束语：“立意”恒久，“素养”终成

经验之中有规律，是我们认识问题的一般过程和方法，也阐明了一个简单但很深刻的教学原理：经验是具体的，规律则是抽象的.规律不是从天而降的，而是从具体经验中经过不断归纳、概括才能得到的.

如何才能培养学生“从经验中发现规律”的能力呢？这需要培养“思想立意”的意识与习惯，养成“从一般规律的高度考察具体事例”的意识和“透过现象看本质”的习惯.

这是观念问题，是思维习惯问题，也是思想方法问题.这是一个长期的、潜移默化的过程，是逐渐养成的一种思维习惯，这个习惯日积月累就形成了数学素养.