不确定切换系统的有限时间稳定性1
陈国培,杨 莹
(惠州学院 数学与大数据学院,广东 惠州 516007)
有限时间稳定性是一个比渐近稳定性更强的稳定性概念,它表示系统是李雅普诺夫稳定的且系统状态是有限时间收敛的.
由于有限时间稳定性在理论和应用中的重要作用,人们已研究了若干类主要系统的有限时间稳定性及其稳定化问题.文献[1]针对非线性系统,给出了系统的有限时间稳定性判据以及连续的收敛时间函数.文献[2]研究连续线性系统的输出稳定化问题,利用LMI的最优解构造出输出反馈控制器使闭环系统达到有限时间稳定.文献[3]针对一类二阶非线性系统,研究其反馈镇定问题,提供了几类全局有限时间状态反馈的镇定方法,实现闭环系统的有限时间稳定化.文献[4]通过构造切换控制策略,实现一类非线性系统在输入饱和情况下的有限时间稳定化.文献[5]运用加幂积分和嵌套饱和的方法设计控制器,实现了闭环系统的全局渐近稳定化和有限时间稳定化.文献[6]针对随机多智能体系统,利用李雅普诺夫 有限时间随机稳定性理论,设计出目标状态和环绕半径的估计器以及分布式环绕控制器,确保系统有限时间稳定.
值得注意的是,关于具有不确定性的非线性切换系统的有限时间稳定性研究鲜有报道,而且现有结果对系统都有一个要求,即:系统的李雅普诺夫函数在整个时间区间上必须是单调减少的,该要求限制了这些已有结果在实际当中的应用.对于许多实际系统,如:周期变化的系统,这个要求是难以满足的.为了放松这一限制,本文将基于有限时间稳定性理论给出不确定非线性系统的有限时间稳定性条件.然后,利用所获得的条件结合所构造的李雅普诺夫函数,给出具有不确定性的非线性切换系统的稳定性条件.
1 不确定非线性系统的有限时间稳定性
考虑如下的不确定非线性系统:

定义 1[1]系统(1)在满足下列条件时是有限时间稳定的:
现有的有限时间稳定性结果(即:文献[1]的定理4.2以及文献[2]的定理2)要求系统的李雅普诺夫函数在整个时间区间上必须单调减少,但这一要求在实际应用中是难以满足的.为了放松这一限制,我们利用非单调李雅普诺夫函数技术给出如下的有限时间稳定性条件.
定理1对于系统(1),若存在连续函数()g t和()h t,以及常数01<<a满足如下条件:
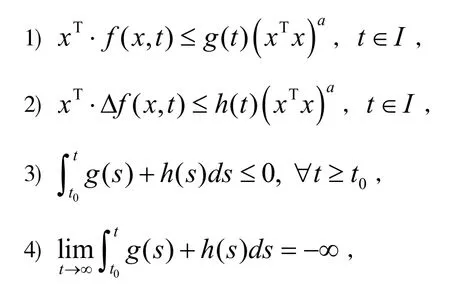
则系统(1)全局有限时间稳定.
证:对系统(1),构造李雅普诺夫函数由条件1)-2),有:

即:

对(2)式两边从0t到t进行积分可得:


结合(3)和(4)式,有:

2 主要结果
在前述结果的基础上,进一步研究不确定切换系统的有限时间稳定性.考虑如下的不确定切换系统:

其中:x(t)∈Rn,切换律,N为子系统的个数.根据切换律()tσ,我们有切换序列其中第ki个子系统在时间内被激活.对于每一个iQ∈,函数连续且
利用所获得的条件结合随后构造的李雅普诺夫函数,可推出系统(6)的有限时间稳定性条件.
定理 2对于系统(6),若存在连续可微函数,连续函数以及常数01<<a满足如下条件:

则系统(6)在切换律()tσ的作用下是全局有限时间稳定的.
证:对任意的由条件2)-3)我们有:

即:

对(7)式两边从kt到t进行积分可得:


再由 ()V x的正定性及定理1的类似证明,可知系统(6)是李雅普诺夫稳定的且有限时间收敛,即:系统(6)在切换律()tσ的作用下为全局有限时间稳定.
3 数值例子
考虑如下的不确定切换系统:


4 结语
本文针对具有不确定性的非线性切换系统,探讨其有限时间稳定性.首先,基于有限时间稳定性理论给出不确定非线性系统的有限时间稳定性条件.然后,利用所获得的条件结合所构造的李雅普诺夫函数,给出具有不确定性的非线性切换系统的稳定性条件.

