利用子列极限证明数列上下极限的性质1

唐建国，刘幸茹

（惠州学院 数学与大数据学院，广东 惠州 516007）

数列上下极限的等价定义比较多，文[1]给出了三种定义的等价证明，文[2]列出了七个等价定义.在由这些定义推导数列上下极限的性质时，按不同的定义有不同的证明方法.在构建数列上下极限的理论体系时，通常选取较易构建逻辑体系的定义作为出发点或研究的起点，这样会给理论体系的建立带来很多方便.本文试图选取子列的最大最小极限作为数列上下极限的定义，证明数列上下极限的性质.与其它几个等价定义相比，该定义具有很好的形象性和直观性，对理解数列上下极限的性质有很大帮助，并能从已有性质出发发现和建立一些新的性质.

1 数列上下极限的定义及简单充要条件

定义1[1]设｝是一个实数列，它的上下极限分别定义为的所有收敛子列的最大极限，的所有收敛子列的最小极限.

性质1的充分必要条件是:存在的收敛子列，使得，且对于的任何收敛子列有的充分必要条件是:存在的收敛子列 }{knx ，使得，且对于的任何收敛子列，有

性质2[3]的充分必要条件是:任给0＞ε,存在0＞N，使得当Nn≥时，有ε+＜axn，且存在子列 }{knx ，使得的充分必要条件是:任给0＞ε,存在0＞N，使得当Nn≥时，有ε-bxn＞，且存在子列使得

性质3[3,10]的充分必要条件是

2 数列上下极限的四则运算性质

性质4[4]

证明根据性质1，存在 }{nx 的收敛子列 }{knx ，使得，且对于 }{nx 的任何收敛子列有，由此可得且，再利用性质1得，

在前式中nx用nx- 来代，即得

性质5

证明对于 0=c ，结论显然成立.

当0＜c时有0＞-c，根据性质4及已得结果有

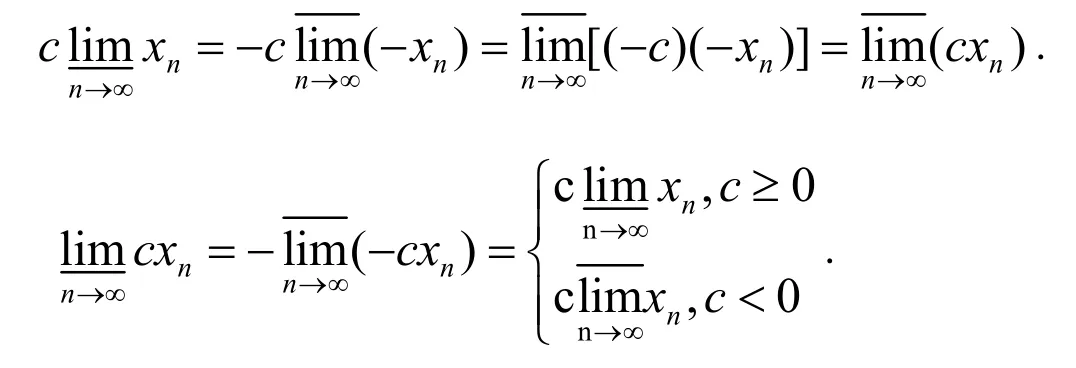
性质6

证明根据上极限的定义，存在 }{nx 的收敛子列 }{knx ，使得

故第一个等式成立.由性质4得，

性质7[3]若

证明根据上极限的定义，存在 }{nx 的收敛子列 }{knx ，使得

数列 }{kny 存在收敛子列 }{jkny ，此时有，因此

根据下极限的定义，存在 }{ny 的收敛子列 }{kmy ，使得

数列 }{kmy 存在收敛子列 }{jkmy ，此时有，因此

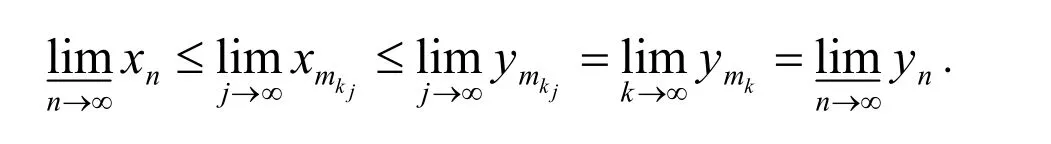
性质8[4]若存在，则

证明根据上极限的定义，存在的收敛子列，使得存在收敛的子列所以

3 数列上下极限的计算公式及其它性质

性质16设 }{knx 是数列 }{nx 的任一子列，则

证明根据上极限的定义，存在 }{knx 的收敛子列 }{jknx ，使得

性质17[6,9,11]设 }{nx 为有界数列，

（1）若 )(xf 在实数集R上连续，且单调增加，则

（2）若 )(xf 在实数集R上连续，且单调减少，则

证明（1）根据上极限的定义，存在的收敛子列，使得由于有界，因而其子列 }{knx 也有界.根据有界数列必有收敛的子列知，存在 }{knx 的收敛子列 }{jknx ，使得又 ()f x在实数集R上连续，因而在点0x连续，因此

另一方面，根据上极限的定义，存在 }{nx 的收敛子列 }{kmx ，使得

由于 }{nx 有界，因而其子列 }{knx 也有界.根据有界数列必有收敛的子列知，存在 }{knx 的收敛子列 }{jknx ，使得又 ()f x在实数集R上连续，因而在点0x处连续，

另一方面，根据下极限的定义，存在 }{nx 的收敛子列 }{kmx ，

（2）由 ()f x单调减少知， ()f x- 单调增加.

由此可得

故结论成立.

下面给出性质17的逆命题.

性质18设 }{nx 为有界数列，

（1）若 ()f x在实数集R上连续，单调增加，且

（2）若 ()f x在实数集R上连续，单调减少，且

证明（1）由于 ()f x在实数集R上连续，且单调增加，因此 ()f x在实数集R有反函数1()f x-，且1()f x-实数集R上连续，单调增加.所以根据性质17得，

性质19[3]若

证明若存在，则

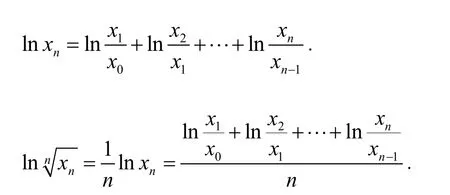
根据斯托尔茨公式

在这种情形结论成立.

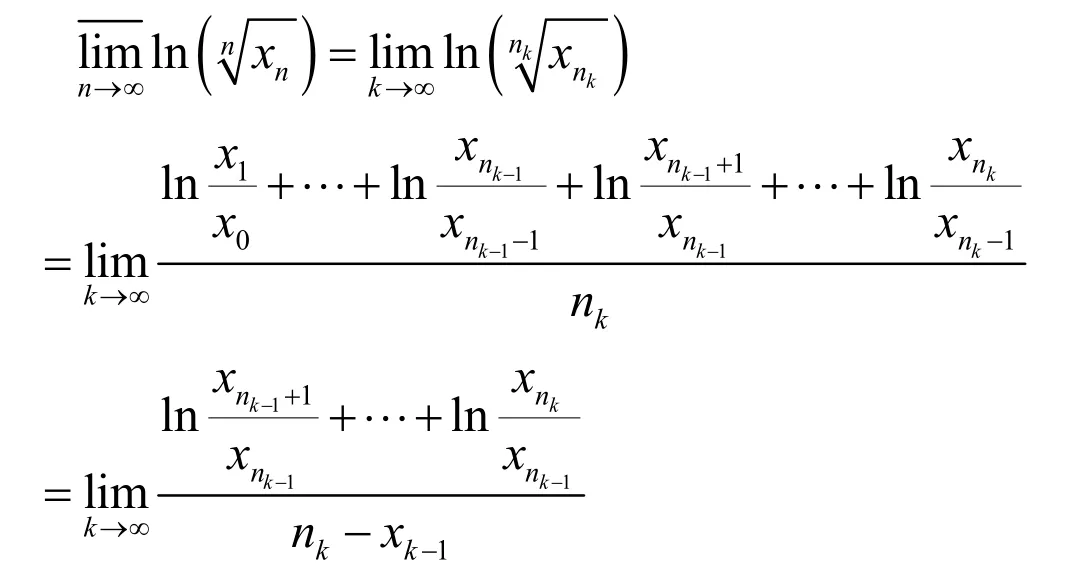
根据性质2，任给0＞ε，存在0＞N，使得当Nn≥时，总有

由ε的任意性及性质18知，结论成立.

性质20[7]设是两个实数列，若(i)严格单增，(ii)

证明若存在，根据已知条件及斯托尔茨公式，不存在，则必

由ε的任意性可知，上极限不等式成立.同理可得，下极限不等式成立.

性质21[7]设严格单调递减，则

证明若存在，根据已知条件及斯托尔茨公式，不存在，则必

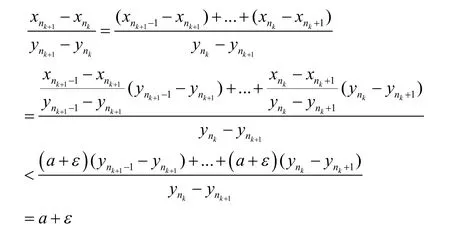
由ε的任意性可知，上极限不等式成立.同理可得，下极限不等式成立.

4 数列上下极限与子列上下极限的关系

引理1[8]设，则，这里'A={A的所有聚点}.

这一结果还可以进一步推广到有限个集合的情形.

引理2设

由引理1和引理2即可得以下性质.

性质22设是数列，若将分成两个子列和，则

性质23设是数列，若将分成m个子列则必存在子列和子列使得

5 结语

数列上下极限是数列极限概念的推广与延伸,一般数学分析教材很少涉及这一内容,甚至也没有将其列入教材作为选讲内容 .但数列上下极限在数学的很多分支有着广泛的应用,例如实变函数 中§4.1定理6:可测函数列的上下极限仍是可测函数,§5.3定理6法图(Fatou)引理:非负可测函数列下极限的勒贝格积分不超过其勒贝格积分的下极限,以及§5.4勒贝格控制收敛定理(定理5)的证明过程中都需要用到数列的上下极限.本文利用子列极限证明数列上下极限的23条性质,今后将继续探索数列上下极限的新性质及其应用.