非结合代数的嵌入定理*

李 羽

（惠州学院 数学与大数据学院，广东 惠州 516007）

Higman,B.H.Neumann和H.Neumann[1]证明了每一个可数群都可嵌入到一个二元生成的群. Malcev[2]证明了每一个可数生成的结合代数可以嵌入到二元生成的结合代数. Shirshov[3]和Evans[4]分别证明了李代数和半群的相似结果. Neumann证明了每一个非结合代数都可以嵌入到一个非结合可除代数, 使得任意方程=,=,≠0在后者中有解. 任何可除代数都是单的. Cohn[5]证明了每一个不带零因子的结合环都可以嵌入到一个不带零因子的单结合环中使得任意方程-=,≠0在后者中有解. Skornyakov[6]证明了每一个没有零因子的非结合代数都可以嵌入到一个没有因子的非结合除代数中. Ivanov[7, 8]证明了Ω-代数的相同结果. Cohn[5]证明了每一个李代数都可以嵌入到一个可除李代数中. Shutov[9]和Bokut[10]证明了每一个半群都可以嵌入到一个单半群, Bokut[11]证明了每一个结合代数都可以嵌入到一个单结合代数, 从而使得任何方程=,≠0在后者中都是可解的. Bokut[12, 13]证明了每一个李（非结合, 可交换, 反交换）代数可以嵌入代数闭（特别地, 单的）李（非结合, 交换, 反交换）代数中, 使得系数在中的任意方程(,…,)=0在中有解(上的方程是与相应自由代数()的自由积的一个元素).

Bokut在[11, 14, 15]中证明了任何结合(李)代数都可嵌入到一个结合(代数闭李)单代数中, 该代数是一个具有某些基数条件的四个(李)子代数的和. 特别地, 任何可数结合(李)代数都可嵌入到一个有限生成的单结合(李)代数中. Goryushkin[16]证明了任何可数群都可以嵌入到一个二元生成的单群. 2010年, Bokut,Chen和Mo[17]利用Gro¨bner-Shirshov基, 证明了在结合微分代数, 结合Ω-代数和结合λ-微分代数中, 每个(可数生成的)代数都可以嵌入到一个单（二元生成）代数中； 他们还证明在可数域k上的每个可数生成代数都可以嵌入到以下几类单的二元生成代数中: 结合代数, 半群, 李代数, 结合微分代数, 结合Ω-代数, 结合λ-微分代数. 2011年,Bahturin和Olshanskii[18]证明了, 任何有限生成的不变形的结合代数(李)都可以嵌入到不变形的二元生成结合(李)代数中.

2017年, Li和Mo[19]证明了可数域上每一个可数生成的非结合代数都可以嵌入到一个二元生成的单非结合代数. 同一年, 他们[20]证明了每个可数生成的结合代数(李代数)都可以嵌入到一个二元生成的单结合代数(李代数)中. 2017年, Mo,Zhao和Pan[21]证明了每一个可数生成的结合微分代数(Ω-代数, 结合λ-微分代数)都可以嵌入到一个二元生成的单结合微分代数(Ω-代数, 结合λ-微分代数)中. 2019年Mo[22]证明了每一个可数生成的-代数(反交换代数)都可以嵌入到一个二元生成的单-代数（反交换代数）.

本文利用Shirshov[23]的非结合代数的Gro¨bner-Shirshov基理论证明了域上每一个可数生成的非结合代数都可以嵌入二元生成的单非结合代数.

1 非结合代数的合成钻石引理

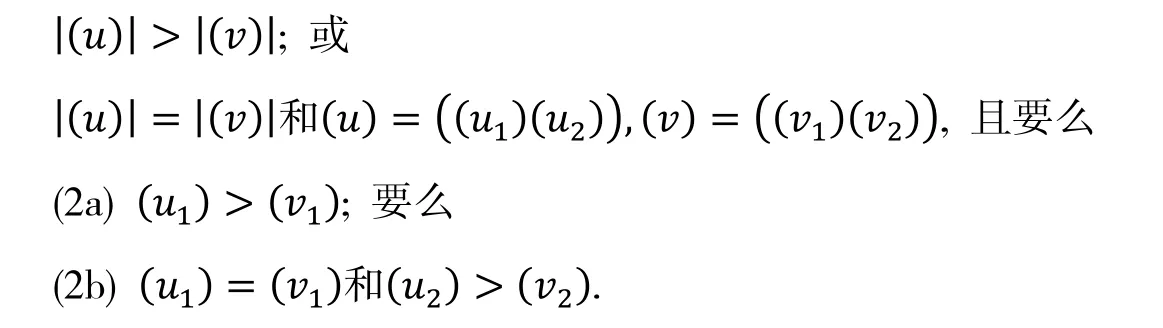
我们称这个序为次数字典序, 整篇文章我们都用这个序. 设是一个域, M(X)是上由生成的自由非结合代数. 对于每一个非零多项式∈(),可唯一地表示成

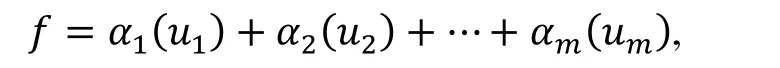
定义1令为一个首1多项式构成的集合. 每一个多项式叫做一个度为1的字. 假设是一个长度为的字,是一个次数为的非结合字. 那么叫做长度为+的字.

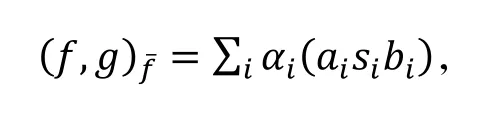
定义 2([23]) 令是一个首 1多项式构成的非空集合,＞是**上的次数字典序. 如果任意的合成模平凡的, 那么叫做一个基.

引理1令为一个首一多项式构成的集合且

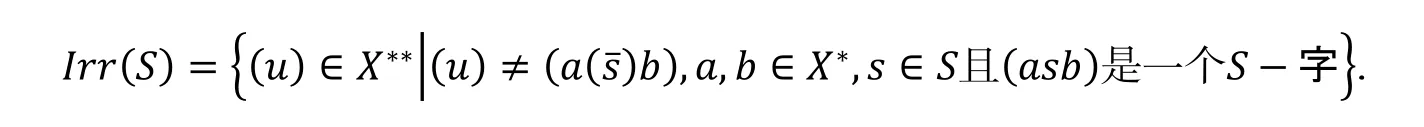
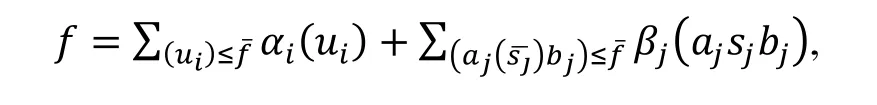
定理1([23], 非结合代数的合成钻石引理) 令是一个首1多项式构成的非空集,是M(X)的由生成的理想且＞是**上的次数字典序. 则下面的表述是等价的:

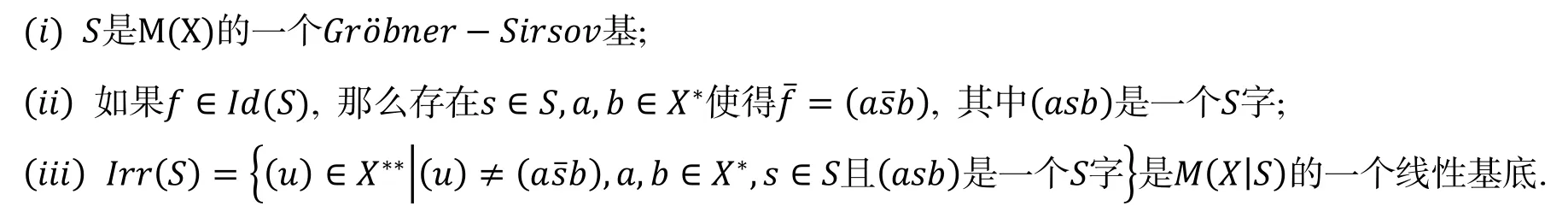
2 二元生成的单非结合代数

定理2域上每一个可数生成的非结合代数可以嵌入到一个二元生成的单非结合代数.

证明设是域上的一个非结合代数且的一个-基, 乘法表为其中是的一个线性组合. 那么可以用生成元和关系表示成

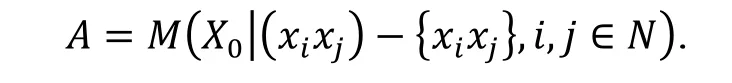
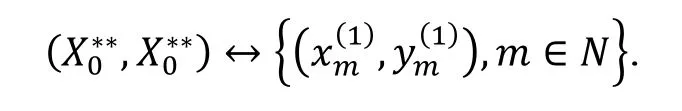
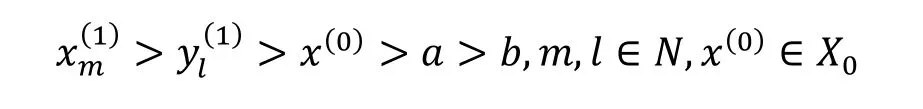
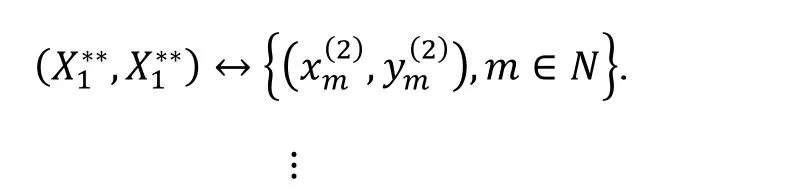
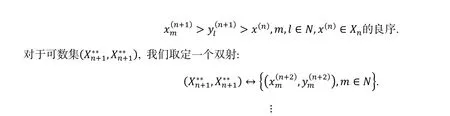
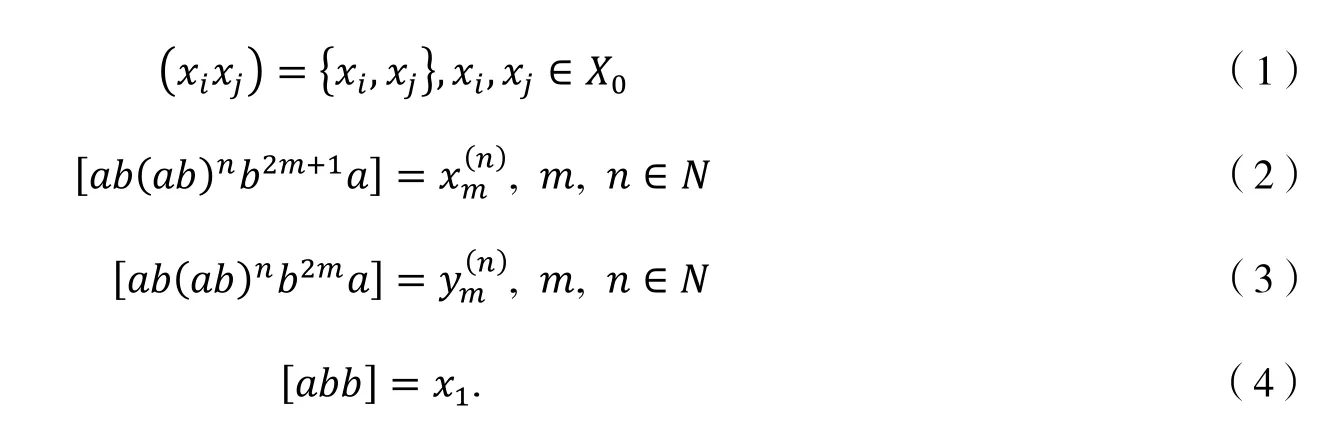
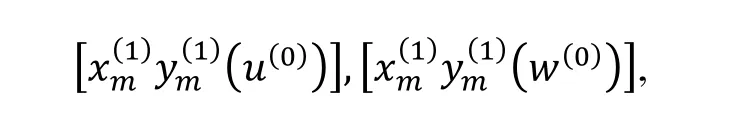
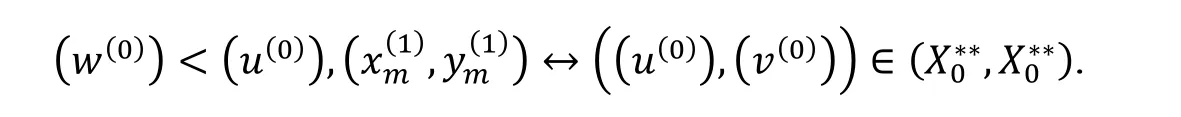
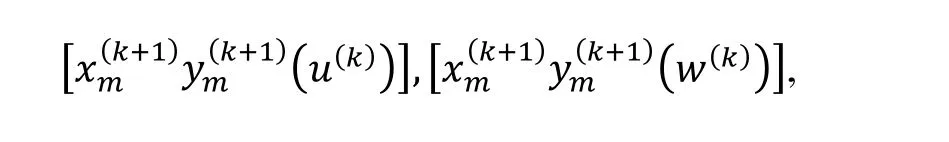
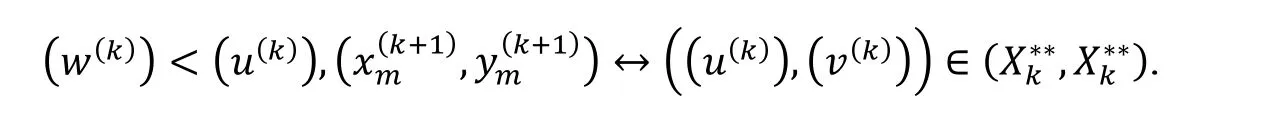
那么B的另一部分关系为

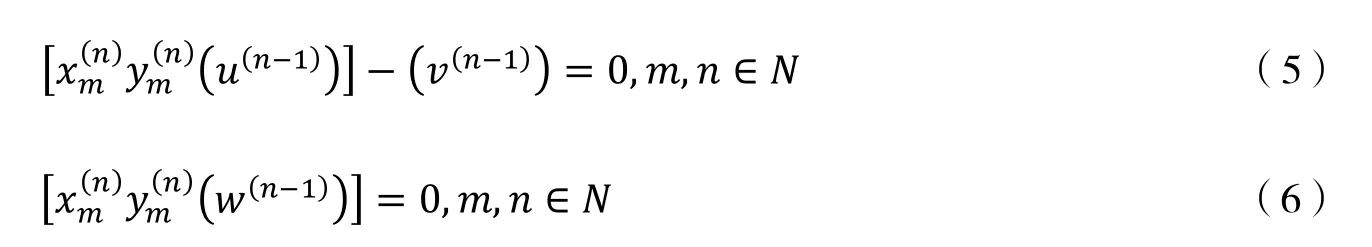
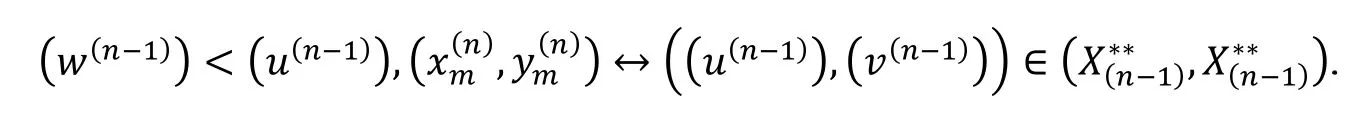
根据引理1 , B的每一个元素都可以表示成标准字的线性组合. 用表示由关系(1)-(6)组成的集合. 易见中是没有合成的. 因此,是()的一个非结合基. 这意味着可以嵌入 B. 由(2)-(5)可得, B 由生成.

假设Bgf∈,且

注释：

①这里, 我们将s看成一个新的字母而(asb)看成是新的字母表X∪{s}上的一个字.