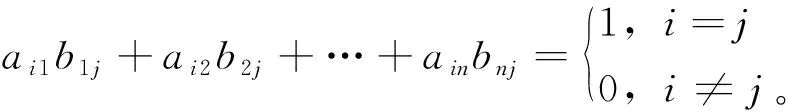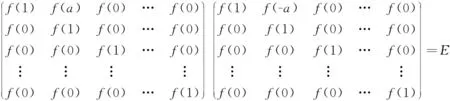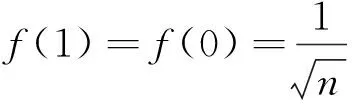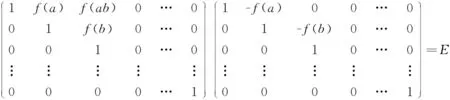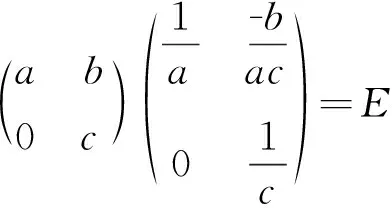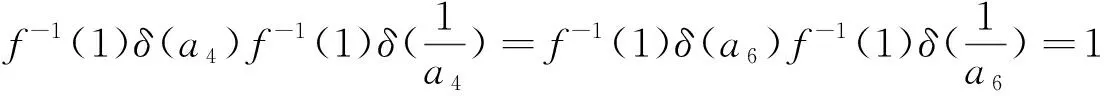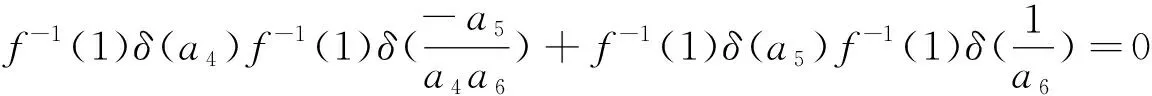上三角矩阵空间的保持逆矩阵的函数

樊玉环,袁海燕,魏 喆

(黑龙江工程学院 理学院，黑龙江 哈尔滨 150000)

目前研究保持问题的基本思想是削弱已有结果的条件，例如文献[1]～[7]；或是改变已有结果的映射形式或映射所作用的集合，例如文献[8];或是寻求新的不变量，例如文献[9]～[12]。关于函数保持的结果目前不是很多，本文是在文献[9]的基础上，改变已有结果所作用的集合，刻画了特殊矩阵空间，即上三角矩阵空间保持逆矩阵函数的形式。

1 符号及基本概念

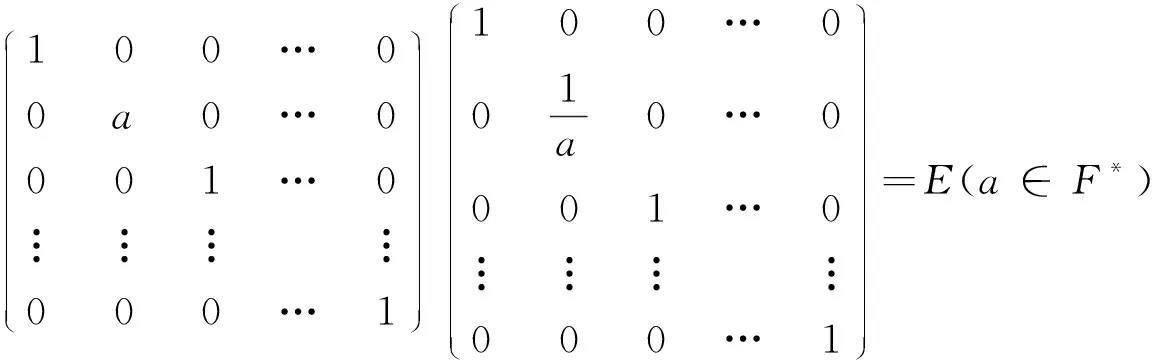
设F是特征不为2的域,F*表示F/{0},Tn(F)为F上所有n阶上三角矩阵的全体,E为单位矩阵，A=(aij)，Af=(f(aij))。

定义1.1[15]若f:F→F满足f(a+b)=f(a)+f(b),f(ab)=f(a)f(b)。则称f:F→F是同态。

定义1.2[16]设n阶矩阵A=(aij)n×n，若存在n阶矩阵B，满足AB=BA=E，称B为A的逆矩阵。

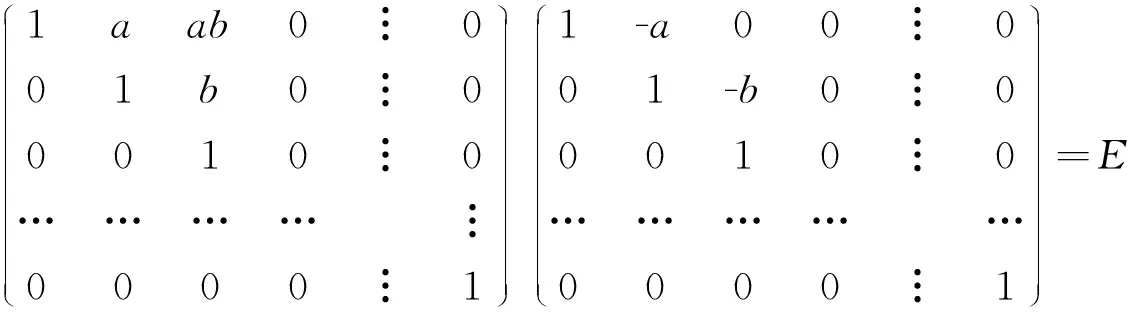
定义1.3[8]若f:F→F满足AB=E，∀A、B∈Tn(F),则AfBf=E。则称函数f:F→F是n阶上三角矩阵空间的保持逆矩阵的函数。

2 基本结论

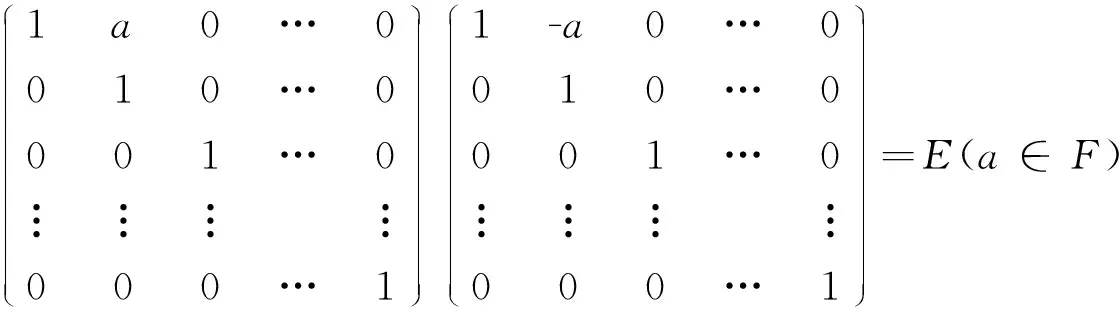
定理2.1f是n(n≥4)阶上三角矩阵空间的保持逆矩阵的函数的充要条件是f=δ，δ是域F上的满足δ(1)=1单的自同态。

证明首先证明充分性

设A,B∈Tn(F)，记A=(aij),B=(bij)，当j

由Af的定义，可知AfBf的(i,j)元为f(ai1)f(b1j)+f(ai2)f(b2j)+…+f(ain)f(bnj)。

若f=δ，由δ是域F上满足δ(1)=1单的自同态,知

f(ai1)f(b1j)+f(ai2)f(b2j)+…+f(ain)f(bnj)

=δ(ai1)δ(b1j)+δ(ai2)δ(b2j)+…+δ(ain)δ(bnj)

=δ(ai1b1j+ai2b2j+…+ainbnj)

下面再证明必要性

由Af的定义，可知

从而

f2(1)+f(a)f(0)+(n-2)f2(0)=1

(1)

f2(1)+(n-1)f2(0)=1

(2)

f(1)f(a)+f(1)f(-a)+(n-2)f2(0)=0

(3)

2f(1)f(0)+(n-2)f2(0)=0

(4)

由(1)、(2)可知

f(a)f(0)=f2(0)

(5)

由(3)、(4)可知

f(1)f(a)+f(1)f(-a)=2f(1)f(0)

(6)

f(0)=0

(7)

将(7)式代入(3)式，有

f(-a)=-f(a)

(8)

由Af的定义及(7)式，可知

可得

(9)

由Af的定义、(7)式及(8)式，可知

可得

f2(1)-f(1)f(a+1)+f(a)f(1)=0

(10)

利用(9)式可得f(1)≠0，从而

f(1)+f(a)=f(a+1)

(11)

由Af的定义及(8)式，可知

可得

f(a)f(b)=f(ab)

(12)

令δ=f，下面证明δ是域F上的单的自同态。

应用(12)式得δ(ab)=f(ab)=f(a)f(b)=δ(a)δ(b)

即得

δ(ab)=δ(a)δ(b)

(13)

应用(11)、(12)式及(13)式得

即得

δ(a+b)=δ(a)+δ(b)

(14)

由(9)式可得

f(a)≠0,∀a∈F*

(15)

若δ(a)=δ(b), 则f(a)=f(b)，f(a)-f(b)=0， 应用(8)式f(a)+f(-b)=0，即δ(a)+δ(-b)=0， 应用(14)式δ(a-b)=0， 即f(a-b)=0， 应用(15)式得a=b。

从而δ是域F上的单的自同态。

在(12)式中，令a=b=1， 可得f2(1)=f(1)，再由(2)式及(7)式可得f(1)=1， 即δ(1)=1，从而f是n阶上三角矩阵空间的保持逆矩阵的函数一定能得到f=δ，δ是域F上的满足δ(1)=1单的自同态。

定理2.2f是T2(F)保持逆矩阵的函数充要条件是f是非零乘法奇函数。

证明首先证明充分性

由于f是非零的乘法奇函数，故

f(xy)=f(x)f(y)

(16)

f(-x)=-f(x)

(17)

在(16)中，令y=1，则f(x)=f(x)f(1)，由于f是的非零映射， 故f(x)≠0， 从而

f(1)=1

(18)

下面证明必要性

通过矩阵的运算及f的定义可得

f(0)=0

(19)

(20)

(21)

由(20)、(21)式可得

f(-ac)=-f(a)f(c)

(22)

在(21)式中令a=c=1， 可得

f(-b)=-f(b)

(23)

利用(22)、(23)式及换元可得

f(xy)=f(x)f(y)

(24)

由(20)、(23)、(24)式可得f是非零乘法奇函数。

定理2.3f是T3(F)保持逆矩阵的函数的充要条件是f=f-1(1)δ， 其中δ是域F上的满足δ(1)=1单的自同态。

证明首先证明充分性

∵δ是域F上的满足δ(1)=1单的自同态

=0

下面证明必要性。

再由Af及f的定义可知

通过矩阵的运算及f的定义可得

f(0)=0

(25)

(26)

(27)

(28)

利用(26)、(27)式及换元可以得到

f(1)f(xy)=f(x)f(y)

(29)

利用(26)、(28)、(29)式及换元可以得到

f(a+b)=f(a)+f(b)

(30)

利用类似定理2.1的证明可得f=f-1(1)δ， 其中δ是域F上的满足δ(1)=1单的自同态。