一类一阶迭代微分方程周期解的存在性1

黄明辉，赵国瑞

（广州城建职业学院 数学教研室，广东 广州 510925）

在迭代微分方程理论和应用领域中，解的存在性和唯一性是非常重要的问题.至今研究迭代微分方程有效的方法还是不动点理论[1-5].长期以来，迭代微分方程解的研究也得到了很多重要成果[5-8].

2010年， Berinde和Vasile[9]利用不动点理论研究了形如

一阶迭代微分方程解的存在性，其初始条件为 x ( t0) = x0.

2014年，Zhang[10]利用Schauder不动点定理研究了形如

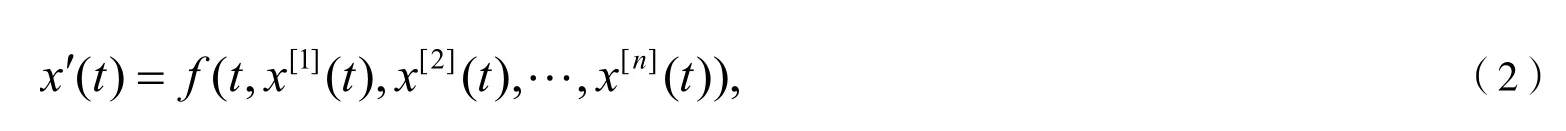
本文考虑利用Krasnoselskii不动点定理如下一类一阶迭代微分方程

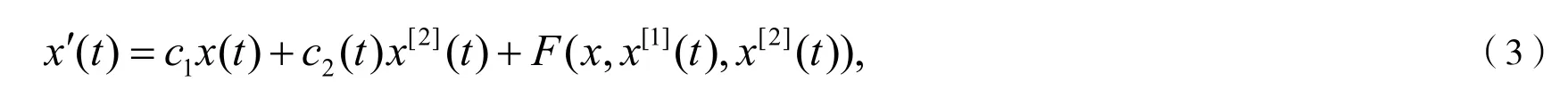
1 主要结论

定理1[11]设M 是Banach空间的一个有界凸非空子集.假设映射A、B将M映射到M，若

（ⅰ）对所有x，yM∈，有AxByM+∈，

（ⅱ）A是连续的和AM包含在M的一个紧子集上，

（ⅲ）B是压缩映射，

为了应用定理1，需要定义Banach空间的一个有界凸非空子集和两个映射：一个是全连续和一个是压缩映射.对于 P , L ≥ 0 ，定义集合

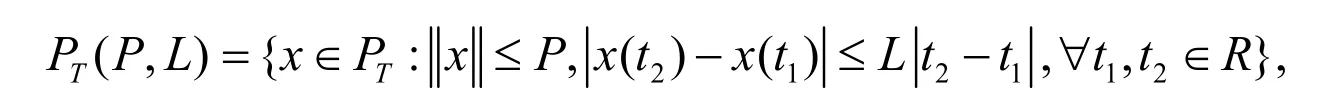
引理1[1]假设则

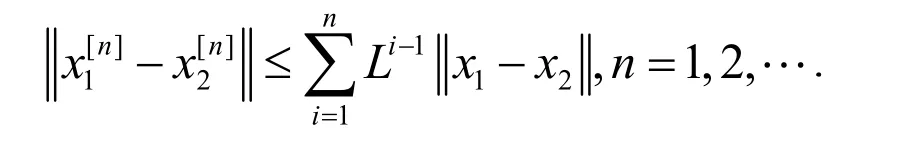
引理2假设10c≠ ，是方程（3）的解当且仅当

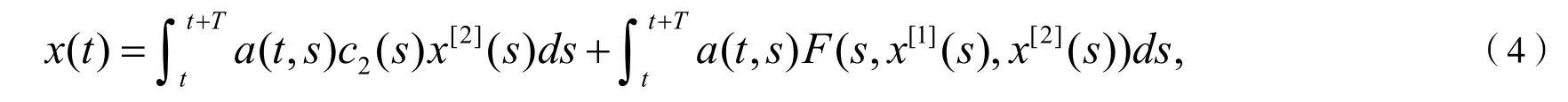
证明方程（3）两边同时乘以并从t到t T+ 积分，得

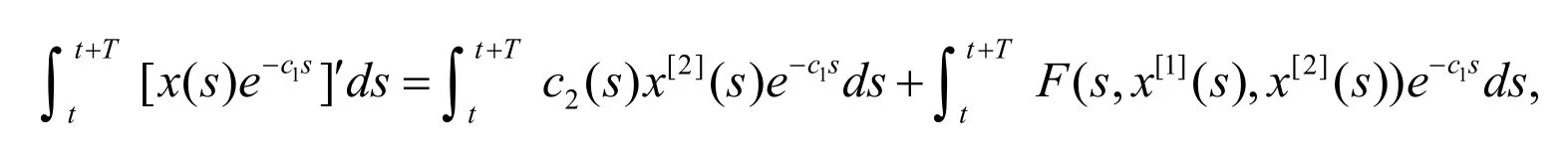
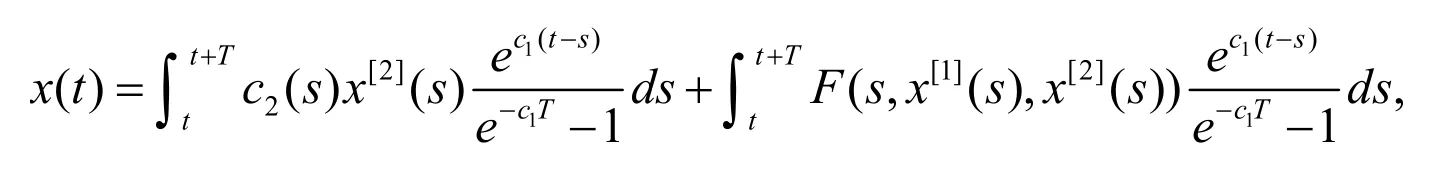
以上每一步都是可逆的.证明完成.

为了给出本文主要结果，假设以下条件成立：

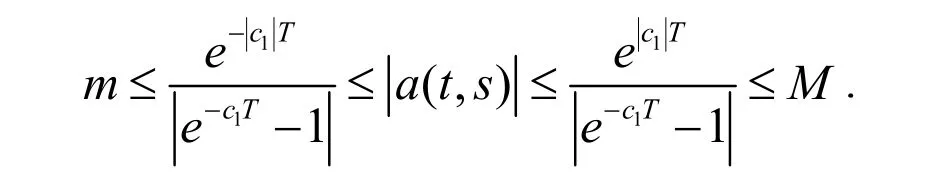
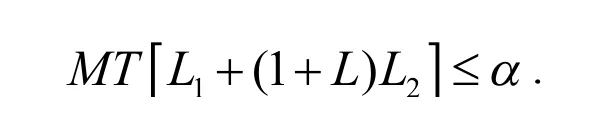
定义映射H

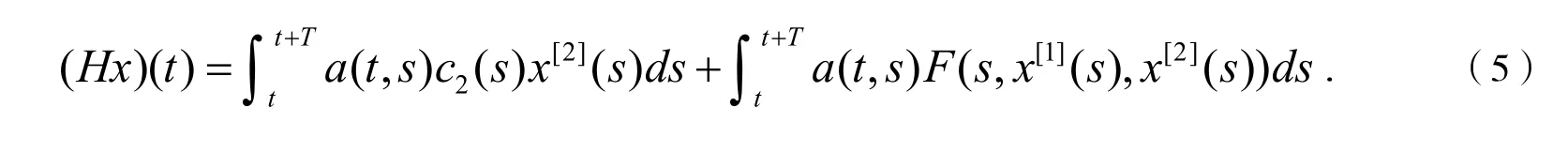
由引理2可知映射H的不动点是方程（3）的解，反之亦然.为了利用定理1，设映射如下

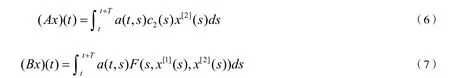
引理3假设（H1）-（H4）成立，则是全连续.

证明首先证是全连续.显然，若，故Ax是周期为T的周期函数.接着，证明A是连续的.设使得当时，.由Dominated Convergence 定理[11]可得，

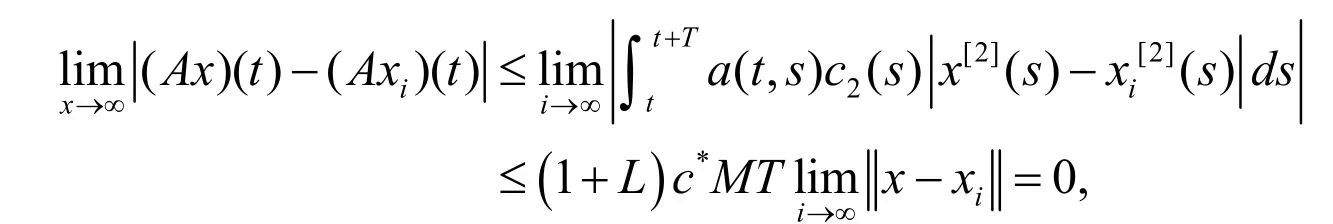
由Dominated Convergence定理可得，当.故Ax是等度连续的.由ArzelaAscoli定理可得，A是全连续的.

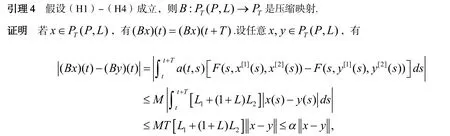
定理2假设条件（H1）-（H4）成立，且

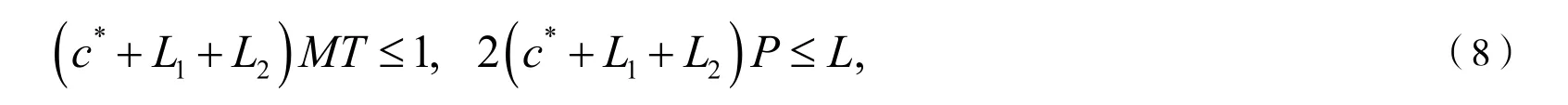
成立，则方程（3）在 PT( P, L)上至少存在一个周期为T的周期解.

证明若（H1）-（H4）成立，则引理2-4成立.由引理3可得，A是连续的和AM 包含在M 的一个紧子集上.同样，由引理4可知，则B是压缩映射.任意设x，

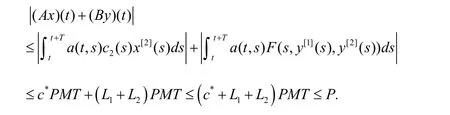
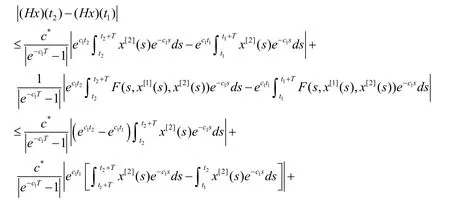
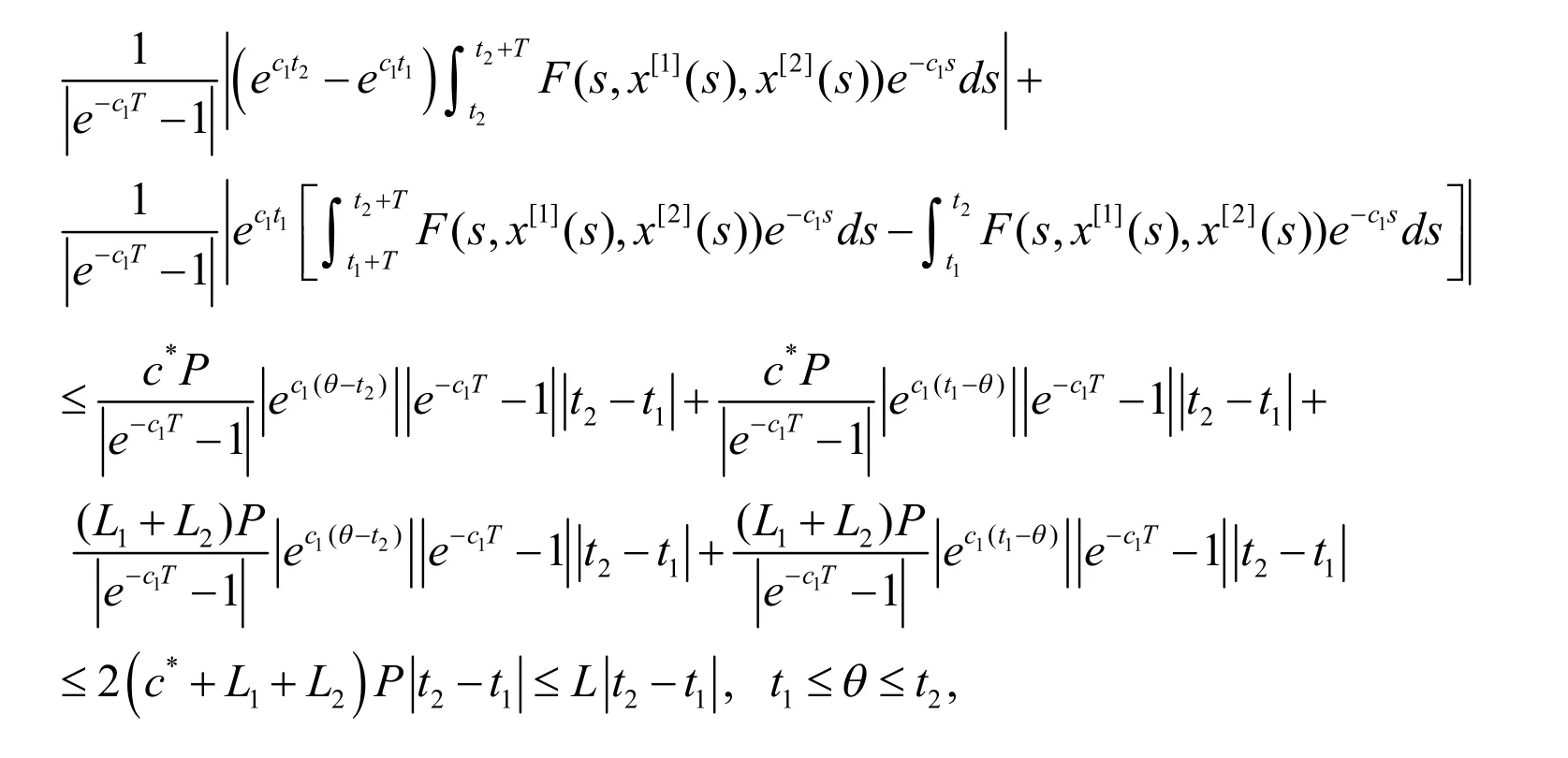
定理3除了定理1的假设之外，假设

证明设任意，有

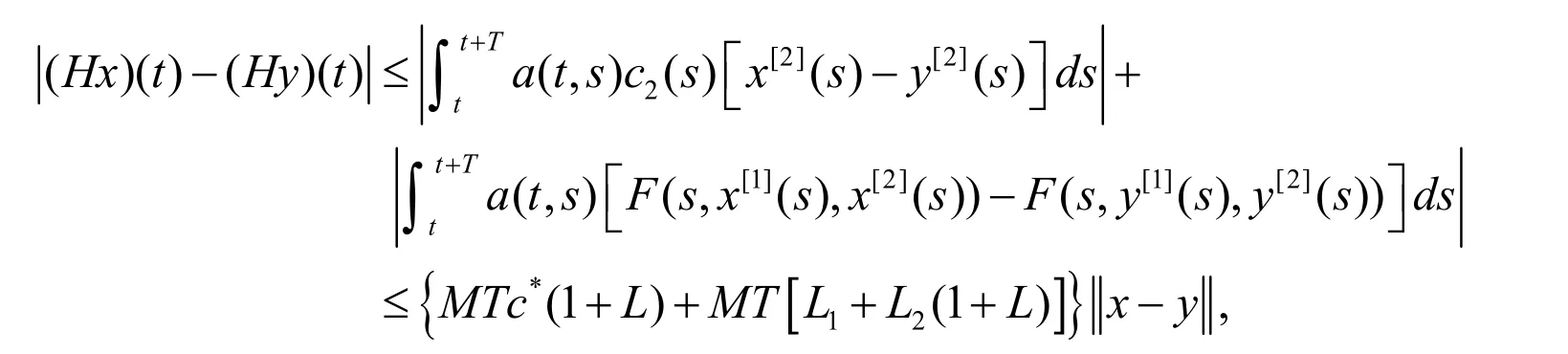
2 实例