DIRECT优化算法计算机仿真研究1

安华萍，李文静

（1.河源职业技术学院 电子与信息工程学院，广东 河源 517000；2.许昌学院 机电工程学院，河南 许昌 461000）

细分矩形方法（DIviding RECTangles，DIRECT）作为一种全局优化算法，由Donald R.Jones在1993年提出，它可以收敛并搜索到全局最佳点［1］.DIRECT算法将定义域当作一个维超矩形，并对其进行不断细分，然后根据每次迭代采样点函数估值和细分情况决定搜索区域，直至搜索到全局最优解，因此非常适合于黑箱函数的优化仿真.

然而，DIRECT算法需在定义域内多次采样才能保证搜索到全局最优解，其函数估值次数要比其它方法大的多，因此仿真过程需要消耗昂贵的计算机资源.如果能利用搜索过程中产生的采样点来构建精确的代理模型以替代复杂的源模型进行优化，那么就能大大减少源模型的迭代仿真次数，缩短优化时间，提高算法收敛速度，从而节省宝贵的计算机资源.基于此，本文提出一种新的DIRECT算法，通过对优化迭代过程中产生采样点的数据分析，构建比较精确的元模型，从而达到提高收敛速度的目的.

1 DIRECT算法

DIRECT方法是针对Lipschitz算法的不足而提出的，Lipschitz算法由于在搜索时必须取较大的常数而导致收敛速度缓慢.对于一个定义域为区间的函数（见图1），若搜索函数全局最小值，Lipschitz方法是假设存在一Lipschitz常数（此假设适用任意端点可估值闭区间），满足式：

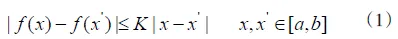
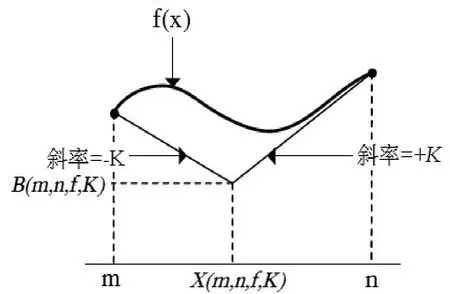
图1 计算Lipschitz下限值示意图

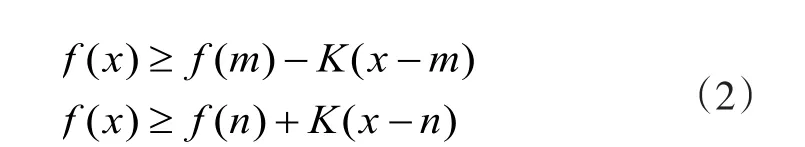
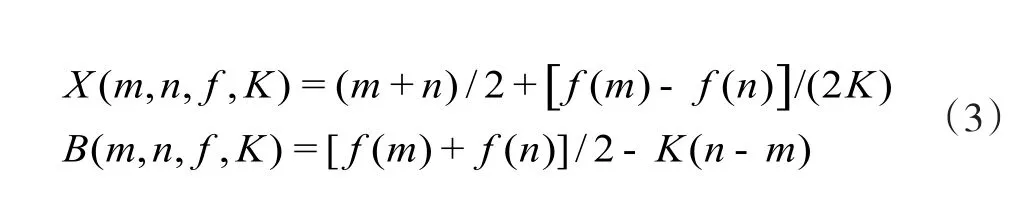
式（3）作为Lipschitz算法的核心要素，其算法步骤首先从函数端点和搜索，然后估算x1=X( a, b, f, K)函数值，因此将设计空间分为，然后选择拥有最小值的区间进行下一步搜索，估算值，此时将设计空间分为三个区间，依次类推，每次迭代过程中的采样点均在分段近似函数最小值位置，因而可以不断逼近函数，直至满足终止标准.这种算法的缺陷在于：（1）Lipschitz算法强调全局搜索，从而导致收敛速度缓慢；（2）在初始化过程中对函数端点和估算，尤其是扩展到维时需估算搜索空间的个顶点，因而进行优化过程中算法较复杂.

为了克服Lipschitz算法缺点，文献［1］通过改进设计空间的分割方法提出DIRECT算法.它着重强调对中心点而不是搜索空间的个顶点进行函数估值，用中心点区间，令式（1）中参数值为，则应满足式：

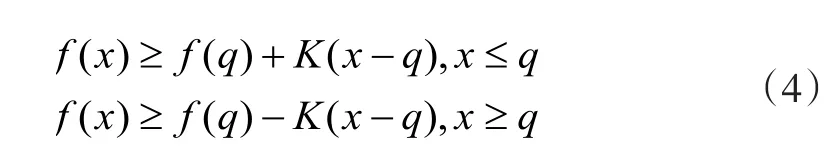
可以看出，其值只与区间中心点函数值有关.DIRECT算法则把迭代过程采样方式变为中心点采样，并对所有潜在优化区域进行采样，其算法步骤为：

对于多变量优化问题，则需要把一维DIRECT算法扩展至多维，这样搜索空间则转化为维超立方体单元，在搜索过程中，搜索空间被细分为更小的超立方体单元，因此，扩展过程中需要解决的关键问题：（1）如何细分这些超立方体.文献［2］指出可以任意选择一维将超立方体均分，其采样方式为围绕中心点上下左右进行，空心点为新的采样点；（2）如何使每个子超立方体单元均能在中心被采样，其详细步骤见文献［3］.DIRECT算法首先在同一维度上识别潜在最佳域.文献［4］指出将一超立方体细分为个超立方体单元，设 为第个单元中心点，为中心点与顶点之间距离，若有得超立方体满足

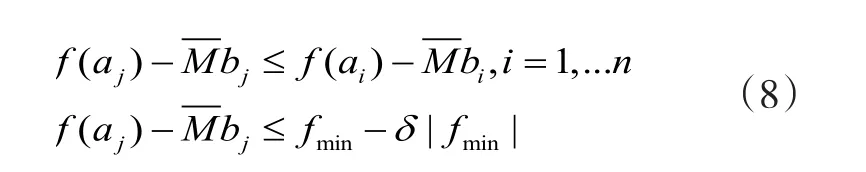
则称其为潜在最佳超立方体.

多维DIRECT具体算法步骤为

③按文献［2］所述方法细分超立方体，从超立方体处采样并对超立方体进行更小的子超立方体细分.更新为新采样点个数；

但是，在设计域内DIRECT算法需要多次采样，才能保证搜索到全局最佳点，特别是优化后期，采样点会越来越多，而且这些点为无效点，这样造成收敛速度愈加缓慢.况且在实际优化中，目标模型一般较复杂，这样优化算法往往很难被接受.

实际上，在最佳点域内，DIRECT算法假设目标函数是连续的，所以，可以利用最佳点域内的采样点来构造精确的近似模型，这样，即可加快算法收敛速度.元模型作为代理模型（Surrogate），利用最小二乘回归技术来实现二阶多项式模型的拟合，可以通过实验产生的采样点来构造与源模型相近的数学模型代替源模型进行仿真优化分析，因而能节约计算资源，降低计算量.

2 基于元模型的DIRECT算法

2.1 识别最优域

直接使用DIRECT算法产生的样本点构造元模型显然是不合适的，因为设计域内大量采样点会导致元模型径向基函数系数矩阵过于庞大.另外，采样点分布不均也不利于构造精确的模型.通过仿真分析可知，采样点一般聚集在局部最佳点附近.因此，要构造理想的元模型，就必须识别出包含当前最佳点的最优域.定义超立方体区域密度

①根据式（9）求整个定义域内平均域密度 ，找出函数值最小的当前采样点，即为当前最佳点；

②求最佳点与非最佳点之间的欧氏距离，对非最佳点集进行排序；从集合当前位置算出点的坐标值，计算其与前一点间的扩展区域；

2.2 基于元模型的DIRECT算法

在DIRECT算法中，利用当前采样点来构造精确的元模型，从而加快收敛速度，其具体步骤为

①按照原DIRECT算法进行采样；

②按式（8）识别潜在最佳超立方体，其中心点即为采样点，对该中心点进行函数估值；

③按2.1识别最优域；

④收集最优域内采样点，构建元模型；

⑤利用相关函数搜索最佳点，并进行函数估值，若该值小于所有采样点的函数值，则该值为当前最优值；

⑥判断是否收敛，若不满足转向步（2），否则退出循环.收敛条件为：当前最优值与预设值的绝对或相对误差小于（为设定极小值），或三次迭代最优值之差小于，或超出预设估算值次数.其流程图见图2.

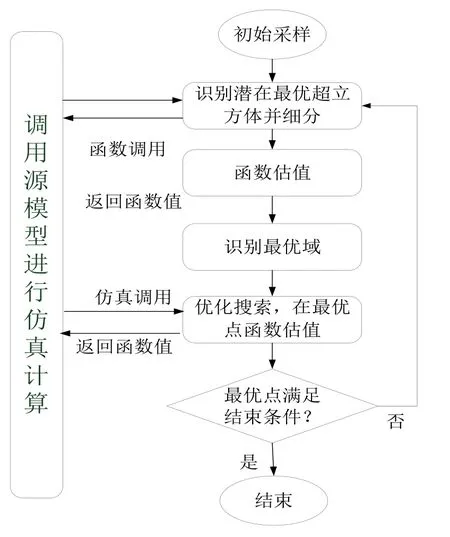
图2 基于元模型的DIRECT算法

3 数值分析

3.1 布兰（Branin）函数

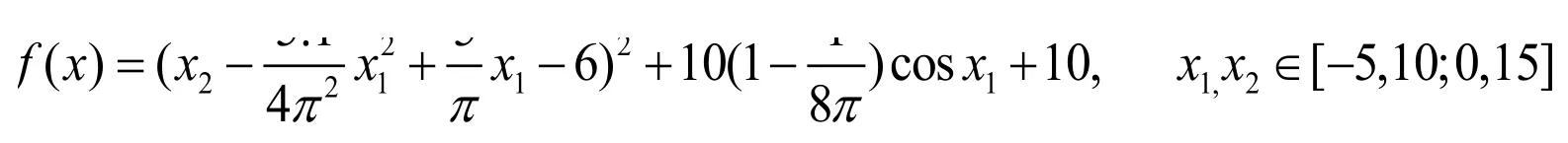
对比结果见表1，其中，orig表示原DIRECT算法，PRS［5］、RBF［6］、SVR［7］、KRIG［8］、MARS［8］表示基于不同元模型的DIRECT算法.

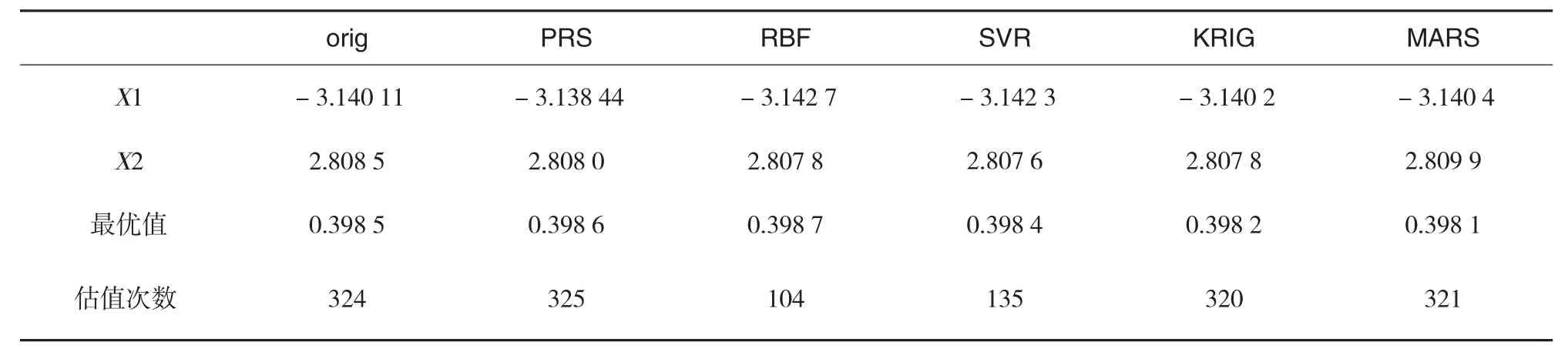
表1 布兰函数优化结果对比

3.2 六驼峰（six-hump camel-back）函数

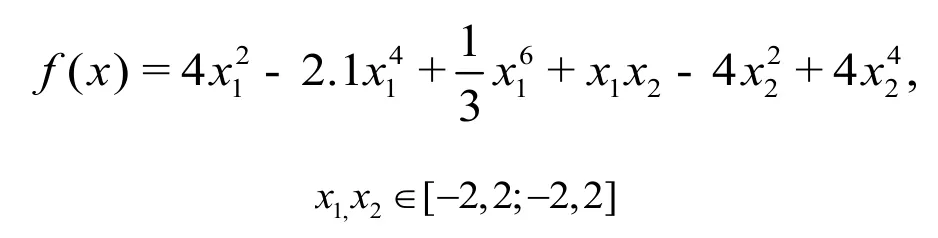
改进前DIRECT与改进后的DIRECT迭代优化对比结果见表2所示.其中，orig表示改进前DIRECT算法，PRS、RBF、SVR、KRIG、MARS表示基于不同元模型的改进DIRECT算法.

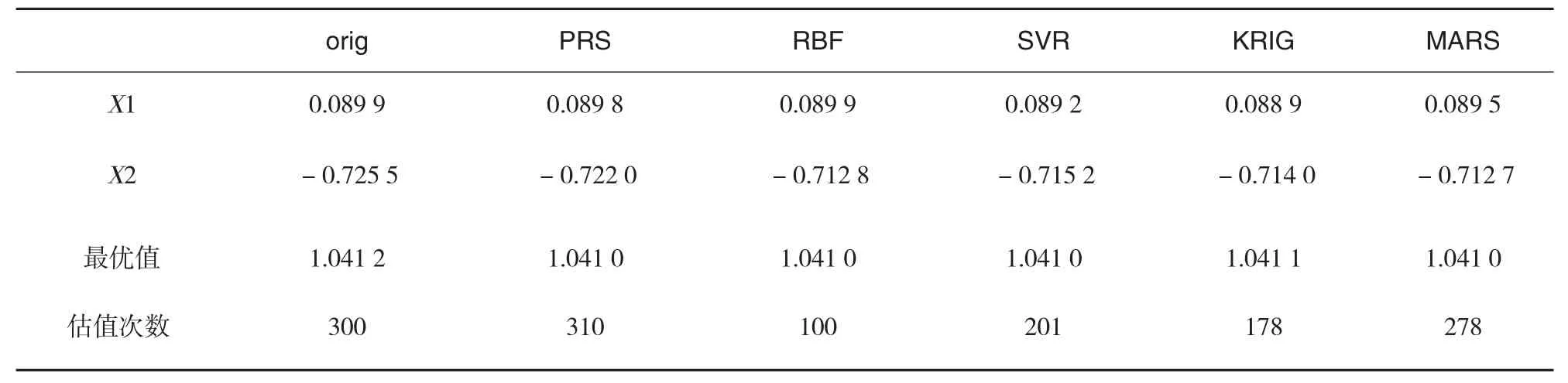
表2 六驼峰函数优化结果对比

从表1、表2可知，相比标准DIRECT算法，基于元模型的改进DIRECT算法更能快速地搜索至全局最优点，尤其是基于RBF元模型的DIRECT算法至少比原DIRECT算法减少三分之二，效果非常明显，这对于节约计算机资源，提高仿真优化效率具有重要意义.

4 结语

DIRECT算法由于函数估值次数多，所以会造成收敛速度缓慢，耗费较多的计算机资源，文章利用采样点来构造元模型，并搜索最佳点，从而加快该算法的收敛速度.通过上述函数及工程实例分析测试，表明该算法科学合理，效果良好，可以说，这是一种值得考虑并具有很大研究前景的方法，对于优化设计具有很重要的研究价值.