反结构混沌系统及其电路设计

颜闽秀, 徐 辉

(沈阳化工大学 a. 信息工程学院,b. 工业环境-资源协同控制与优化技术辽宁省高校重点实验室, 辽宁 沈阳 110142)

Lorenz系统[1]是于1963年首次被提出的混沌系统, Lorenz系统的提出, 翻开了混沌领域研究的篇章, 促进了混沌理论的发展和应用. 之后, 不同类型的混沌系统不断地被发现, 如Chen系统、 Lü系统、 Liu系统等[2-5], 而超混沌、 分数阶、 高维、 多翼混沌也相继被提出[6-8]. 在1983年, 蔡少棠提出了双涡卷电路且首次搭建非线性电路将其实现, 使其双涡卷电路模型成为研究混沌电路的经典模型. 因模拟电路能够有效地检测连续混沌系统的混沌特性, 所以被广泛应用于混沌系统的验证. 国内学者[9-12]对混沌系统的电路设计进行了深入研究, 并且详细阐述了混沌电路原理. 为了更深入地探索混沌系统的工程应用, 丰富混沌系统数量, 寻找新的混沌系统十分必要.

本文提出了4个新型四维混沌系统,它们互为反结构.关于反结构混沌系统,刘崇新首次于文献[13]中提到Liu系统[4]的反结构系统,并对其动力学特性进行了深入分析.

1 反结构系统模型及其一般特性分析

1.1 反结构系统总模型

本文提出的4个互为反结构的混沌系统总模型为式(1), 且每个系统均只含有一个非线性项.

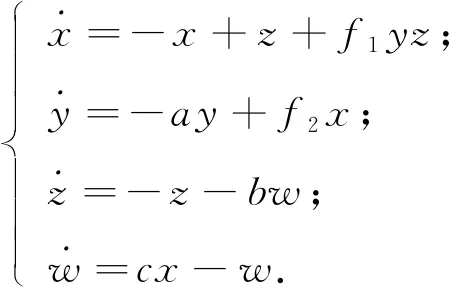
(1)

式中,系统固定的参数a=4,b=5,c=10,f1,f2为系统的反结构参数.式(1)的4个互为反结构的混沌系统为A、B、C、D.

A模型:f1=-1,f2=-1;

B模型:f1=1,f2=-1;

C模型:f1=1,f2=1;

D模型:f1=-1,f2=1.

给定初始值(1,1,1,1),绘制系统A、B、C、D的吸引子,如图1所示.可以看出系统B,C,D吸引子形状基本与系统A一致,但由于反结构参数的变化,使得吸引子的位置方向发生上下左右偏置.

1.2 系统的耗散性及其吸引子的存在性

从式(1)可以看出系统的耗散性与反结构参数f1,f2无关,所以互为反结构的4个系统A、B、C、D的耗散性一致.

(3)

式(3)表明当t趋向于无穷时,包含系统轨迹的每个体积元均以指数1+a+1+1 收缩到零,这说明了系统A、B、C、D吸引子的存在性.

图1 系统A、B、C、D的吸引子Fig.1 Attractors of system A, B, C and D

1.3系统的李雅普诺夫指数和维数

通过计算机分别求得系统A、B、C、D的李雅普诺夫指数λL1,λL2,λL3,λL4,根据式(4)求得系统A、B、C、D的李雅普诺夫维数DL.

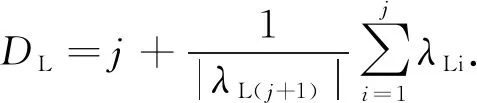
(4)

式中:i=1,2,3,4;j为满足式(5)的最大整数.

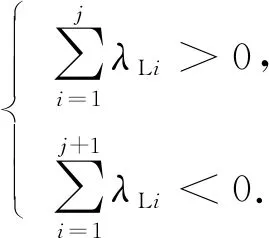
(5)

数据如表1所示.

表1 系统A、B、C、D的李雅普诺夫指数和维数Table 1 Lyapunov index and dimension of systems A, B, C and D

由表1能够看出, 系统A～D的李雅普诺夫指数λL均趋近于0, 所以4个系统均只有一个正的李雅普诺夫指数, 又因它们的李雅普诺夫维数是分数, 故判断出系统A、 B、 C、 D均为混沌系统.

1.4 系统的平衡点及其稳定性

计算出A、B、C、D的平衡点,并对在平衡点处线性化得到的Jacobian矩阵求取特征值,判断平衡点的稳定性.将所求的平衡点、特征值及判断出的稳定性绘制成表2.

表2 系统A、B、C、D的平衡点及其稳定性Table 2 Equilibrium point and its stability of systems A, B, C and D

由表2可知,混沌系统A、B、C、D都有2个平衡点,且都是不稳定的鞍点.

1.5 系统的分岔图和李雅普诺夫指数谱

下面以混沌系统A为例,分析其分岔图和李雅普诺夫指数谱.

固定参数b、c,令a∈[4,6],系统关于a的分岔图和李雅普诺夫指数谱如图2、图3所示.

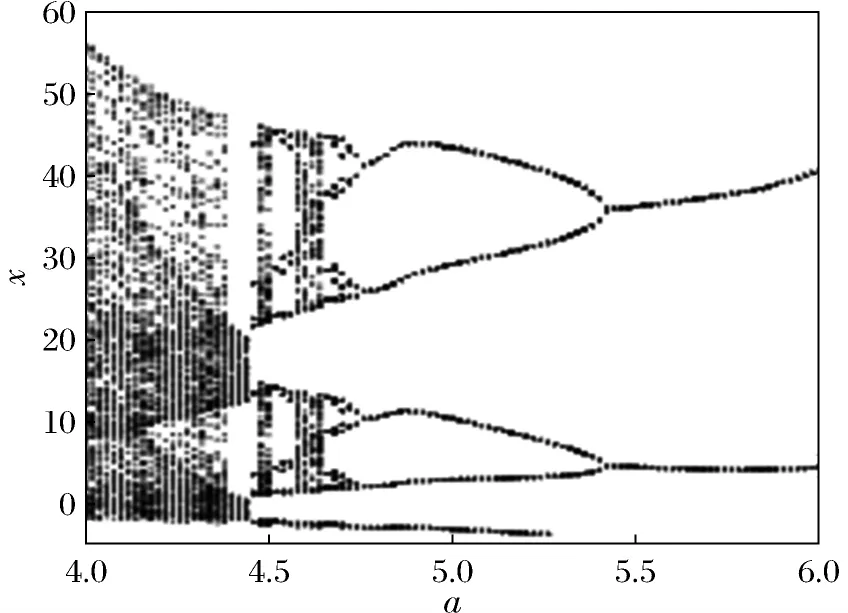
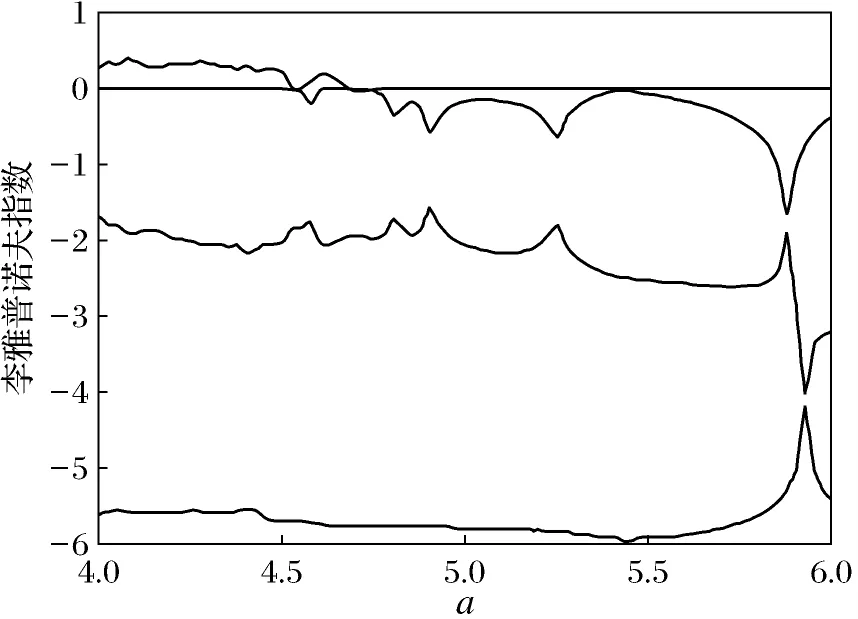
图2 系统A关于a的分岔图Fig.2 Bifurcation diagram of system A on a

当最大李雅普洛夫指数大于零时,系统处于混沌状态,会形成分岔图中的混沌区域.

从图2、图3中可以看出在区间[4.0,4.5]上时,系统最大的李雅普诺夫指数大于0,系统处于混沌状态.当a在区间(4.50,4.55]上 时,最大的李雅普诺夫指数小于或等于0,系统处于周期状态,分岔图中出现部分空白区域.当a在区间(4.55,4.67]上 时,最大的李雅普诺夫指数大于0,系统进入混沌状态,分岔图中出现由密集点构成的混沌区域.当a在区间(4.67,6.00]上时,最大的李雅普诺夫指数等于0,系统处于周期状态,分岔图中仅有部分点构成的曲线.

当固定参数a、c, 令b∈[0,5], 系统的分岔图如图4所示, 李雅普诺夫指数谱图如图5所示.

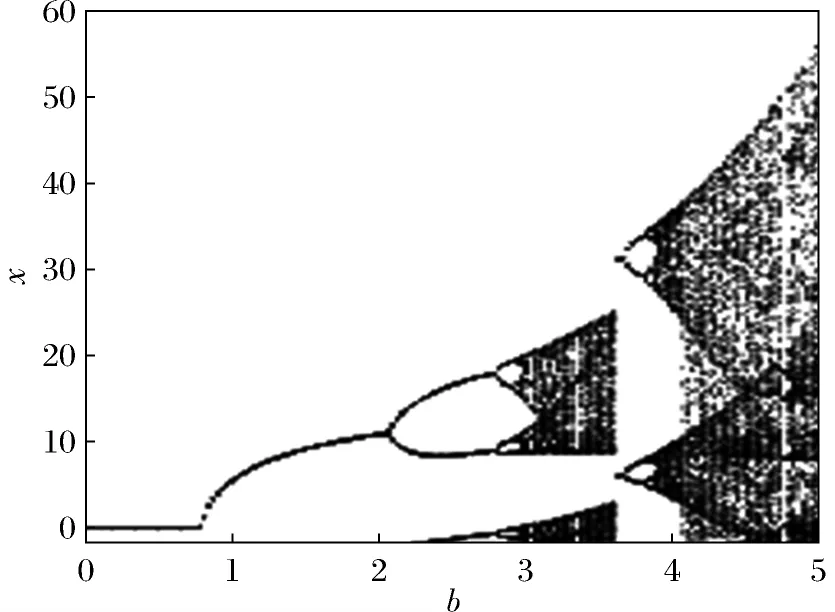
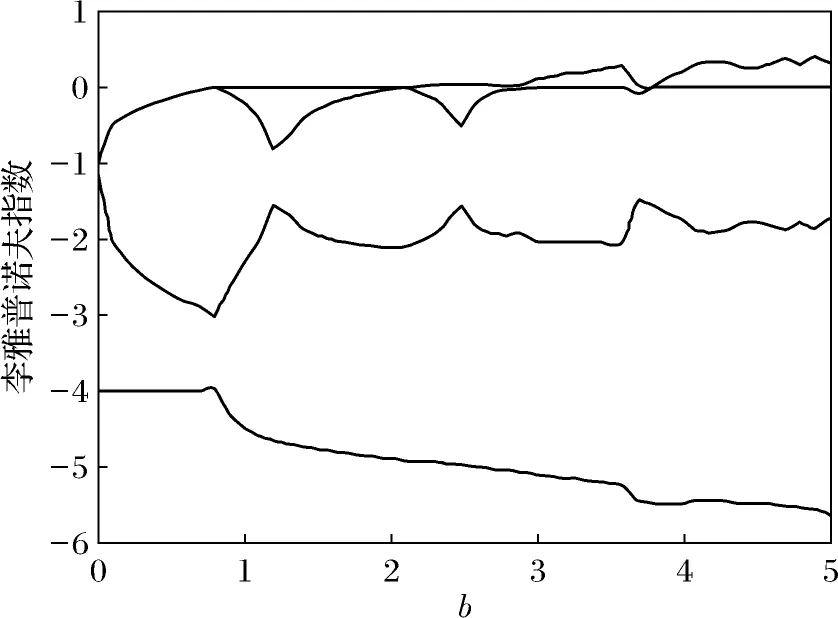
图4 系统A关于b的分岔图Fig.4 Bifurcation diagram of system A on b

由图4、图5可以看出, 在区间[0,2.9]时, 系统处于周期状态.在区间(2.9,3.7]上时, 系统由周期状态进入混沌状态, 分岔图在这区间上出现由密集点构成的区域. 在区间(3.7,3.8]上时, 最大的李雅普诺夫指数等于0, 系统处于周期状态, 导致分岔图中的分岔. 在区间(3.8,5.0]上时, 最大的李雅普诺夫指数大于0, 系统处于混沌状态.

当固定参数a、b,令c∈[0,10],也可以看出系统随参数变化时所具有的丰富混沌特性,这里不再赘述.

1.6 系统的功率谱和庞加莱截面

系统的动力学特性还可以通过观察系统的功率谱图和庞加莱截面图得到.

从图6、图7再次说明系统A、B、C、D是混沌的.

2 系统的电路设计与仿真实现

利用Multisim软件设计混沌电路进行模拟来判断本文提出的混沌系统能否物理实现,并对上述理论分析和仿真结果进行验证,Multisim设计实现该电路的原理图如图8所示.

图6 系统A、B、C、D的功率谱Fig.6 Power spectrum of systems A, B, C and D

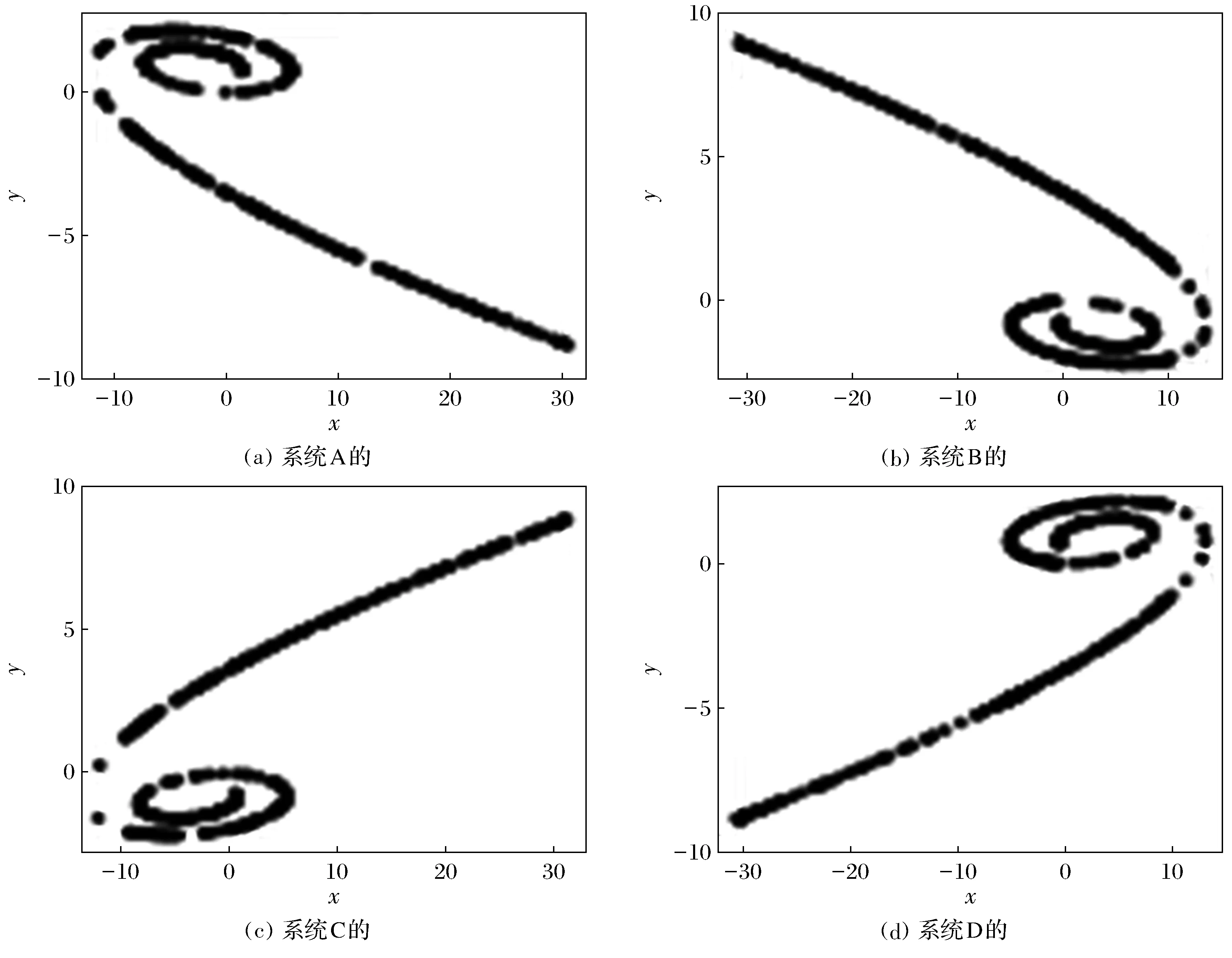
图7 系统A、B、C、D的庞加莱截面Fig.7 Poincare sections of systems A, B, C and D

图8 系统A的电路图Fig.8 Circuit diagram of system A

根据电路原理和电路理论得到混沌电路的实现方程为

(6)

将式(6)与系统A模型比较,可得:

(7)

在式(7)作为约束条件下,取值如式(8)

(8)

u1-u2相图表明了混沌系统A是可以以电路实现的,如图9所示.

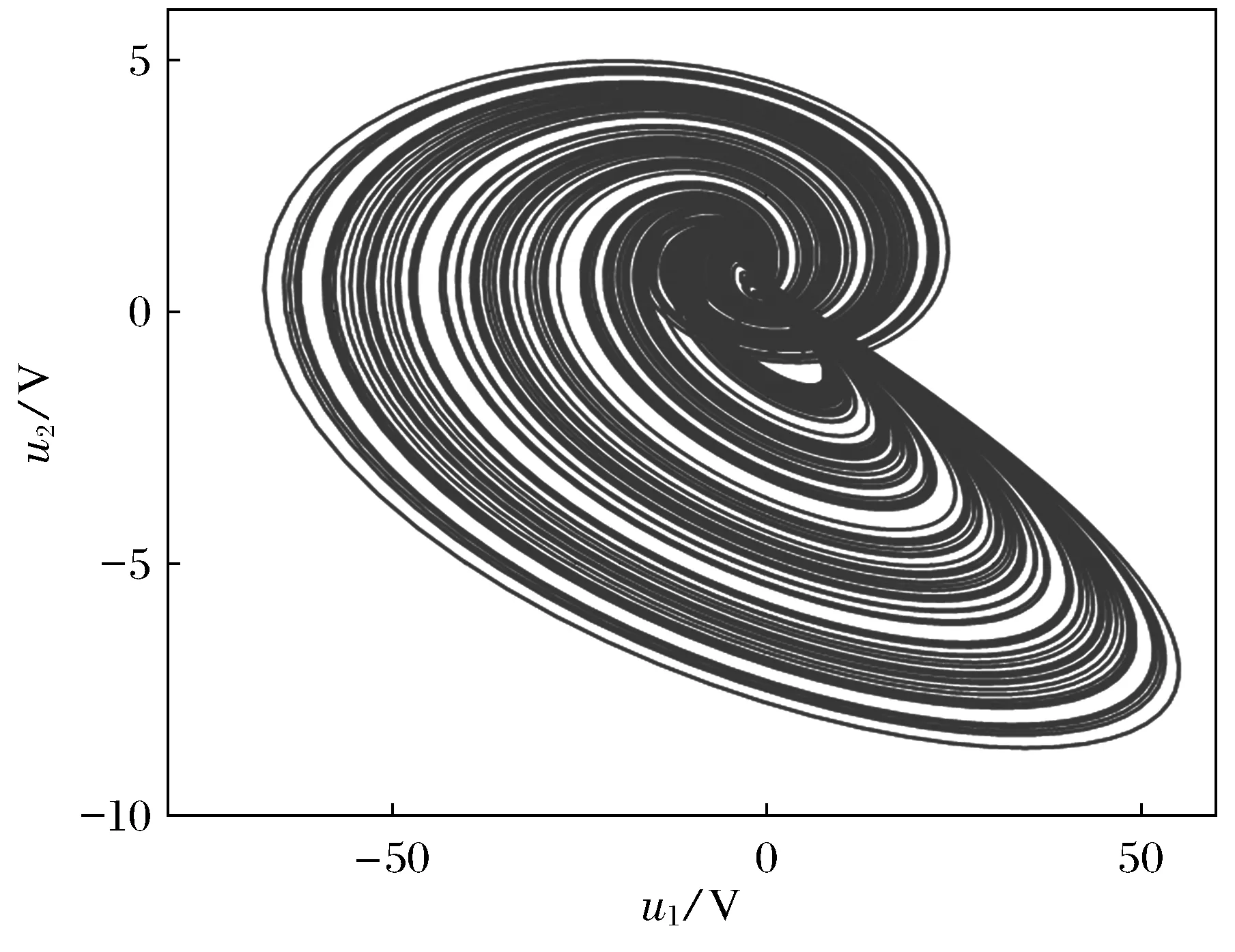
图9 u1-u2相图Fig.9 The phase trajectory of u1-u2

3 结 论

本文提出了4个新的仅含一个非线性项、互为反结构的混沌系统,为切换混沌系统的设计提供了可用的子系统,具有一定的研究意义,今后的工作就是以这4个子系统设计切实可行的新型切换混沌系统.