基于OIC的热轧轴压方矩形钢管局部屈曲承载力

熊 虎, 熊钰豪, 刘加景

(长安大学 建筑工程学院, 陕西 西安 710061)

近年来,空心截面钢材的应用日益增多.虽然空心型钢的价格比开口型钢高很多,但对称的外观以及良好的力学性能使空心型钢优势显著,不仅美观,而且结构质量轻,建造成本低.随着钢材强度的不断提高,钢材趋于薄柔,使得截面的局部失稳成为设计者关注的重点.

目前对热轧方矩形钢管(SHS/RHS)的局部屈曲问题,国外规范大都采用截面分类概念.如欧洲规范Eurocode 3根据板件宽厚比把截面分为Ⅳ类,第Ⅰ、Ⅱ类截面采用塑性设计,第Ⅲ类截面采用弹性设计,对于第Ⅳ类截面采用有效宽度法[1].人为地把截面进行分类使得第Ⅱ和第Ⅲ类截面的设计不连续,出现断层,这就给设计带来麻烦.不仅如此,随着钢材强度的提高,更多截面处于第Ⅳ类截面,而有效宽度法的烦琐计算使得设计变得困难.对于我国《钢结构设计标准》(GB 50017—2017),在考虑轴压下方矩形钢管的局部屈曲问题时以构件截面的平均应力达到钢材的屈服应力fy为极限状态,且宽厚比的限值是借用了箱型梁翼缘板的宽厚比限值结果[2],事实上二者不可能完全吻合.针对以上问题,本文采用有限元软件ABAQUS对轴压下热轧方矩形钢管局部屈曲承载力进行研究,根据数值结果拟合基于OIC(overall interaction concept)方法的公式.最后将公式计算结果与欧洲规范、我国标准和有限元计算结果进行对比分析.

1 有限元分析

1.1 试验构件概况

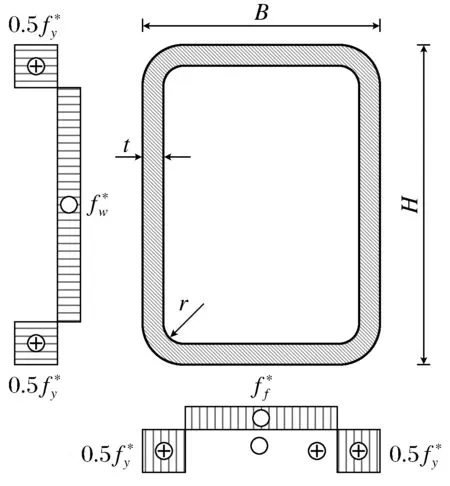
图1 方矩形截面形式及简化残余应力分布

1.2 有限元建模

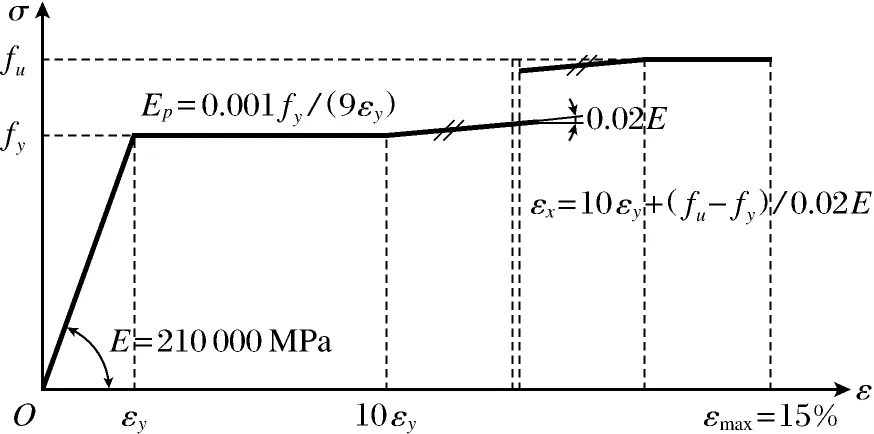
采用S4R单元模拟热轧方矩形钢管,文献[4-5]已经证明4结点四边形有限薄膜应变线性减缩积分壳单元(S4R单元)可以很理想地模拟构件真实状态,并能很好地进行线性特征值屈曲分析以及非线性大变形分析.在进行有限元模型的验证时本构关系应取试验构件的实测值,对于其他用于参数分析缺少材料性质数据的模型可按欧洲钢结构设计规范EN1993-1-1[1]建议的热轧构件本构关系输入,见图2.

为了使数值模型更为接近热轧方矩形钢管的真实工况,初始几何缺陷采用特征值屈曲分析所得的低阶模态,因为其能反映轴压构件最不利的几何缺陷模态,采用欧洲钢结构设计规范EN1993-1-5所建议的初始几何缺陷幅值200/h0,其中h0为方矩形截面腹板和翼缘净宽的较大值[6].图3是轴压下方矩形截面的低阶模态图.对于残余应力,按图1给出的简化残余应力输入模型.对于模型的边界条件应与试验模拟的实际边界条件吻合,即将构件两端结点分别刚性约束在2个参考点上,载荷作用在参考点上,允许载荷方向上的位移约束其他方向的位移.

恰当的网格划分是模型计算效率和计算精确度的保证, 本文采用文献[5]已经验证的网格密度, 即横向截面网格单元长度取翼缘和腹板较大净宽的1/20, 对于纵向构件长度方向网格单元长度取构件长度的1/50, 结果表明网格如此划分既能保证计算结果的精确度又能兼顾计算的效率.

1.3 有限元结果与试验结果对比

本文对收集的8个轴压方矩形试验[7]进行了数值模拟,以验证用于参数分析的有限元模型的可靠性,试验构件的基本参数及试验与有限元计算的极限承载力对比见表1.表中试验编号形式为RHS(SHS)_S355(钢材强度)_HR(热轧)_H×B×t,短柱试验构件的长度取截面最大尺寸的3倍.目的是为了避免整体失稳.FExp、FFEM分别表示试验与有限元得出的极限承载力,由表可知,试验结果与有限元结果十分接近,证明有限元所建模型与构件实际状态是符合的.图4、图5分别给出试验与模型的破坏形态对比图及试验与模型得出的载荷-位移曲线对比图,从图中可以看出,试验结果与有限元模型结果都十分接近.

表1 试验与有限元模拟结果对比Table 1 Comparison of experimental and finite element results

综上所述,建立的有限元模型可以准确地模拟构件真实状态,可用于轴压下热轧方矩形钢管局部屈曲承载力参数研究.

1.4 参数分析

利用经验证的有限元模型对轴压下的热轧方矩形钢管局部屈曲进行参数分析,得出建议的OIC公式.研究参数包括钢材强度、截面高宽比、板件宽厚比,其中钢材强度包括S235、S355、S460,截面高宽比H/B为1.0、1.5、2.0、2.5,板件宽厚比范围为15～115,取值间隔为2,共612个有限元模型.所建模型截面角圆弧的内径r与截面厚度t相等.

图4 RHS 250×150×5.0试验与有限元屈曲模态对比

图5 RHS 250×150×5.0试验与有限元载荷-位移曲线对比

2 OIC方法

OIC方法的提出是基于Aryton-Perry公式,2013年Boissonnade[8]首先提出OIC方法,它同现今广泛应用的连续强度法(CSM)、直接强度法(DSM)一样都是基于计算机辅助的一种设计方法.CSM的提出是基于应变形式,用于厚实截面;DSM是基于Winter有限宽度法的形式用于薄柔截面.OIC基于Aryton-Perry公式在合适位置插入参数得到改进的公式不仅可以用与局部屈曲问题,还能处理整体失稳问题,相较于其他方法OIC不仅理论完善,且应用简便,这也是本文选择OIC方法的原因.

2.1 改进的Aryton-Perry公式

经典的Aryton-Perry公式是基于压杆稳定考虑初弯曲得来的,见式(1),

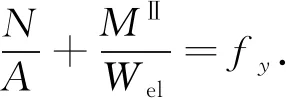
(1)

式中:N为轴力;A为截面面积;MⅡ表示跨中截面所受弯矩;Wel为截面弹性模量,fy是屈服应力.

(2)

式中:σult=N/A;v0为初位移幅值,σcr为构件临界应力.式(2)进一步整理得式(3),

(σcr-σult)(fy-σult)=σultσcrη.

(3)

式中,η为缺陷影响因子,η=v0A/Wel.

式(3)两边同时除以fy,并以χ和λ的形式表示得:

(1-χ)(1-χλ2)=ηχ.

(4)

式中:χ为折减因子;λ为相对长细比.

为了更为准确地考虑缺陷影响,Dwight[9]提出建议公式

η=α(λ-λ0).

(5)

式中:α为缺陷因子;0为进入塑性的临界值[10].

式(4)针对的是整体失稳,对于构件的截面行为有类似的表示,如式(6),

(1-χcs)(1-χcsλcs)=ηcsχcs.

(6)

式中:χcs为截面折减因子;λcs为截面相对长细比;ηcs为截面缺陷影响因子.

OIC中对于局部屈曲考虑应变强化、残余应力、初始缺陷及屈曲后强度影响因素,在式(6)合适位置插入参数得:

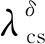
(7)

式中:ηcs=αcs(λcs-λ0);β是厚实截面应变强化对局部屈曲承载力的影响因子;αcs是中间类型截面缺陷因子;δ是薄柔截面屈曲后强度的影响因子.

可通过图6来理解β、αcs、δ、λ04个参数,当λ∈[0,λ0]时构件处于应变影响区,即应变强化是构件的承载力极限,当λ∈[λ0,1]时构件处于缺陷影响最大的初始缺陷区域,当λ≥1时构件处于失稳区,即构件的承载极限由失稳状态决定.

对式(7)进一步变换可得:

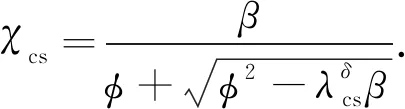
(8)

式中φ=0.5(1+αcs(λcs-λ0)+λδβ).本文的目的就是利用经验证的有限元模型,拟合得出4个参数的值,得到χcs与λcs关系曲线,即OIC相互作用设计曲线,最终得到轴压下热轧方矩形钢管局部屈曲承载力设计新方法,并将计算结果与欧洲规范和我国钢结构标准进行对比.

①、②、③—构件处于理想状态,即αcs=0时的承载力极限状态;④、⑤、⑥—构件处于理想状态,即αcs=0时的稳定极限状态;⑦—构件真实情况.

2.2 OIC方法应用步骤

OIC方法的关键在于设计曲线,见图7.OIC方法的应用步骤如下[10-11].

①、②—理想状态下的设计曲线; ③—构件真实状态的设计曲线.

1) 计算承载力极限Rpl;

2) 使用有限条软件CUFSM计算稳定极限Rcr;

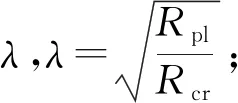
4) 由图7的设计曲线,通过步骤3计算所得的λ计算χ值,χ=f0(λ);

5) 计算构件真实的承载力极限Rb=χRpl.

3 有限元计算结果分析

对612个有限元模型进行了分析计算,图8给出的是按S235,S355, S460三类钢材等级划分的全部计算结果,从图8可以得出,随着钢材等级的提高,χcs值变大,但是差别并不大,最大差值仅为4%,故接下来的参数研究只取钢材等级为S235的钢构件进行分析.

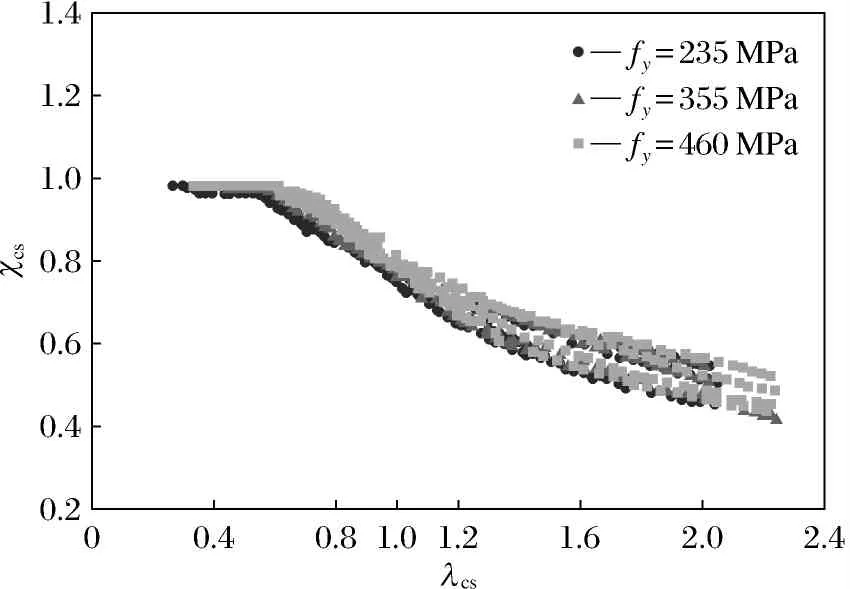
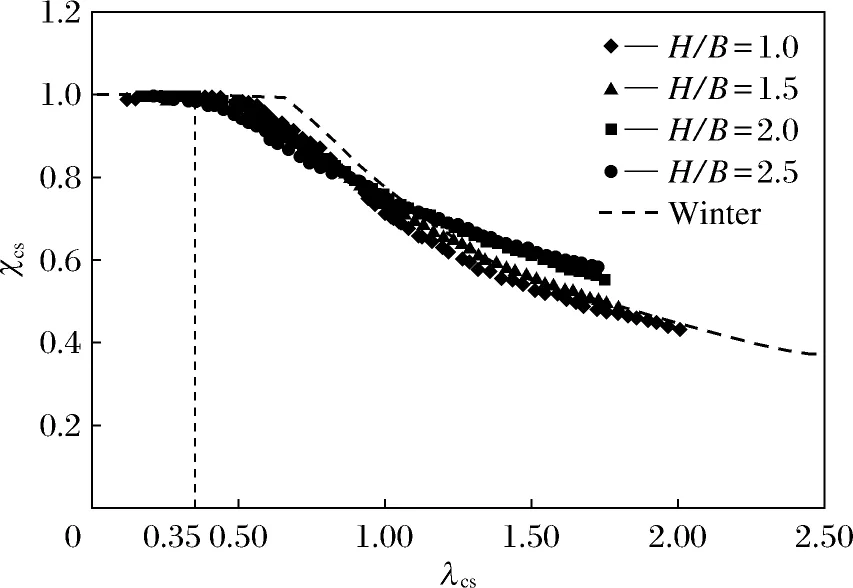
图9给出了轴压下热轧方矩形钢管局部屈曲关于截面高宽比H/B的数值结果.本文研究的是等厚热轧方矩形钢管,故H/B是影响其局部屈曲承载力的关键所在.如图9所示,在λcs<0.35时,截面属于厚实截面,截面高宽比的不同对于截面极限承载的影响并不大,在0.35≤λcs≤1.00时,截面处于初始缺陷影响明显的半厚实截面,截面宽厚比越大,极限承载力越小,这主要是因为此类截面缺陷敏感度很大,截面高宽比越大缺陷越大,所以截面极限承载力越低;当λcs>1.00时,截面属于薄柔截面,失稳是极限承载力的主要因素.截面高宽比越大,截面极限承载力越大.这是因为当截面为方形时(H/B=1)组成截面的板件是同时屈曲的,而矩形截面(H/B>1)组成截面的较宽板件先屈曲,而较窄的板件对其有嵌固作用,使屈曲后的板件产生了“薄膜拉力”,进而应力重分布,使得极限承载力提高,这就是屈曲后强度,OIC公式中参数δ是影响其值的关键.越薄柔的板件,产生的“薄膜拉力”越大.对屈曲的板件嵌固作用越大,从而提高了极限承载力.

根据有限元结果对OIC公式中4个参数β、αcs、δ、0分析如下.

1) 由图9可知,在λcs>1.00的失稳区,有效宽度法中Winter公式明显不符合有限元结果的趋势,因此根据有限元结果,通过最佳拟合提出δ关于高厚比的线性函数,

δ=-0.4H/B+1.45,(1≤H/B≤2.5).

3) 根据图9的观察结果,λ0取0.35,因为当λ0≤0.35时,χcs=1.0,它是截面按塑性设计的最大截面相对长细比.

4) 0.35≤λcs≤1.00是缺陷影响区,关于该区域放大图见图10,通过局部拟合σcs的值取0.15.轴压下热轧方矩形钢管局部屈曲的建议OIC设计曲线见图11.

图10 图9区域放大图Fig.10 Zoomed area of Fig.9

图11 轴压下热轧方矩形钢管局部屈曲的建议OIC设计曲线

4 OIC建议公式计算结果与欧洲规范和我国标准对比

4.1 OIC建议公式与欧洲规范对比

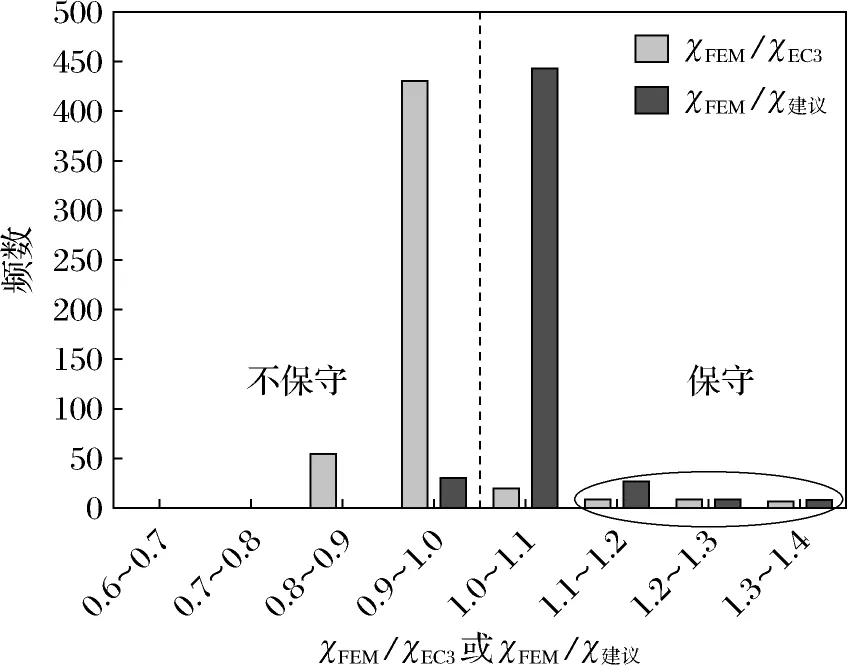
图12是有限元与欧洲规范的比值(χFEM/χEC3)及有限元与建议公式的比值(χFEM/χ建议)与相对长细比λcs的关系图,图13是图12的更好阐述,通过对频数的统计,可直观地看出不同方法对比的结果.

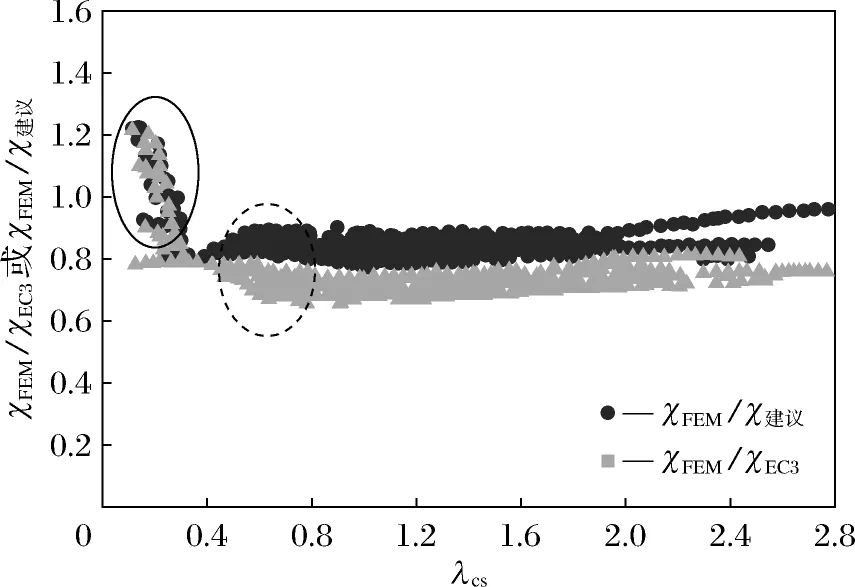
由图12、图13分析可得:

1) 在截面相对长细比较小的实线圈中,欧洲规范与建议公式结果重合且比值均大于1,因为热轧构件应变硬化发生大变形情形,这使得构件不能正常使用,故建议公式与欧洲规范均没有利用应变强化;

2) 在虚线圈中欧洲规范较建议公式存在明显的不连续性,这是因为欧洲规范采用的“截面分类法”的第Ⅲ类(弹性设计),与第Ⅳ类(有效宽度法设计)截面设计方法不同;

3) 总体来看欧洲规范设计方法较建议方法偏于不保守,容易造成设计上的错误.

4.2 OIC建议公式与我国标准建议公式对比

图14、图15是有限元、我国标准、建议公式所得χcs值的比较,与建议公式与欧洲规范对比类同.

由图14、图15分析可得:

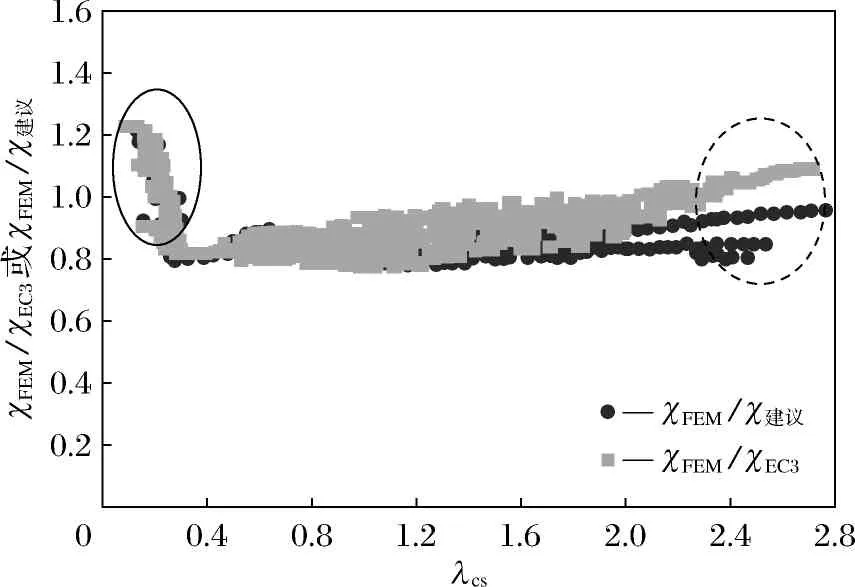
图14 热轧轴压方矩形截面有限元、我国规范、建议公式所得χcs值的比较

Fig.14 Comparisons of χcs values obtained by FEM, GB and suggested formulas for square and rectangular cross section of hot rolling under axial compression

1) 在截面相对长细比较小的实线圈中,我国标准与建议公式结果重合且比值均大于1,因为热轧构件应变硬化发生大变形情形,这使得构件不能正常使用,故建议公式与我国标准均没有利用应变强化;

2) 总体来说, 我国标准设计方法较建议设计方法更为保守, 尤其在相对长细比较大时更为突出;

表2是欧洲规范、我国标准及建议公式与有限元计算结果对比的数值分析结果.我国规范与有限元结果差别最大,建议公式最为接近.

表2 欧洲规范、我国标准、建议公式与有限元计算结果对比

5 结 语

本文对轴压下热轧方矩形钢管局部屈曲承载力进行了研究,收集试验数据对建立的有限元模型进行验证.利用经验证的有限元模型对轴压热轧方矩形钢管局部屈曲承载力进行参数分析,进而得出建议的OIC设计公式,将我国标准设计方法、欧洲规范设计方法与建议的OIC方法进行对比分析.

1) 所建模型充分考虑了初始缺陷、残余应力对局部屈曲的影响,经验证能准确模拟构件的真实工况.

2) 经参数分析研究得出,钢材强度对轴压热轧方矩形钢管局部屈曲影响不大,截面高宽比H/B是主要影响因素.

3) 欧洲钢结构设计规范,我国标准及建议公式在截面相对长细比较小时,也即厚实截面情形,计算结果一致.均偏保守的不利用应变强化.其他截面类型欧洲规范普遍偏于不安全,尤其是在薄柔截面国标过于保守.相比之下,OIC建议设计方法与有限元结果最为接近,不仅应用简便,且结果更为精确,是一种简单高效的设计方法.