区间值序列与区间值函数列的收敛性
李改利,高 丽
(延安大学 数学与计算机科学学院,陕西 延安 716000)
区间数理论的基本思想是应用区间数变量代替点变量进行计算。早在1931年,Young给出了区间数的概念,区间数理论作为处理不确定性问题的理论基础之一,被广泛应用于工程技术和管理决策等诸多领域中。为了更好的处理一些实际问题,人们在区间值空间中引入了多种度量(距离)公式。我们拟定在区间值空间上的Hausdorff度量下讨论区间值序列与区间值函数列的收敛性问题[1-9]。
本文在介绍区间数及区间值空间的基本概念及其相关性质的基础上:1)引入了区间值序列的收敛性概念并给出其相关性质;2)引入了区间值函数列的收敛性概念并给出其相关性质。
1 预备知识
1.1 区间数的定义及区间值空间上的度量
定义1.1[1]设a,b∈R且a≤b,则称有界闭区间[a,b]为R上的一个区间数,R上全体区间数构成的集合称为区间值空间,记为[R]。当b≥a≥0时,称[a,b]为正区间数,其全体构成的集合称为正区间值空间,记[R+]为;当a≤b≤0时,称[a,b]为负区间数,其全体构成的集合称为负区间值空间,记为[R-]。

定义1.2[4]设z1=[a1,b1],z2=[a2,b2]∈[R],则称
dH(z1,z2)=max{|a1-a2|,|b1-b2|}
为区间数z1,z2的Hausdorff距离。
区间值空间[R]在Hausdorff距离之下成为完备的度量空间[9],并且具有下列性质:
dH(ka,kb)=|k|dH(a,b),k∈R,
dH(a,b)≤dH(a,c)+dH(c,b),

1.2 区间数的运算及大小关系
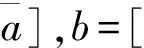
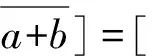


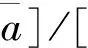


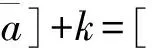
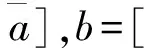
2 区间值序列的收敛性
定义2.1 设[a1,b1],[a2,b2],…,[an,bn]…是一列定义在同一个区间值空间[R]上的区间数,则称[a1,b1],[a2,b2],…,[an,bn]…为定义在区间值空间[R]上的区间值序列。记为{[an,bn]}⊂[R](n=1,2,…),且[a,b]∈[R]。
定义2.2[4]设区间值序列为{[an,bn]}⊂[R](n=1,2,…),且[a,b]∈[R],如果对任给的ε>0,存在自然数N,当n>N时,有
dH([an,bn],[a,b])<ε,

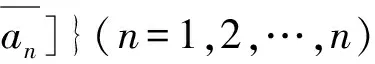



从而有

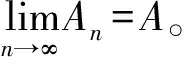


从而有

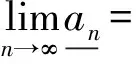
定理2.2[1]设[an,bn],[cn,dn]∈[R](n=1,2,…),
[a,b],[c,b]∈[R],k∈R,如果
则有
证明由于
因此只需要证明和、积与倒数的运算即可。

dH([[an,bn],[a,b])<ε,当n>N1;
dH([cn,dn],[c,d])<ε,当n>N2。
取N=max{N1,N2},则当n>N时,上述两个不等式同时成立,从而
dH([an,bn]+[cn,dn],[a,b]+[c,d])≤
dH([an,bn]+[cn,dn],[an,bn]+[c,d])+
dH([an,bn]+[c,d],[a,b]+[c,d])=
dH([cn,dn],[c,d])+dH([an,bn],[a,b])<
ε+ε=2ε,

设[an,bn]·[cn,dn]=[rn,sn][a,b]·
[c,d]=[r,s],其中
rn=min{ancn,andn,bncn,bndn},
sn=max{ancn,andn,bncn,bndn},
r=min{ac,ad,bc,bd},
s=max{ac,ad,bc,bd}。
从而
dH([an,bn]·[cn,dn],[a,b]·[c,d])=
max{|rn-r|,|sn-s|}。
若rn=ancn,r=bd,则rn≤bndn,r≤ac,从而
rn-r=ancn-bd≤bndn-bd,
rn-r=ancn-bd≥ancn-ac。
则由数列极限的四则运算及夹逼定理得
当rn与r为其他情况时,证明过程类似,从略。
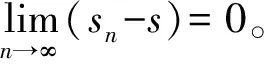
则对ε>0,当n>N时,有
dH([an,bn]·[cn,dn],[a,b]·[c,d])=
max{|rn-r|,|sn-s|}<ε,


由实数列极限的相关运算性质得
定理2.3 设[an,bn]∈[R](n=1,2,…),且[a,b],[c,d]∈[R],k∈R。若
则[a,b]=[c,d]。
证明因为
所以对任给的ε>0,分别存在N1,N2∈N,有
dH([an,bn],[a,b])=max{|an-a|,|bn-b|}<ε,
当n>N1;
dH([an,bn],[c,d])=max{|an-c|,|bn-d|}<ε,
当n>N2。
则|an-a|<ε,|bn-b|<ε,|an-c|<ε,|bn-d|<ε。
从而
|a-c|=|(an-a)-(an-c)|≤
|an-a|+|an-c|<
ε+ε=2ε,
|b-d|=|(bn-b)-(bn-d)|≤
|bn-b|+|bn-d|<
ε+ε=2ε。
取N=max{N1,N2},则当n>N时,上述两个不等式同时成立,从而有
dH([a,b],[c,d])=max{|a-c|,b-d}<
ε+ε=2ε,
即[a,b]=[c,d]。
定理2.4 设两个区间值序列{[an,bn]},{[cn,dn]}∈[R](n=1,2,…)都收敛,若存在N∈N+,使得当n>N时,有[an,bn]≤[cn,dn],则
证明设
则有
dH([an,bn],[a,b])<ε,
dH([cn,dn],[c,d])<ε,
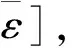
[a,b]-ε<[an,bn],当n>N1;
[cn,dn]<[c,d]+ε,当n>N2。
取N={N0,N1,N2},上述两个不等式成立,则当n>N时,有
[a,b]-ε<[an,bn]≤[cn,dn]<[c,d]+ε,
则有[a,b]<[c,d]+2ε。
由ε的任意性有[a,b]≤[c,d],
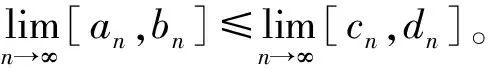
3 区间值函数列的收敛性
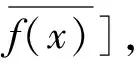
定义3.2 设f1(x),f2(x),…,fn(x),…是一列定义在同一个区间I上的区间值函数,则称f1(x),f2(x),…,fn(x),…为定义在区间I上的区间值函数列,记为{fn(x)}。
定义3.3 设{fn(x)}为区间I上的区间值函数列,且f(x)在I上有定义。若对x0∈I,有区间值序列f1(x0),f2(x0),…,fn(x0),…收敛,则称区间值函数列{fn(x)}在点x0处收敛,并称x0为区间值函数列的收敛点。如果区间值序列f1(x0),f2(x0),…,fn(x0),…发散,则称区间值函数列{fn(x)}在点x0处发散。如果区间值函数列{fn(x)}在区间I上的每一点都收敛,则称区间值函数列{fn(x)}在区间I上收敛。区间值函数列{fn(x)}所有收敛点组成的集合,称为区间值函数列{fn(x)}的收敛域。
定义3.4 设{fn(x)}和f(x)分别为定义在区间I上的区间值函数列和区间值函数,如果对任给的ε>0,存在N>0,当n>N时,对任意x∈I,有
dH(fn(x),f(x))<ε。
则称区间值函数列{fn(x)}在区间I上一致收敛于f(x)。
定理3.1 设{fn(x)}和{gn(x)}为定义在区间I上的两个区间值函数列,且k∈R,如果有



dH(fn(x),f(x))<ε,当n>N1;
dH(gn(x),g(x))<ε,当n>N2。
取N=max{N1,N2},当n>N时,上述两个不等式同时成立,从而有
dH(fn(x)+gn(x),f(x)+g(x))≤
dH(fn(x)+gn(x),fn(x)+g(x))+
dH(fn(x)+g(x),f(x)+g(x))=
dH(gn(x),g(x))+dH(fn(x),f(x))<
ε+ε=2ε。
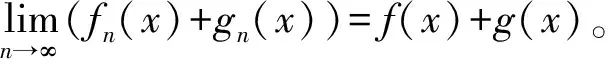
对ε>0,当n>N时,有
dH(fn(x)·gn(x),f(x)·g(x))≤
dH(fn(x)·gn(x),f(x)·gn(x))+
dH(f(x)·gn(x),f(x)·g(x))=
gn(x)·dH(fn(x),f(x))+f(x)·dH(gn(x),g(x))。
则可知dH(fn(x)·gn(x),f(x)·g(x))<ε,即
由实数列极限的相关运算性质得
定理3.2 设{fn(x)}为定义在区间I上的区间值函数列,f(x),g(x)为定义在区间I上的两个区间值函数,如果有
则有f(x)=g(x)。

dH(fn(x),f(x))=

当n>N1;
dH(fn(x),g(x))=

当n>N2。
从而有


所以
|f(x)-g(x)|=
|(fn(x)-f(x))-(fn(x)-g(x))|≤
|fn(x)-f(x)|+|fn(x)-g(x)|<2ε,

取N=max{N1,N2},当n>N时,上述两个式子同时成立,从而有
dH(f(x),g(x))=
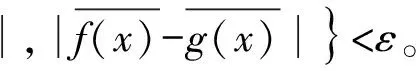
即f(x)=g(x)。
定理3.3 区间值函数列{fn(x)}在区间I上一致收敛的充分必要条件是:对任给的ε>0,存在N>0,当n,m>N时,对任意x∈I,有
dH(fn(x),fm(x))<ε。
证明必要性 设{fn(x)}在区间I上一致收敛于f(x),则由定义3.3,对任给的ε>0,存在N>0,当n>N时,对任给x∈I,有
所以当n,m>N时,有
dH(fn(x),fm(x))≤
dH(fn(x),f(x))+dH(fm(x),f(x))<
充分性 设对任给的ε>0,存在N>0,当n,m>N时,对任意x∈I,有
dH(fn(x),fm(x))=


即对任给的ε>0,存在N>0,当n>N时,对任意x∈I,有
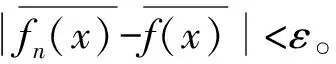
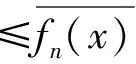
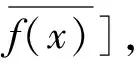
dH(fn(x),f(x))=

于是由定义3.3,区间值函数列{fn(x)}在I上一致收敛于区间值函数f(x)。
4 结束语
本文通过介绍区间数及区间值空间的基本概念及其相关性质,给出了区间值序列的收敛性及其有关性质,同时给出了区间值函数列的收敛、一致收敛性概念及其相关性质。这些研究结论对进一步研究区间值空间的分析性质具有一定的参考意义。

