新超混沌及其复混沌系统设计与电路实现

方 洁，姜明浩，李宗翰，刘 娜，邓 玮

(郑州轻工业大学 电气信息工程学院，河南 郑州 450002)

0 引 言

混沌是非线性动力学系统中存在一种特有的不可预测的、类似随机性的运动形式。超混沌系统具有两个或两个以上正的李雅普诺夫指数，具有复杂的动力学行为，超混沌系统构建和实现是混沌研究的一个重要方向，对深入理解混沌信号产生的本质以及工程实践具有重要理论价值和现实意义[1]。

在已有文献中，对混沌系统构建研究大多是在实数域上完成的。Fang等[2]基于超混沌系统特征，构建了新的四维超混沌系统，分析了动力学特性并搭建了仿真电路。Zhang等[3]提出了具有蝴蝶效应的超混沌系统，通过数值模拟和电路实现的方法，研究了系统的基本动力学性质。Rajagopal 等[4]构建了一个由四维超混沌系统改进而成的新型磁控四维混沌系统，并采用自适应滑模控制方法实现了系统的同步。Shikha等[5]构建了具有双涡旋吸引子的四维连续自治超混沌系统，通过理论分析和数值仿真研究系统基本动力学性质。Singh等[6]构造了3个具有二次平衡面的四维超混沌系统，该系统表现出3种超混沌态和5种混沌态。Chen等[7]提出了一个新的四维超混沌系统，该系统同时满足高复杂度、强鲁棒性和均匀分布带宽等重要性质。Yang等[8]通过将一个特定的三维混沌系统线性扩充为六维系统，研究了如何用隐藏吸引子来创建一个特定的超混沌系统的方法。Ma等[9]基于忆阻电容器构建了一个简单混沌电路，并在数字信号处理器平台上实现了该电路。马旭炯等[10]构造了一个四维离散超混沌系统，结合重复量化算法分析了其动力学特性。

复混沌系统中存在复变量，复变量经过虚实部分离后具有双倍的变量数，产生的混沌信号具有更加不可预测性和随机性，使得复混沌系统在保密通信领域有着巨大的应用潜力。目前关于复混沌系统研究已经取得了一系列进展。党红刚等[11]研究了一个三维混沌复系统的基本性质，实现了系统的自适应混沌同步和参数辨识。张芳芳等[12]研究了时滞复Lorenz系统的动态特性及时滞因数的影响，并基于非线性反馈控制方法实现了复Lorenz系统的自时滞混沌同步。Liu等[13]以超混沌复系统为载体，研究了该系统的动力学行为，通过将脉冲注入控制参数中来增强该混沌系统的随机性，并将其应用于彩色图像加密中。Sun等[14]构建了一个新的复混沌系统，分析了其动力学行为，实现了3个复混沌系统的组合函数投影同步。Huang等[15]在采样数据控制的基础上，通过将复混沌系统分解为2个实系统，研究了时滞复混沌Lur’e系统的主从同步问题。Liu等[16]基于自适应控制技术，实现了具有已知或未知复变量的复混沌系统的组合函数投影同步。Mahmoud等[17]通过设计自适应复滞后同步控制器，构建了一组具有未知参数的复混沌系统，实现了两个系统的滞后同步。Zhao等[18]采用主动控制方案，研究了复数域上激光混沌系统的复杂自同步。

在实数域与复数域混沌系统研究的基础上，基于产生超混沌系统需要满足的2个必要条件构建了一个新的四维超混沌系统。对该系统进行了理论推导和数值模拟，研究了该系统的基本动力学特性，并分析了参数改变时系统的动力学行为的变化，从多方面验证了该系统的混沌行为。并以该超混沌系统为基础，将系统变量从实数域扩展到复数域，得到了一个新的复混沌系统。该复混沌系统具有2个正的李雅普诺夫指数，能够产生丰富的动力学行为。运用Multisim软件对所设计的超混沌系统及其对应的复混沌系统进行电路仿真，电路仿真结果和数值分析结果吻合，表明了所设计新混沌系统的物理可实现性。

1 超混沌系统分析

构建超混沌系统必须满足2个必要条件：一是对于自治系统而言，至少是四维的；二是至少有2个正的李雅普诺夫指数且所有李雅普诺夫指数之和小于零。基于2个必要条件，构造四维超混沌系统如式(1)。

(1)

式中：a，b，c，d，r，e为实常数。当参数a=27，b=1.5，c=5，d=43，r=0.5，e=3.5时，系统存在一典型的超混沌吸引子，如图1所示。

2 新超混沌系统的基本动力学特性

2.1 耗散性和吸引子的存在性

通过式(1)所构造四维超混沌系统的梯度(能量函数)为

(2)

要想确保该系统是耗散的，必须满足-a-c-b+r<0。当a=27，b=1.5，c=5，d=43，r=0.5，e=3.5时，满足耗散性条件，即当t→∞时，系统的轨迹最终以指数速率渐近地收缩到一个特定的零体积的极限集中，并最终被固定在一个吸引子上。

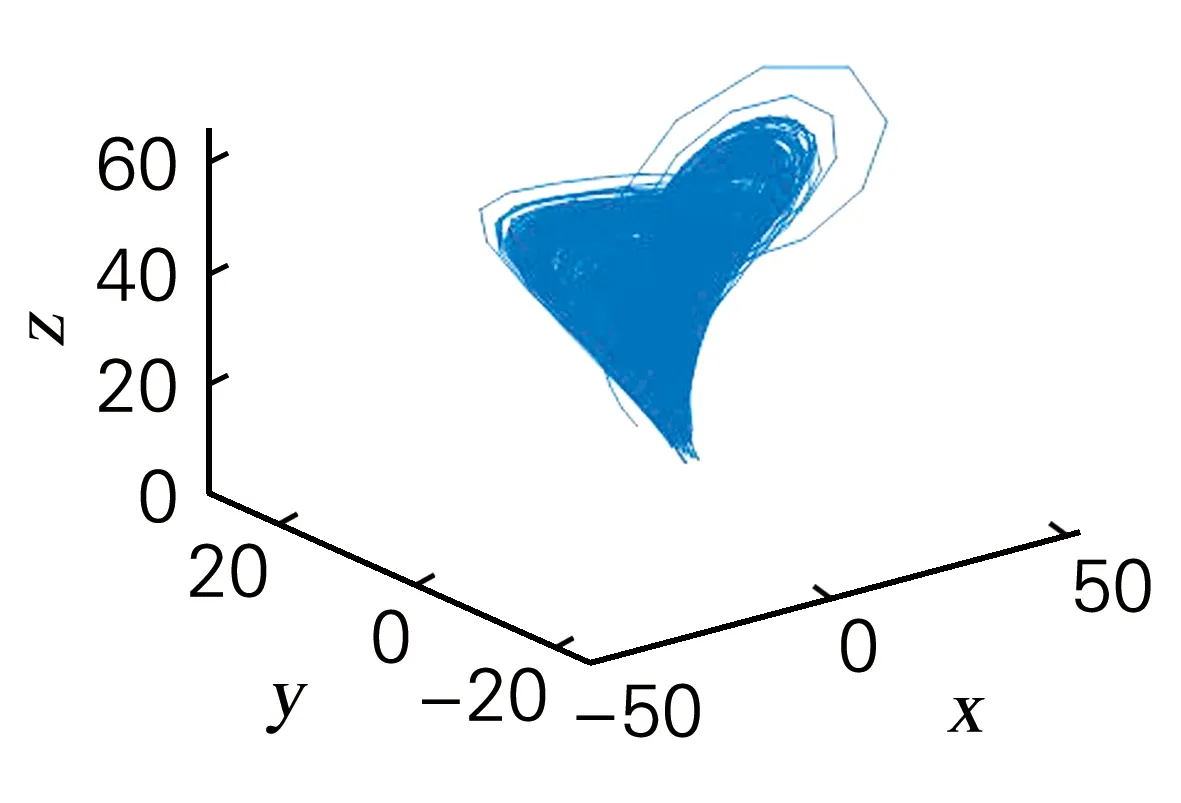
(a) x-y-z三维相图

2.2 平衡点及稳定性

令所构造系统的右边等于零，即

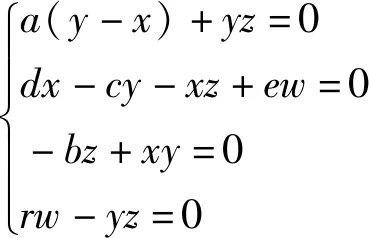
(3)

求解式(3)，可得系统3个平衡点：S0=(0，0，0，0)；S1=(-52.556 9，-5.990 3，209.883，-2 514.6)；S2=(52.556 9，5.990 3，209.883，2 514.6)。

在所构造系统的平衡点处，对系统进行线性化得其Jacobian矩阵为

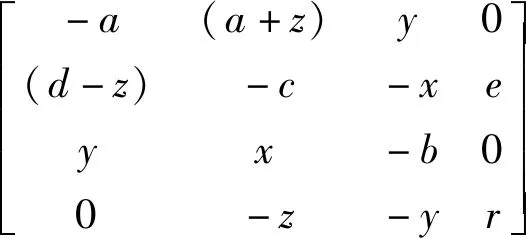
S0处计算可得4个特征根λ1=-51.805，λ2=19.805，λ3=1.5，λ4=0.5。λ1为负且λ2、λ3、λ4为正，S0为不稳定的鞍点。S1处计算可得4个特征根λ1=-13.455+206.92j，λ2=-13.455-206.92j，λ3=-6.339，λ4=0.248。λ3为负数，λ4为正数，λ1λ2为实部为负的共轭复数，S1为不稳定的鞍焦点。S2处计算可得4个特征根λ1=-13.429+206.919j，λ2=-13.429-206.919j，λ3=-6.288，λ4=3.147。λ3为负数，λ4为正数，λ1、λ2为实部为负的共轭复数，S2为不稳定的鞍焦点。

2.3 新混沌系统李雅普诺夫指数及李雅普诺夫维数

采用雅阁比矩阵方法计算系统的李雅普诺夫指数，得到LE1=0.458 349，LE2=0.181 250 9，LE3=0，LE4=-33.611 039，即该系统有2个正的李雅普诺夫指数，因此是超混沌的。新混沌系统李雅普诺夫指数如图2所示。

图2 新混沌系统李雅普诺夫指数图Fig.2 Lyapunov exponents spectrum of new chaotic system

新系统的李雅普诺夫维数为分数维，进一步说明新系统是混沌的。

2.4 参数变化对系统的影响

参数的改变，系统的稳定性会发生变化，使系统处于不同的状态。可用李雅普诺夫指数谱及分岔图对照分析系统状态变化。

固定参数b=1.5，c=5，d=43，r=0.5，e=3.5改变a，a∈(15，40)。系统的李雅普诺夫指数谱(第4条李雅普诺夫指数曲线省略)及分岔图如图3所示。当a∈(15，17.5)时系统处于超混沌、混沌、拟周期、周期交替出现状态；当a∈(17.5，21)时系统处于混沌状态；当a∈(21，22)系统处于拟周期状态；当a∈(22，24.2)系统处于周期状态；当a∈(24.2，26.6)时，系统处于超混沌、混沌、拟周期、周期交替出现状态；当a∈(26.6，30)系统处于超混沌状态；当a∈(30，33.3)时系统处于周期状态；当a∈(33.3，34.3)系统处于拟周期状态；当a∈(34.3，40)系统处于混沌状态。

(a) 李雅普诺夫指数谱

固定参数a=27，c=5，d=43，r=0.5，e=3.5 改变b，b∈(0，25)。系统的李雅普诺夫指数谱及分岔图如图4所示。当b∈(0，1)时，系统处于混沌、周期、拟周期交替出现状态。当b∈(1，4.4)时，系统处于超混沌状态；当b∈(4.4，5.25)系统处于周期状态；当b∈(5.25，7.05)时系统处于混沌状态；当b∈(7.05，8.78)时，系统处于周期状态；当b∈(8.78，12.6)时，系统处于混沌状态；当b∈(12.6，18.85)时，系统处于拟周期状态；当b∈(18.85，25)时，系统处于周期状态。

(a) 李雅普诺夫指数谱

固定参数a=27，b=1.5，d=43，r=0.5，e=3.5改变c，c∈(25，55)。系统的李雅普诺夫指数谱及分岔图如图5所示。当c∈(0，14)时，系统处于超混沌、混沌交替出现状态；当c∈(14，30)时系统处于周期状态。

固定参数a=27，b=1.5，c=5，r=0.5，e=3.5 改变d，d∈(25，55)。系统的李雅普诺夫指数谱及分岔图分别如图6所示。当d∈(25，26.9)时，系统处于拟周期状态；当d∈(26.9，29)时，系统处于混沌状态；当d∈(29，30.6)时，系统处于周期、混沌交替出现状态；当d∈(30.6，44)时，系统处于超混沌状态；当d∈(44，48.6)时，系统处于周期状态；当d∈(48.6，51.5)时，系统处于混沌状态；当d∈(51.5，55)时，系统处于周期状态。

固定参数a=27，b=1.5，c=5，d=43，e=3.5改变参数r，r∈(-20，3.5)。超混沌系统的李雅普诺夫指数谱及分岔图如图7所示。当r∈(-20，-17.2)时，系统处于周期状态；当r∈(-17.2，-7.4)时系统处于混沌状态；当r∈(-7.4，-1.5)时系统处于周期状态；当r∈(-1.5，1.6)时系统处于超混沌状态；当r∈(1.6，3.5)时系统处于混沌状态。

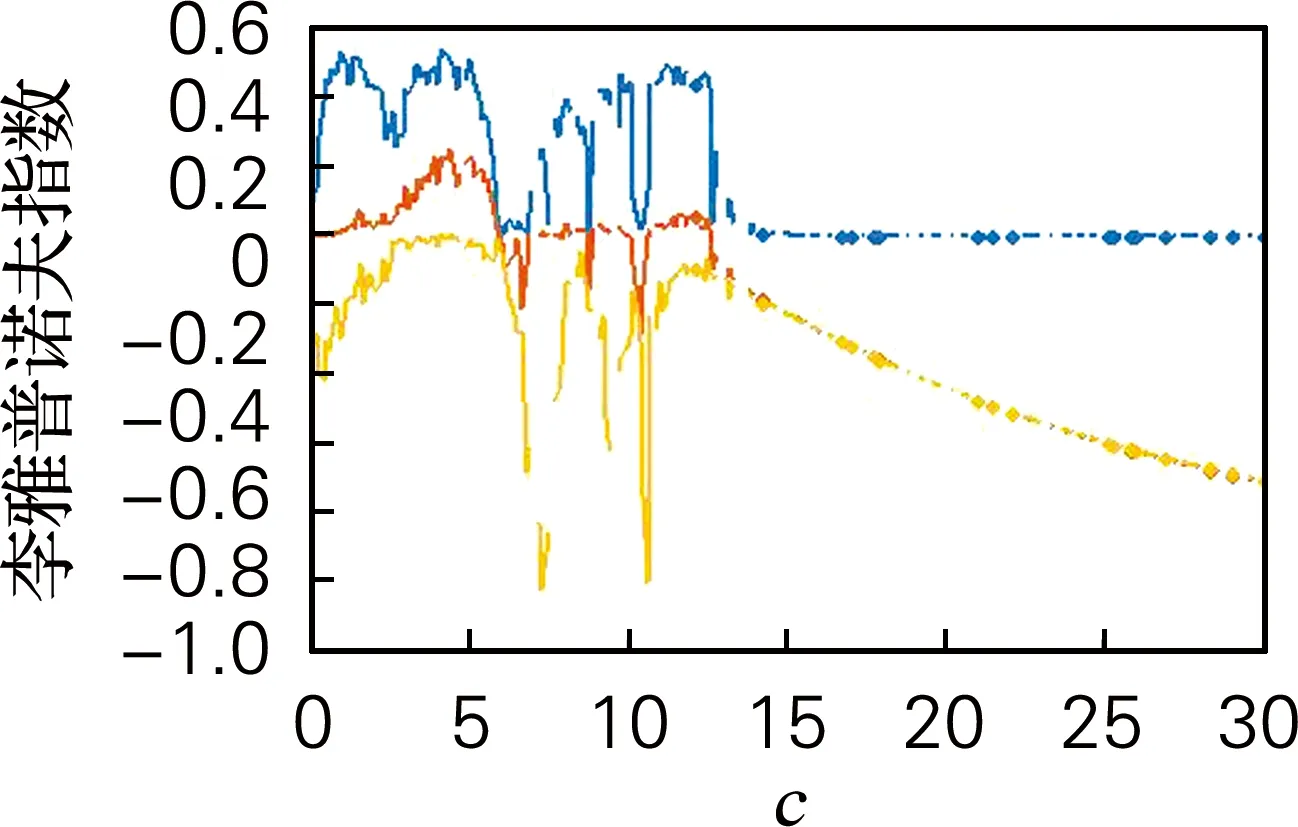
(a) 李雅普诺夫指数谱

(a) 李雅普诺夫指数谱

2.5 Poincaré截面图

图8展示了新超混沌系统在不同截面上的Poincaré映像。截面上的截点形成连续的线状或片状的稠密点集，进一步验证了该系统的混沌特性。

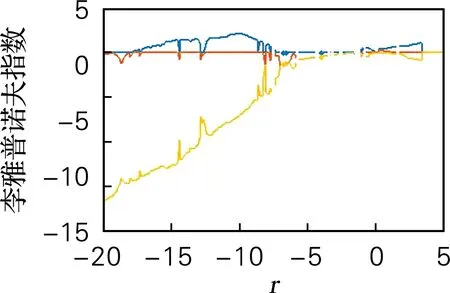
(a) 李雅普诺夫指数谱

3 新超混沌系统电路实现

超混沌系统的状态变量实际上是处于一个很大的动力学变化范围，在构建实际混沌电路时，这个范围超出了所使用的运算放大器所能提供的电压范围。由于变量替换并不会改变系统状态和特性，因此可进行适当的变化，令x1=x/50，y1=y/50，z1=z/50，w1=w/50。由此原系统可转化为

(4)

转化后的系统式(4)的电路方程为

(5)

(a) x=0(二维)

图9 新超混沌系统电路图Fig.9 Circuit diagram of new hyperchaotic system

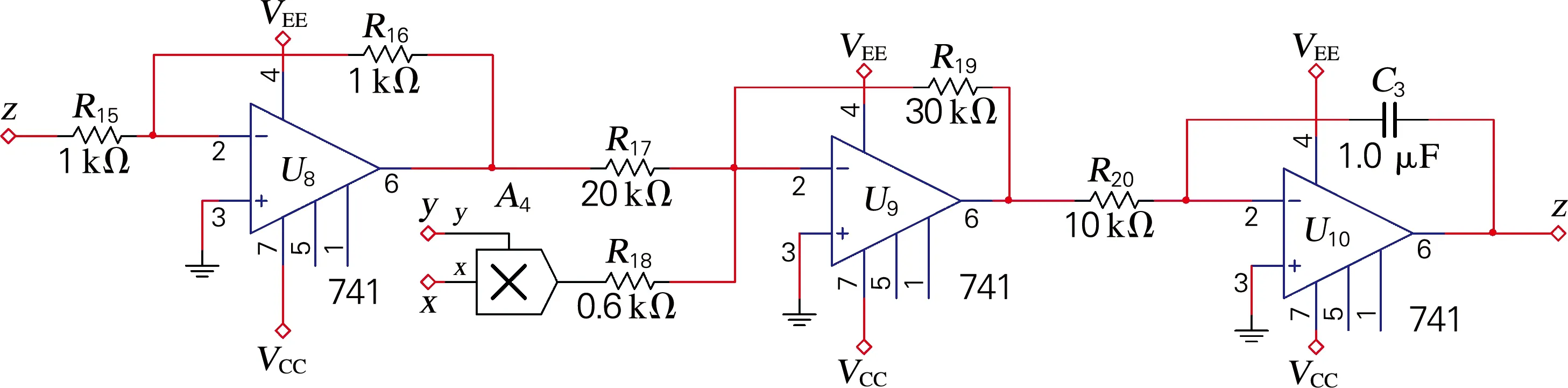
图9 (续)Fig.9 (Continuation)

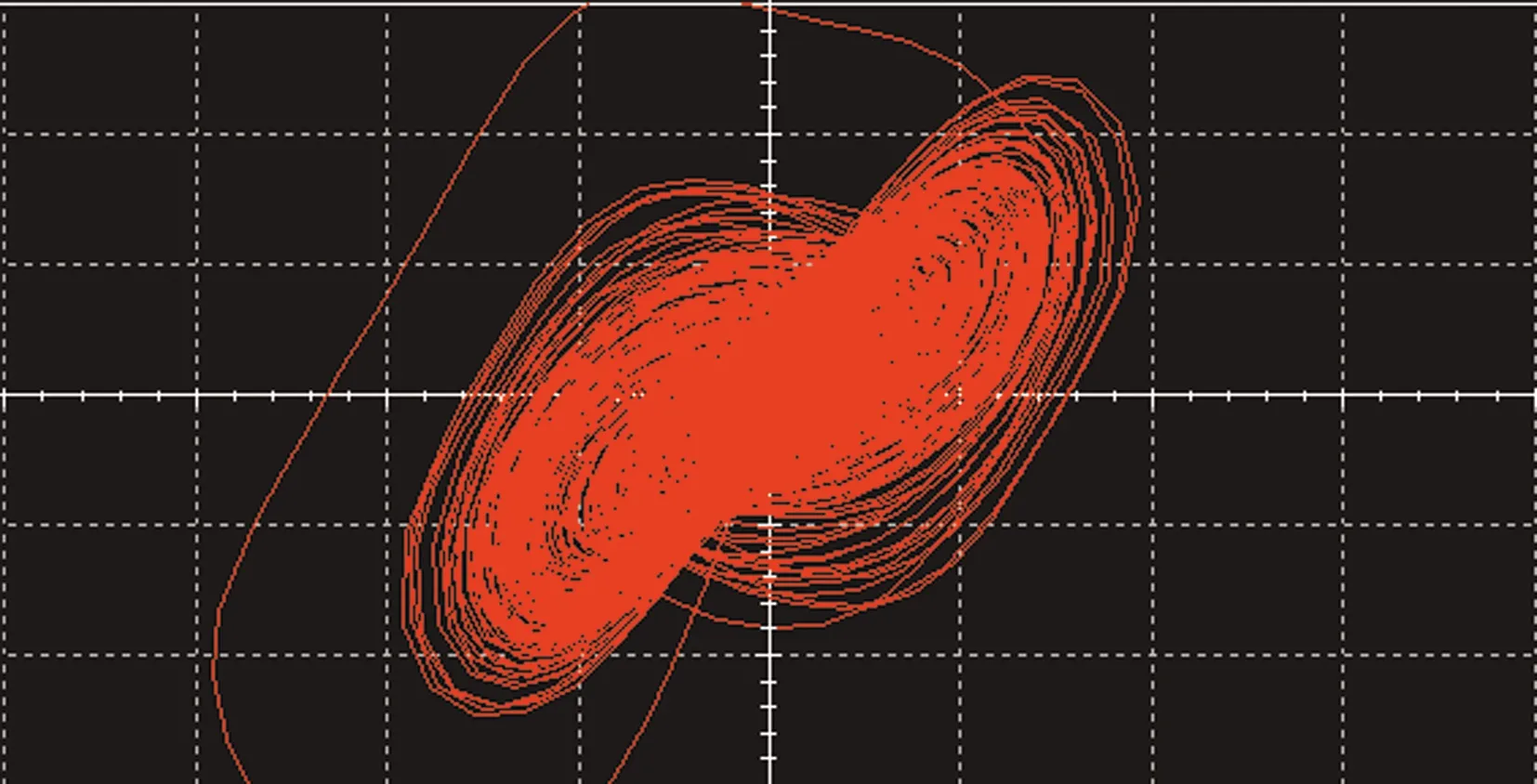
(a) x-y平面相图

4 复混沌系统

4.1 复混沌系统设计

(6)

当参数取a=15，b=1.5，c=5，d=43，r=0.5，e=3.5时，复混沌系统处于超混沌状态，其相图如图11所示。

4.2 复混沌系统的电路实现

基于Multisim构建复混沌系统仿真电路如图12所示。仿真结果如图13所示。对比图13与图11可见仿真结果一致，该复混沌系统在物理层面是可以实现的。

图12 复混沌系统电路图Fig.12 Circuit diagram of complex chaotic system

图12 (续)Fig.12 (Continuation)

4.3 李雅普诺夫指数及李雅普诺夫维数

复混沌系统式(6)的李雅普诺夫指数计算可得LE1=3.945 771，LE2=0.001 854，LE3=0，LE4=-1.289 807，LE5=-4.019 445，LE6=-9.318 841，LE7=-19.702 222，该系统有两个正的李雅普诺夫指数，因此是超混沌的，复混沌系统的李雅普诺夫指数图如图14所示。计算复混沌系统李雅普诺夫维数为4.661 2，为分数维，进一步说明该复系统是混沌的。

图14 复混沌系统的李雅普诺夫指数图Fig.14 Lyapunov exponents spectrum of complex chaotic system

5 结 论

构造了一个新的有5个可变参数的四维超混沌系统。随着参数改变，系统可以出现混沌吸引子、超混沌吸引子、周期、拟周期等丰富的动力学行为。将新超混沌系统的状态变量从实数域扩展到复数域，得到一个新的复混沌系统。用Multisim 设计实现了新超混沌系统及复混沌系统的仿真电路。电路仿真结果与数值分析结果一致，验证了新该系统的存在性和物理可实现性，为混沌系统在信息传递、超导、保密通信等领域的应用奠定了基础。

(a) x3-x5-x6三维相图

(a) x1-x3平面相图