输入转速波动下斜撑离合器的动态接合特性
严宏志,田昊,朱楚,李智,秦娟,刘建睿,王志标
(1.中南大学机电工程学院,湖南长沙,410083;2.中南大学高性能复杂制造国家重点实验室,湖南长沙,410083;3.中南大学轻合金研究院,湖南长沙,410083;4.中国航发湖南动力机械研究所,湖南株洲,412002)
PCE型斜撑离合器作为直升机传动系统中的关键部件,具有承载能力强、使用寿命长、过载防“翻滚”的优点。目前,国内外学者对斜撑离合器稳态工作的动静力学进行了研究。CHASSAPIS 等[1]基于接触力学理论,建立了离合器接合过程与传动状态下的非线性刚度动力学模型;XU等[2-4]分析了楔块与内外环的Hertz 接触应力,提出了楔块与内外环的接触为点-点接触,并得到了溜滑角与接触力的数学表达式;CHESNEY 等[5]研究了圆弧型面斜撑离合器楔角与内外环轨道半径差的关系,得到了接触压力和周向压力的数学模型;VERNAY等[6]分析了斜撑离合器楔块打滑的原因,同时得到了瞬时过载时的力学性能和楔块接触面的微小滑动现象;CENTEA等[7]考虑了斜撑离合器的几何尺寸、惯性和楔块与滚道接触力等因素,建立了非线性多体动力学模型,并分析了离合器扭转振动情况;CHEN 等[8]研究了不同规格楔块的斜撑离合器的接触特性[8]。朱自冰[9]基于经典弹性理论得到了全相位型斜撑式离合器楔角与接触应力应变的关系;朱楚等[10]分析了斜撑离合器内外环与楔块之间的磨损量和离合器楔角等结构参数的变化规律;扈文庄[11]基于Hertz 接触模型分析了楔块与内外环的接触应力,研究了楔块的设计与制造加工技术,同时推导得到了楔块的楔角函数;HUANG等[12]建立了多圆弧斜撑离合器动力学模型,并使用非线性迭代方法分析了不同时刻接触半径值及接触力。此外,严宏志等[13-19]对斜撑离合器进行了大量的研究工作,包括对单圆弧斜撑离合器力学特性研究,得到了接触应力沿楔块轴向变化的分布规律[13];建立了圆弧型面、对数型面和阿基米德型面3种内凸轮型面楔块的斜撑离合器的动力学分析模型[14];提出了对数型面斜撑离合器参数化设计方法,研究了基于磨损量的斜撑离合器失效判断依据,分析了存在实际制造误差的斜撑离合器的啮合特性[15-16];建立了对数型面斜撑离合器设计与分析的数学模型[17];研究了不同初始内楔角的阿基米德型面斜撑离合器的接触性能,并对楔块进行了型面修形优化[18];建立了斜撑离合器二轴总成系统的非线性振动模型,并为该系统的动态设计和振动控制提供依据[19]。本文作者针对离合器实际使用中存在的输入转速随机波动工况,采用有限元方法研究输入扰动下斜撑离合器动态接合特性,为离合器的设计与应用提供参考依据。
1 PCE型斜撑离合器结构与工作原理
斜撑式超越离合器主要包括全相位型(full phasing type)和强制连续约束型(positive continuous engagement type)2种类型[14]。强制连续约束型离合器相对全相位型离合器具有结构简单、承载能力强和过载防“翻转”等优点,其主要包括楔块、内环、外环、轴承、保持架、注油孔和弹簧。图1所示为PCE型离合器结构示意图。

图1 PCE型离合器结构示意图Fig.1 Schematic diagram of PCE clutch
PCE型斜撑离合器属于采用滚动摩擦原理工作的传动件,主要借助楔块与内外环的楔紧作用进行扭矩传递,其结构循环对称,局部模型剖面如图2所示。弹簧的扩张力提供了楔块的预紧力,当主动件外环的转速大于内环的转速时,楔块在摩擦力的作用下绕其中心顺时针旋转,此时,内、外环的径向差a小于楔块横截面的最长尺寸c,楔块楔入到内外环之间,离合器形成了闭锁组件,由此进行扭矩传递。当内环被动件的转速大于外环被动件的转速时,楔块将在摩擦力作用下绕其中心逆时针旋转,此时内外环的径向差a大于楔块横截面的最短尺寸b,楔块与内外环脱离楔住作用,离合器内外环相互独立转动进入超越状态。
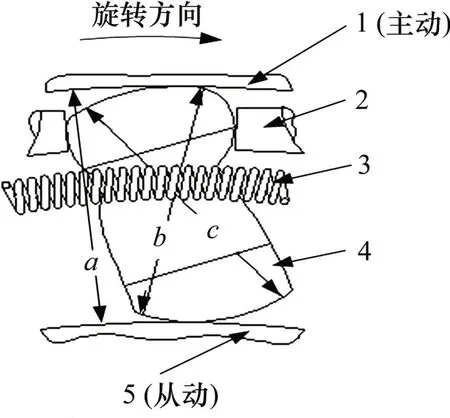
图2 PCE型离合器局部模型示意图Fig.2 Schematic diagram of local PCE clutch mode
2 PCE型斜撑离合器有限元模型建立
2.1 模型的简化与假设
根据PCE型斜撑离合器的结构特点和接触情况,对有限元模型进行假设简化:1)忽略离合器接触元件因温升而引起的热变形;2)忽略模型倒角、圆角等微小的几何细节对接触分析的影响;3)楔块与内外环滚道之间的接触摩擦遵守库仑摩擦定律;4)在离合器接触元件的整个接触过程中,摩擦因数不发生改变;5)PCE型斜撑离合器为循环对称的几何结构,共有33 个楔块,因此,本文取整体的1/33 进行仿真分析。
2.2 有限元模型的建立
1)几何建模。PCE型斜撑离合器楔块规格J=9.5,内凸轮面为双圆弧型面。离合器为循环对称几何结构,共有33 个楔块,通过楔块与内外环间的摩擦接触传递扭矩。利用Pro/E软件建立PCE型斜撑离合器1/33实体模型。
2) 材料属性。斜撑离合器楔块材料采用的是GCr15,内外环材料采用18CrNi4A,具体参数如表1所示。

表1 PCE型离合器材料属性参数Table 1 Material property parameters of PCE clutch
3) 接触定义。楔块与内外环均定义为变形体,接触定义设置如表2所示。

表2 PCE型离合器各部件的接触定义Table 2 Contact definition of each component of PCE clutch
4)网格划分。采用8节点的六面体线性缩减积分单元(C3D8R)对模型楔块与内外环进行独立划分网格,建立的PCE 型斜撑离合器有限元模型如图3所示。

图3 PCE型斜撑离合器有限元模型Fig.3 Finite element model of PCE clutch
5) 分析步(Step)与边界条件加载。Step 1 施加楔块辅助扭矩,用以模拟弹簧对楔块的支撑作用,使其与内外环紧密接触;Step 2 施加输入转速和负载扭矩;Step 3对输入转速引入随机波动干扰。在Step 1~3 中,给楔块施加0.04 N·m 的辅助扭矩,从Step 2 开始对外环施加712 rad/s 的输入转速,并给内环施加40.04 N·m 的负载扭矩,在Step 3 中保持负载扭矩不变,对输入转速分别加入5%,8%和10%的随机波,加载曲线如图4所示。设置完成后,采用ABAQUS中的显示动力学求解器进行模拟仿真[20]。
3 仿真结果与分析
3.1 输入转速随机波动对离合器接触特性的影响
斜撑离合器从Step 2 进入稳定运行状态,0.03 s时刻的楔块与内、外环工作面上的Mises应力分布如图5所示。
得到的楔块内外凸轮及内外环的Mises接触应力的分布曲线如图6所示,Mises 应力峰值数据如表3所示。
由图6和表3可知:1)楔块沿轴向Mises 应力呈现M 分布,而与之接触的内外环接触应力较均匀;2)楔块的等效Mises应力均大于内外环的Mises应力,平均约为内外环接触应力的1.6 倍。这是楔块与内、外环接触区域的曲率不同所致,实际情况中楔块也更易磨损;3)由于楔块与外环的接触面较大,外凸轮的Mises 接触应力小于内凸轮的Mises 接触应力,故后续研究中重点关注楔块内凸轮工作时的接触特性。
在负载扭矩不变的情况下,分别取内凸轮在轴向长度方向上2.8 mm 和19.2 mm 处应力峰值位置进行分析,研究输入转速在5%,8%和10%随机波动下楔块内凸轮的接触特性。

图4 加载曲线图Fig.4 Loading curves
图7所示为不同的输入转速波动下楔块内凸轮应力峰值处Mises 接触应力变化图。从图7可见:在恒输入速度段,Mises 应力在814~1 388 MPa 内小幅度变化;当输入转速5%波动时,Mises 接触应力波动较小;当输入转速8%和10%波动时,接触应力波动明显增大。表4所示为5%,8%和10%转速波动时Mises接触应力的波动特征值及与稳定时的比较结果。由表4所示标准差可知:8%转速波动造成的接触应力波动较大。
楔块与内外环的接触面积也是离合器接触特性重要指标之一。转速波动时楔块与内、外环接触面积变化如图8和表5所示。随着输入转速波动增大,接触面积的波动范围均差距不大。内凸轮与内环的接触面积小于外凸轮与外环的接触面积,解释了楔块内凸轮的接触应力大于楔块外凸轮接触应力的现象。

图5 楔块与内、外环的Mises应力分布云图Fig.5 Mises stress distribution cloud diagram of wedge and inner/outer rings

表3 楔块与内、外环的Mises应力峰值Table 3 Peak Mises stress of wedge and inner/outer rings
3.2 输入转速随机波动对离合器传动特性的影响
输入转速随机波动对输出轴转速跟随特性的影响规律如图9和表6所示。

图6 楔块内外凸轮与内外环的Mises应力分布图Fig.6 Mises stress distribution diagram of wedge inner/outer cam and inner/outer ring

表4 转速波动与稳定时Mises接触应力波动比较Table 4 Comparison of Mises contact stress fluctuationbetween rotational speed fluctuation and stability
由图9及表6可知:输出转速波动规律与输入转速波动的整体变化规律基本一致;当输入转速波动为5%,8%和10%时,转速跟随最大误差率分别为恒速输入时跟随误差率(5.35%)的1.7,2.5 和3.0 倍,说明输出转速跟随性对输入速度波动敏感。
输入转速随机波动对内、外环的扭矩传递特性的影响规律如图10和表7所示。
由图10及表7可知:在输入转速发生8%和10%波动时,传递扭矩将产生近50%的波动,极不利于稳定传递扭矩。

图7 输入转速波动下楔块内凸轮应力峰值处Mises接触应力变化规律Fig.7 Variation of Mises contact stress at stress peak value of wedge cam under fluctuation of input speed

图8 转速波动下楔块与内/外环的接触面积变化Fig.8 Change of contact area between wedge and inner/outer ring under rotational speed fluctuation
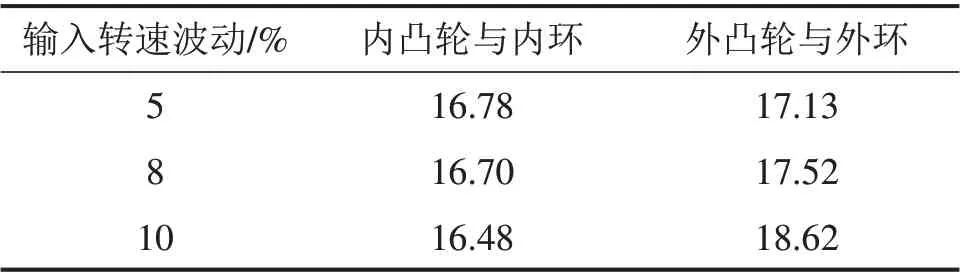
表5 内外凸轮与内外环单位时间内平均接触面积Table 5 Average contact area between wedge inner/outer cam and inner/outer ring in unit time mm2
4 实验验证
为了验证上述分析的结论,搭建如图11所示的斜撑离合器实验台,进行部分斜撑离合器的动力学测试实验。

表6 外环的最大/最小转速及误差率Table 6 Maximum/minimum rotational speed and error rate of outer ring
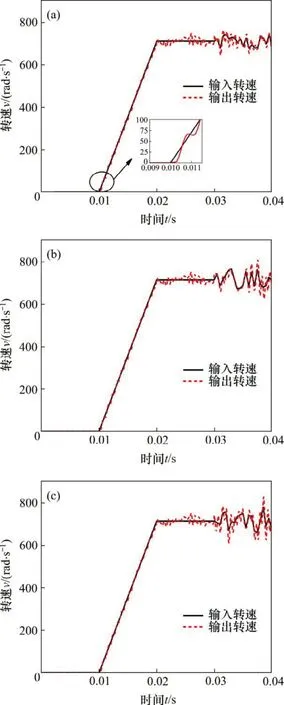
图9 不同输入转速波动下输出转速跟随特性Fig.9 Output speed following characteristics at different fluctuation of input speeds
设定驱动电机的输入转速为500 r/min(52.36 rad/s),负载电机的扭矩为15 N·m,测试不同转速波动下(0,5%和10%)离合器转速跟随特性,通过光栅尺测量输入输出转速,得到输入输出转速时域图,实验结果如图12所示,输出轴的最大最小转速及误差率见表8。

图10 不同输入转速波动下的扭矩传递特性Fig.10 Torque transfer characteristics different fluctuation of input speeds
由于斜撑离合器试验台存在安装误差及减速器等外界振动激励,故在设定的无转速波动下也存在传动误差,如表8所示。
从表8可知:当输入转速加入5%的波动时,转速跟随最大误差率与无波动时差距不大,传动较平稳;当输入转速波动增加到8%和10%时,转速跟随最大误差率明显增大,传动不平稳,表明实验结果与仿真结果基本吻合。

表7 瞬时扭矩传递最大/最小值及波动率Table 7 Maximum/minimum and error rate of instantaneous torque transfer

图11 斜撑离合器实验台Fig.11 Sprag clutch test bench

图12 不同转速波动下的实验结果Fig.12 Experimental results under different rotational speed fluctuations

表8 输出轴的最大最小转速及误差率Table 8 Maximum/minimum rotational speed and error rate of output shaft
5 结论
1) 离合器内外环的接触应力小于楔块的接触应力,且沿轴向分布均匀(楔块接触应力呈M型分布)。
2) 输入转速随机波动对斜撑离合器的接触应力影响明显,8%输入转速波动的标准差达到5%波动时的1.5倍。
3)当输入转速波动10%时,转速跟随最大误差率达到恒速输入时的3倍,说明输入速度波动对离合器输出转速稳定性影响显著。
4)当输入转速发生8%和10%波动时,传递扭矩产生近50%波动,对稳定传递扭矩极为不利。

