考虑不确定性和储能系统的虚拟电厂与能效电厂联合调度优化模型及仿真应用

牛东晓，赵东来，杨尚东，刘龙珠

(1.华北电力大学经济与管理学院，北京，102206；2.国网(苏州)城市能源研究院城市能源战略与规划研究所，江苏苏州，215000；3.国网能源研究院科研发展部，北京，102209)

随着世界能源紧缺、环境污染等问题日益突出，分布式电源(distributed generation，DG)以其可靠、经济、灵活、环保等特点而被越来越多的国家所采用。然而，尽管DG优点突出，但仍存在诸多问题，如容量小、数量大、分布不均匀等。分布式电源的接入给电网的稳定运行带来了许多技术难题，如潮流改变、线路阻塞、电压闪变等。若将DG 聚合成1 个集成的实体(integrated entity)则能够解决上述问题，主要解决途径包括微电网和主动配电网，但微电网受地理区域限制，对多区域、大规模DG的有效利用有一定的局限性[1]。人们对主动配电网将DG 的接入半径进行了一定的扩展，能够对配电网实施主动管理，但对DG 对大电网及电力市场的效益考虑不足[2]。虚拟电厂(virtual power plant，VPP)的提出则为解决这些问题提供了新的思路，通过先进信息通信技术，可实现DG、可控负荷、电动汽车等分布式资源聚合和协调优化[3]，形成电网运行的电源协调管理系统[4]。但虚拟电厂主要作用于发电侧，为了能够最优化虚拟电厂参与系统调度的优化效果，需要引导用户侧响应系统调度。能效电厂通过采用高效用电设备和产品、优化用电方式等途径，形成某个地区、行业或企业节电改造计划，降低用电负荷，等效产生富余电能，达到与实际电厂相同的效果[5]。能效电厂的实现形式在于需求侧的有效节能，而虚拟电厂的实现形式在于电源侧有效分配和管理DG发电和可控负荷，研究虚拟电厂和能效电厂的联合调度优化将对电力供需两侧对接模型的建立大有裨益[6]。对于EPP和VPP协同运行的研究，TAJEDDINI等[7]将VPP定义为连接到低压配电网络的热电联产发电单元的组合。JU等[8]提出了需求响应VPP 的概念，建立了基于价格的需求响应VPP 和基于激励的需求响应VPP，它考虑了运行限制条件和响应不确定性对系统成本的影响，有助于提高系统可靠性并减少系统风险成本。PANDŽⅠĆ等[9]指出，美国加利福尼亚州在2004—2013年实施能效工程，节省了5 GW发电容量，同时满足电力消费需求。王雁凌等[10]建立了节电潜力优化模型，从负荷转移和节电角度计算了EPP的节电潜力。张宁等[11]将EPP输出与负荷曲线分开，得到了纯负荷曲线，并将纯负荷曲线与传统发电厂停运概率表相结合。以上研究仅从单一前景和单方面讨论了需求侧和发电侧对VPP 和EPP 的影响，本文作者将VPP 与EPP 相结合，分析需求侧和发电侧的协同影响。

1 电源输出功率模型

1.1 风力发电出力模型

设定风速服从Weibull 分布，且根据风电场历史风速数据拟合风速Weibull 分布的尺度参数ξ与形状参数k。设随机变量为v，风速符合尺度参数与形状参数分别为ξ和k的Weibull分布[12]：

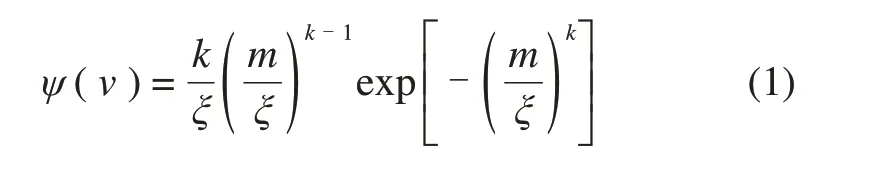
式中：m为风速。风电场的输出功率可由下式表示：

式中：为风电场原始模拟出力；min，mrated与mout

分别为风电机组切入风速、额定风速与切出风速；R为风电额定出力功率。

1.2 太阳能发电出力模型

光伏发电的基本原理是根据光生伏打效应，利用光伏板将太阳能转化为电能，出力可由下式计算[13]：

式中：gst为光伏发电出力功率；gstc为标准条件下光伏板的出力(太阳辐照强度Istc=1 kW/m2，温度θstc=25 ℃)；αθ为光伏板的功率温度系数；Ir,t为t时刻实际太阳辐照强度；θt为t时刻光伏板的温度。

1.3 储能系统出力模型

储能系统主要借助储能控制器跟踪蓄电池充放电行为。当蓄电池达到最大容量时，储能控制器会控制蓄电池停止充电；当蓄电池持续放电直至最小充电状态时，储能控制器会控制蓄电池停止放电。

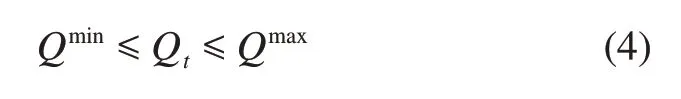
式中：Qmax和Qmin分别为蓄电池储存容量的上、下限；Qt为蓄电池t时刻的蓄电量。

当蓄电池处于放电状态时，有

当蓄电池处于充电状态时，有

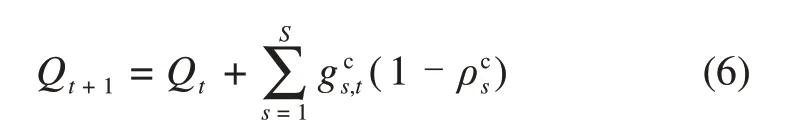
式中：S为蓄电池总量；s为蓄电池序数；和分别为储能系统中蓄电池s在t时刻的放电和充电功率；为蓄电池s在t+1时刻的蓄电量；和分别为蓄电池放电和充电损耗。

储能系统在充放电过程中会发生自身损耗，故在整个调度周期T内，储能系统的充电量与放电量之间的关系满足：

式中：Q0为储能系统初始时刻的蓄电量。

2 虚拟电厂和能效电厂双层调度模型

2.1 上层优化模型

设定虚拟电厂主要由风电、太阳能发电和燃气轮机发电构成。在分析虚拟电厂并网调度时，以系统总的发电成本最小为优化目标，具体目标函数如下：

式中：C为虚拟电厂发电成本；C1为火电机组发电成本，包括主要燃煤成本和启、停成本；C2为燃气机组发电成本，包括主要燃气成本和启、停成本。火电机组和燃气机组的法定成本函数为：

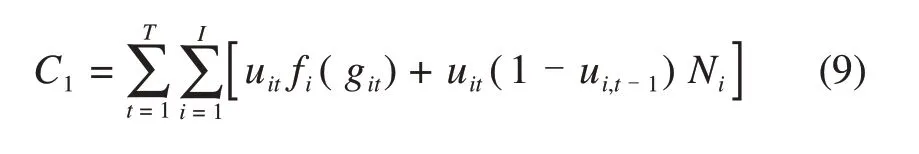
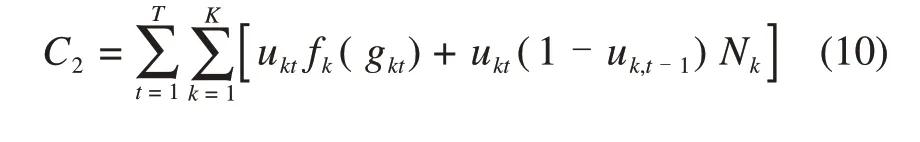
式中：git和gkt分别为火电机组i和燃气机组k在时刻t的发电出力；Ni和Nk分别为燃煤机组和燃气机组的发电启、停成本；uit和ukt分别为燃煤机组和燃气机组的发电启、停状态，uit为1表示机组处于运行状态，ukt为0表示机组处于停机状态；fi(git)和fk(gkt)分别为燃煤机组和燃气机组的发电煤耗成本函数，

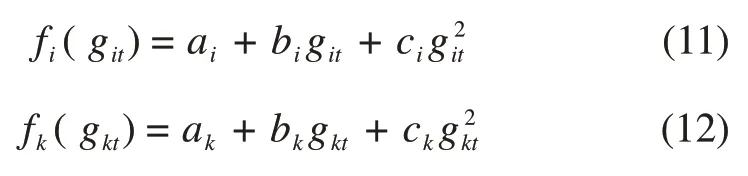
式中：ai，bi和ci为燃煤机组i的发电煤耗系数；ak，bk和ck为燃气机组k的发电煤耗系数，可由历史数据回归获得。

虚拟电厂参与下的系统发电调度优化模型既需要考虑传统发电调度模型的约束条件，又需要考虑虚拟电厂发电约束条件，主要约束条件如下。

1）电能供需平衡约束：

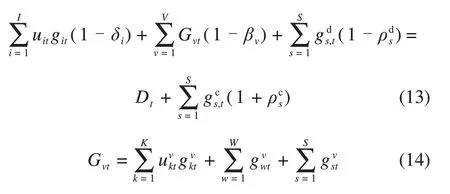
式中：Dt为系统时段t的系统负荷需求；Gvt为虚拟电厂v在时刻t发电出力；βv为虚拟电厂v的自身损耗；δi为火电机组发电厂用电率；，和分别为虚拟电厂v中燃气轮机、风电机组和太阳能发电机组在时刻t的发电出力。

2）火电机组出力约束：

式中：和分别为火电机组i的最大输出功率和最小输出功率；和分别为火电机组i的最大爬坡功率和最小爬坡功率；为燃煤机组i的最短启动时间；为t-1时刻燃煤机组i的连续运行时间；为燃煤机组i的最短停机时间。

3）系统备用约束：

式中：Rc表征不考虑虚拟电厂情形下的系统旋转备用能力；(gvt)和(gvt)分别为考虑虚拟电厂时上旋转备用和下旋转备用增加值，一般取原始负荷需求的10%作为新增备用。

2.2 下层优化模型

在下层模型中，主要讨论2种类型能效电厂：一是引入节电项目产生节电效果形成虚拟电厂，称为节能效率电厂(energy saving efficiency power plant,ESEPP)；二是用户参与需求响应产生的节电效果，称为需求响应效率电厂(demand response efficiency power plant,DREPP)。以能效电厂参与发电调度收益最大化为目标，综合考虑能效电厂发电出力约束条件，构建能效电厂参与调度优化模型，具体目标函数如下：

其中：π1和π2分别为DREPP 和ESEPP 参与发电调度获得的收益。设需求响应引入后的系统负荷需求Lt为

其中：ϑ和ρ为需求与价格的线性函数系数；πt为时刻t的需求响应收益。初始负荷和响应负荷可以被看作虚拟发电量，

式中：和Lt分别为需求响应引入前、后的系统负荷需求；为需求响应引入后负荷削减量，也称为DREPP发电出力，即虚拟发电机组的边际成本。ΔCt为虚拟发电机组的边际成本，

若将虚拟发电机组的边际成本作为能效电厂DR的结算价格，则可得到能效电厂DR的收益函数πt：

由式(25)可得到能效电厂DREPP参与发电调度获得的收益为

式中：T为总调度时间，一般取24 h。对于ESEPP来说，节电项目的引入需要投入一定的成本，在参与系统发电调度时，ESEPP参与发电调度单位发电成本为

式中：为ESEPP 单位电能投入的节能成本；Call为ESEPP 总的节能投入成本；Qall为ESEPP 在全寿命周期内总的节能电量。假定ESEPP 参与系统发电调度的结算价格为实时电价，则参与发电调度获得收益为

式中：Pt为实时电价；为能效电厂在t时刻的节约用电量。

ESEPP 和DREPP 的参与改变了需求侧负荷需求情况，在分析能效电厂参与发电调度时，既需要考虑传统发电调度约束条件，又需要分析能效电厂参与后增加的约束条件，具体如下。

1）负荷供需平衡约束：

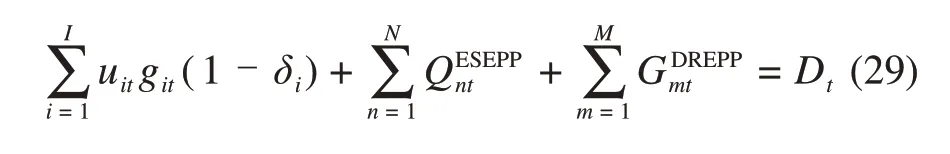
式中：和分别为第n个ESEPP 和第m个DREPP 发电出力；M和N分别为ESEPP 和DREPP 总数量。

2)DREPP 发电出力约束。DREPP 发电出力约束主要有最大削减量约束、发电功率约束约束、启停约束和最大出力功率约束。令总的负荷削减量ΔLt=则具体约束条件为

式中：vt为0～1 之间的变量，vt=1 表明负荷被削减，反之，表明未进行负荷削减；为t时刻负荷最大可削减量；LU和LD分别为能效电厂削减负荷量的爬坡功率上限和下限；和分别为负荷启、停时间约束；TU和TD分别为负荷的最小启、停时间；Mmax为能效电厂最大功率约束。式(32)为在时刻t最大负荷削减量约束。与常规机组相同，DREPP 同样要受到启、停时间的约束，否则可能导致负荷曲线波动性增加。式(31)和(32)分别约束了DREPP的爬坡上限和降坡上限；式(33)和(34)分别为DREPP启、停时间约束；式(35)约束了整个调度期内DREPP最大出力功率要低于一定的值，否则会给系统带来较大负担。

3) ESEPP 发电出力约束。ESEPP 发电出力约束主要为最大发电出力约束，令则

式中：Ot为0～1 之间的变量，vt=1 时表明负荷被削减，反之，表明未进行负荷削减；为t时段ESEPP 发电出力；为t时刻能效电厂最大负荷削减量。

4）系统备用约束：

式中：(ΔLt)和(ΔQESt)分别为考虑了能效电厂和虚拟电厂时系统新增上旋转备用容量；(ΔLt)和(ΔQESt)分别为考虑了能效电厂和虚拟电厂时系统新增下旋转备用容量。

3 算例分析

3.1 情景设定

为分析虚拟电厂和能效电厂的联合运行优化效果，设定4个仿真情景。

情景1：基础情景。该情景不考虑能效电厂，仅考虑虚拟电厂参与下系统发电调度优化模型。为分析储能系统对虚拟电厂并网的影响，本情景对比分析了储能系统引入前后的系统运行优化结果。储能系统最大充放电功率为80 MW，最大充电量为400 MW·h，充放电损耗为5%。

情景2：DREPP 情景。该情景讨论DREPP 和虚拟电厂联合参与下的系统发电调度优化模型。设定DREPP 最大可并网电量不超过负荷需求的15%，各时刻最大发电出力在原负荷的±20%之内。DREPP的运行参数参照文献[14]选取。

情景3：ESEPP情景。该情景讨论ESEPP和虚拟电厂联合参与下的系统发电调度优化模型。假设ESEPP 的单位发电投入成本为120 元/(MW·h)，实时电价为350 元/(MW·h)，ESEPP 最大可并网电量不超过负荷需求的15%，各时刻最大发电出力不超过原负荷的20%。

情景4：DREPP情景和ESEPP情景。该情景讨论DREPP，ESEPP 和虚拟电厂联合参与下系统发电调度优化模型。DREPP 和ESEPP参数与情景2和情景3的相同。

3.2 基础数据

虚拟电厂由3 个风电场、2 个太阳能发电站和2 台燃气轮机发电机组构成。风电场装机容量为200 MW，太阳能电站的装机容量为100 MW，2台燃气轮机发电机组装机容量为80 MW。燃气轮机的出力上、下限分别为20 MW 和80 MW，启、停时间间隔为2 h，爬坡功率为30 MW，参照文献[15]设定燃气轮机的发电成本函数。能效电厂主要由DREPP 和ESEPP组成，为分析虚拟电厂和能效电厂对系统调度的影响，选用文献[16]中4 台火电机组组成虚拟电厂和能效电厂组成仿真系统。

为了分析储能系统对虚拟电厂和能效电厂的优化效应，引入4个装机容量为100 MW的储能系统，每个储能系统充放电最大功率均为20 MW，储能系统充放电过程中自身损耗为5%[16]。表1所示为本算例中所设定的火电机组发电运行参数，图1所示为风电和太阳能发电出力。

3.3 仿真结果

为了分析DREPP 和ESEPP 共同参与对提升系统接纳虚拟电厂的优化效应，讨论DREPP，ESEPP 和虚拟电厂联合调度优化问题，能效电厂的运行参数与情景2 和情景3 的相同。图2和图3所示分别为DREPP 和ESEPP 共同参与下火电机组出力分布和虚拟电厂调度优化结果。

从图2可以看出：系统优先利用大容量火电机组满足负荷需求，例如G1和G2；小容量发电机组则在峰时段被调用，例如G3和G4，系统机组出力结构较优。这也说明DREPP 和ESEPP 能够替换原有火电机组为虚拟电厂并网提供备用服务，降低系统对火电机组的备用服务需求，并且虚拟电厂并网容量的增加也降低了系统的净负荷需求。

从图3可以看出：当引入ESEPP 后，DREPP 能够匹配负荷需求曲线，进行发电出力，这有利于平缓终端用户负荷需求，促进风电和太阳能发电。对比引入ESEPP前，风电和光伏发电分别增加438 MW·h和128 MW·h，燃气轮机发电降低125 MW·h。同样，ESEPP为系统运行提供更多的备用，使得燃气轮机发电仅在调峰需求较多时提供服务，如8:00—16:00，总的发电出力降低了125 MW·h，这说明ESEPP 和DREPP 同时参与虚拟电厂联合调度，能够发挥各自优势，提升系统接纳虚拟电厂的能力，有利于风电和太阳能发电的并网。

表1 火电机组发电运行参数Table 1 Thermal power unit power generation operating parameters

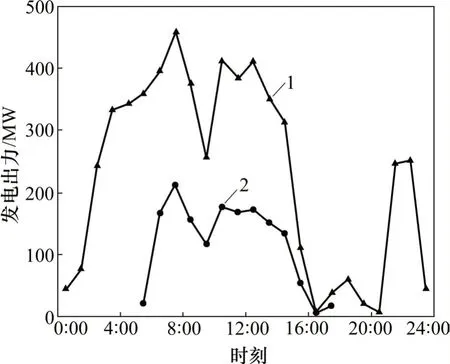
图1 风电和太阳能发电出力Fig.1 Available output of wind and solar power generation

图2 DREPP和ESEPP共同参与下火电机组出力分布Fig.2 Distribution of thermal power units with participation of DREPP and ESEPP

图3 DREPP和ESEPP共同参与下虚拟电厂调度优化结果Fig.3 Virtual power plant scheduling optimization results with participation of DREPP and ESEPP

3.4 对比分析

为深入分析能效电厂与虚拟电厂联合优化效果，本文整理了4种情景下系统运行结果，如表2所示。

就系统运行结果而言，与情景1相比，ESEPP的引入能够增加虚拟电厂的并网容量，在发电成本最小目标下，风电和太阳能发电并网电量要显著提升，燃气机组的并网电量有所降低。当虚拟电厂并网电量增加时，降低了系统的发电成本、弃风电量和弃光电量。图4和图5所示为4 种情形下风电和太阳能发电并网结果。

就风电和太阳能并网情况而言，当DREPP 和ESEPP同时引入后，风电和太阳能发电并网电量达到最大。单独引入DREPP 时，系统风电和太阳并网结果要优于单独引入ESEPP 时的并网结果，与前面分析结果一致，能效电厂的引入平缓了负荷曲线，为虚拟并网电量，克服风电、太阳能发电不确定性对系统接电厂并网提供了备用服务，增加了风电和太阳能发电的并网电量。表3所示为4种情景下火电机组出力结果。

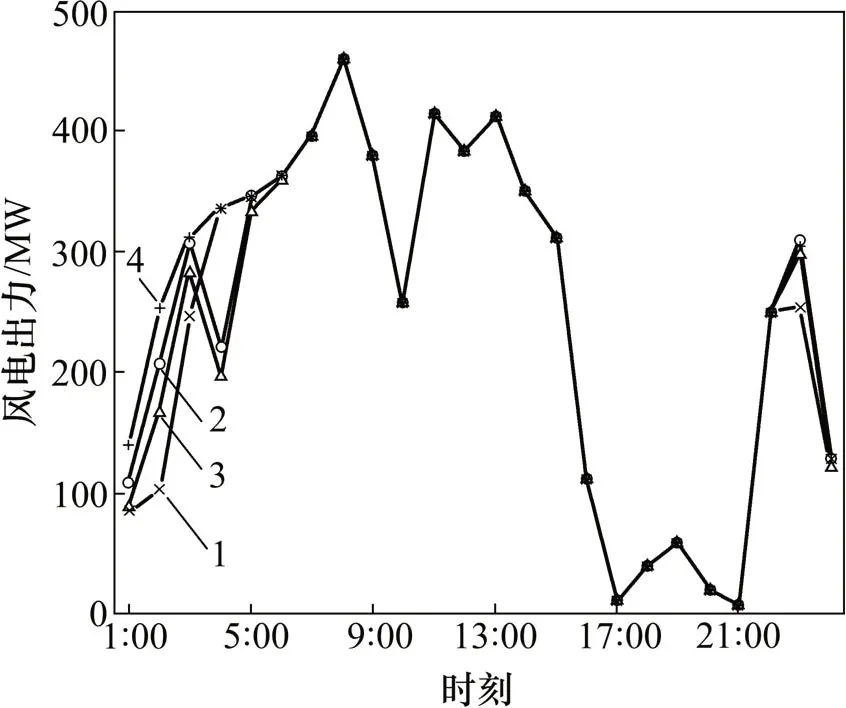
图4 4种情形下风电并网结果Fig.4 Wind power grid-connected results in 4 cases

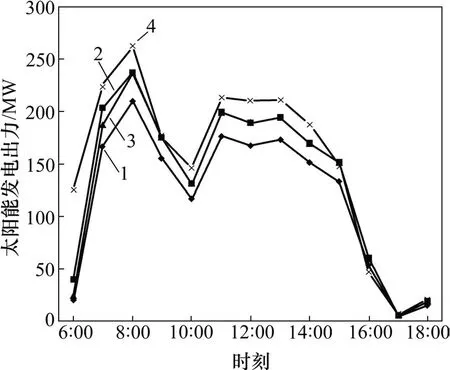
图5 4种情形下太阳能发电并网结果Fig.5 Solar power grid-connected results in 4 cases

从表3可见：利用能效电厂参与虚拟电厂并网发电调度能提升系统接纳虚拟电厂能力，增加虚拟电厂纳虚拟电厂的影响。为最大化利用可再生能源发电，将分布式能源聚合为虚拟电厂，并与能效电厂联合开展并网调度的途径值得推广。

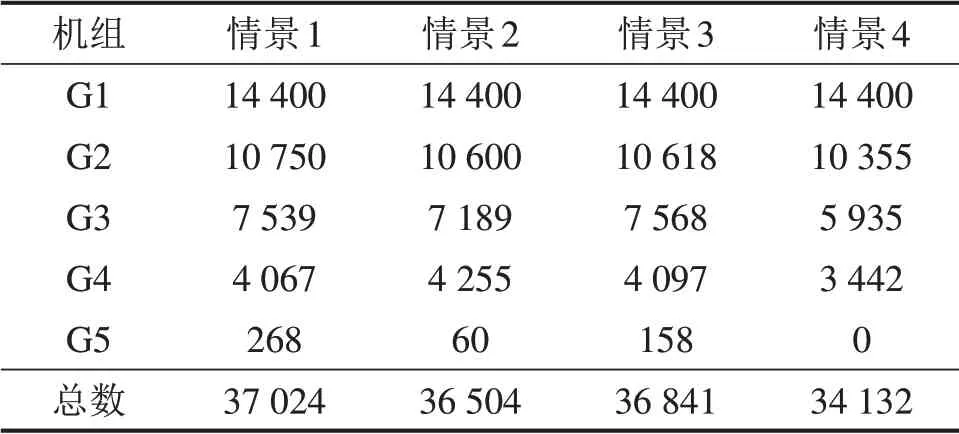
表3 4种情景下火电机组出力结果Table 3 Output results of thermal power units under four cases MW·h

4 结论

1) 构建了基于虚拟电厂与能效电厂的双层优化模型。将上层模型的优化结果传递给下层模型，下层模型根据上层结果调整自身参与调度策略，得到目标函数最优值，并反馈给上层模型实现动态博弈，最终达到全局动态最优解。

2) 将分布式能源打包以虚拟电厂的形式参与系统发电调度，能够解决分布式电源难以分配、控制和管理的问题，提升系统可靠性，并在增加系统消纳分布式能源能力的同时，降低系统发电成本。用户侧能效电厂的引入能够平缓负荷曲线，降低负荷曲线的峰谷差，为虚拟电厂的并网提供更大的容量空间。

3) 本文重点研究了能效电厂与虚拟电厂联合调度优化模型，但为了实现该优化调度过程，需要各参与方积极配合。如何根据各参与方贡献度进行效益分配是保证虚拟电厂和能效电厂联合调度的关键，这有待于进一步研究。