冻结方式对预冻甘露醇冰晶粒度分布的影响

贾颖姣，刘志强，罗春

(中南大学能源科学与工程学院，湖南长沙，410083)

真空冷冻干燥技术是目前最优良的干燥技术之一，冻干产品具有复水性好、稳定性高以及方便运输、长期保存等优点，因而在医药、食品、材料等领域得到广泛应用。但冷冻干燥耗时长、能耗大、设备初投资大，这些缺点制约了冷冻干燥技术的工业化发展。因此，优化冻干过程的工艺参数以提高冻干效率很有必要。真空冷冻干燥过程主要分为预冻阶段、升华干燥阶段和解析干燥阶段。其中，升华干燥阶段耗时最长，而预冻阶段的冻结方式是通过改变物料内部冰晶的尺寸来决定干燥层内孔隙的尺寸，对后期的干燥阶段尤其是升华干燥阶段产生影响，且冰晶分布的均匀度与干燥过程出现的空洞萎缩等现象有关。因此，人们对如何减少干燥时间、降低操作成本、得到高质量的冻干产品进行了研究。徐立冲等[1]研究了真空冷冻条件下停留时间、过冷度等对人工海水中冰晶生长速度的影响及作用机理；黄鸿兵等[2]研究了冻藏过程中-10～-20 ℃之间温度波动对猪肉肌间冰晶、颜色和新鲜度的影响，得出温度波动越剧烈，冰晶体积增大幅度越大，且-10 ℃恒温冻藏样品具有最小的直径；关志强等[3]对文蛤和波纹巴非蛤肉在-196，-78和-18 ℃中的冻结过程进行了研究，发现-78 ℃冻结使组织结构产生的冰晶较均匀，变形程度次之；骆丽君等[4]研究了不同冻结温度下面条内部水分分布、微观结构、冰晶形态等的变化，发现冻结温度越低，冻结速度越快，冻结时间和通过最大冰晶形成区域时间越少，面条内部冰晶体积越小，分布越均匀；LIN等[5]通过实验发现了使冻干脚手架的空隙分布与网状结构都好的最佳预冻温度；NAKAGAWA 等[6-8]通过模拟和实验证明了冻结过程中所建模型的正确性，并模拟出冻干速率和成核温度对冰晶尺寸以及干燥层渗透率的影响。上述研究大部分都是基于实验进行的，为了更深入地研究冷冻干燥技术，本文作者基于数值模拟进行系统研究，使生产者能根据具体需要制定最佳的冻结方式。

1 物理模型和控制方程

1.1 物理模型

目前，预冻方法有很多种，如冻干机内搁板冻结、冷库冻结、旋转冻结器冻结等，而冻干液态原料的生产用医药冻干机多采用干燥箱内搁板冻结[9]，且液态药品通常用西林瓶装排列置于搁板之上。因此，本文选取冻干机中两搁板间的1个西林瓶和它所分配的周围空间作为研究对象，具体物理模型及尺寸如图1所示。常温的药品溶液被装入西林瓶中放在搁板上，由上下搁板输送冷量使其冻结。在建模过程中进行如下假设：1)冻结过程只发生热传递，忽略质传递；2)传热方式主要为导热，忽略热辐射和热对流；3)西林瓶为圆柱形，且不考虑液面以上的瓶身和瓶口部分对换热造成的影响；4)冻结过程只发生在固液相界面上，其温度在固化温度和液化温度之间；5)冻结区域和液相区域各相物料分布且内部各处物性分别一致，忽略包含的不凝性气体；6)物料关于半径r=0呈轴对称，忽略物性的方向性差别；7)预冻后只有晶态，没有形成玻璃态物质；8)预冻阶段为常压；9)瓶内冰晶为异质成核，且温度一旦到达液化温度即开始结晶生长，即成核温度为271.28 K；10)忽略固相和液相的密度差异性，即冷冻前后溶液体积不变。

图1 西林瓶装物料预冻模型示意图Fig.1 Schematic diagram of pre-freezing material model in a vial

1.2 控制方程

预冻过程是一个相变界面随着时间移动的非稳态过程，即三维两相Stefan 问题[10-11]。本文运用多孔-焓法[12-14]处理相变潜热的问题。固液模糊区域被看作1个多孔区域，其中，某个小区域的孔隙率等于该处的液相体积分数，而液相的体积分数是基于热焓平衡法[15-16]计算的。能量方程如下：

式中：ρ为材料密度，kg/m3；H为焓，J/kg；u为流体的流速，m/s；k为导热系数，W/(m·K)；T为物料温度，K；φ为热源，W/m3。本文中u和φ都为0，液相导热系数k1和固相导热系数ks不同，材料的焓H为显焓h与潜热ΔH之和：

式中：href为参考焓值，J/kg；Tref为参考温度，K；cp为恒压比热容，J/(kg·K)。

式中：cp-s和cp-l分别为固相和液相的比热容，J/(kg·K)；Tsolidus和Tliquidus分别为固化温度和液化温度，K。糊化区域介于两者之间，某处已释放的潜热ΔH可按下式计算：

式中：L为潜热，J/kg。β为溶液的质量分数。

显然，ΔH在0～L之间变化。

耦合壁面边界条件如下：

1)当z=18 mm时，

2)当r=11 mm时，

式中：kg为空气导热系数，W/(m·K)；ρw为西林瓶壁面的密度，kg/m3；cp-w为西林瓶壁面的比热容，J/(kg·K)；Tw为西林瓶壁的温度，K；Tg为空气的温度，K；。

2 建模对象和计算方法

2.1 研究对象和内容

甘露醇作为一种保护剂，常被应用于冻干过程中[17-19]，因此，本文以体积分数为10%甘露醇作为研究对象，其用于模型计算的相关参数如表1所示。

为了研究不同冻结方式对冷冻之后物料内部冰晶颗粒粒度的影响，以生产中方便控制的搁板温度作为预冻过程工艺曲线的控制变量，设计3组不同的冻结方式：1)把物料放在搁板上冷却，搁板温度保持恒定(-10，-15，-20 和-25 ℃)；2)物料放在搁板上冷却，搁板从室温开始冷却且降温速率保持恒定(-0.5，-1.0，-1.5 和-2 ℃/min)；3)先使搁板温度由常温按照-1 ℃/min 的速度下降至一定养晶温度(0，-2，-4和-6 ℃)，并在该温度维持15 min，然后以-1 ℃/min的速度继续降温。

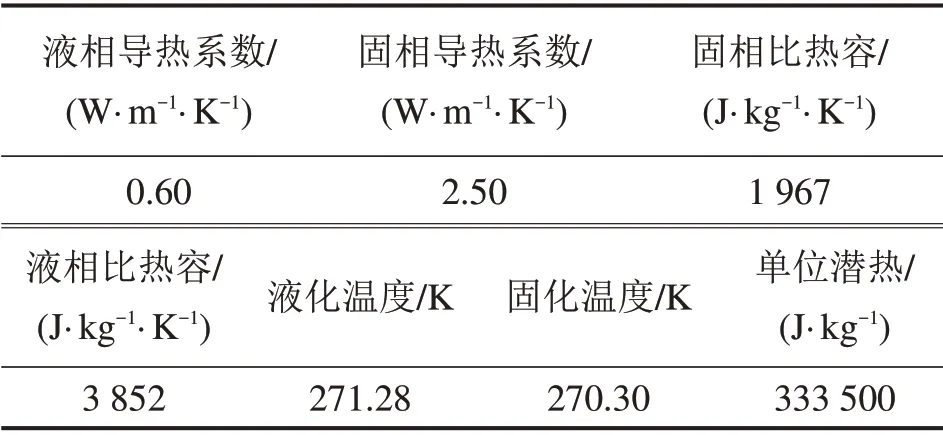
表1 10%体积分数甘露醇的物性参数Table 1 Physical properties mannitol with 10%volume fraction

2.2 结构模型设置和网格无关性验证

利用Ansys ICEM 软件建立几何模型。由于图1中该模型关于xz平面和yz平面对称，因此，截取整个模型的1/4划分网格，并设置对称边界条件进行计算。表2所示为4种计算网格数。在表2所示4种网格数量下，给出相同的边界条件，分别计算300 s 内甘露醇内部的温度变化，并选取中轴线(r=0)上z=1 mm这一点进行研究，其温度随时间的变化关系如图2所示。由图2可看出：当网格数为34.8万时，温度曲线出现明显波动；当网格数增加1倍时，波动趋势减小但仍能看到有几处凸点；当网格数增大到70 万时，曲线趋于平滑且网格数目对模拟结果的影响很小，可认为此时已达到网格无关。因此，考虑到计算速度和模拟结果准确性，本文后续的模拟工作均采用70 万网格进行计算，且都为六边形结构化网格，平均网格连长为0.2 mm，并按照需求在相变区域局部加密。

表2 4种计算网格数Table 2 Four kinds of grid numbers used in calculation 104个

2.3 计算方法和模型验证

在以上模型的基础上，基于Ansys Fluent 15.0 软件，采用有限体积法的二阶迎风格式进行控制方程的空间离散化，运用迭代法对相变区域温度进行求解，其中，残差设置为低于10-6，从而得出温度场。

相变域内温度分布有一定的特点，取预冻条件为搁板温度恒定-15 ℃进行研究。120 s和2 625 s这2个时刻的3 条径向线(z分别1，9 和17 mm)温度分布如图3所示。由图3可得：西林瓶内径向温差很小(最大温差约为1.12 ℃)，因此，本文以纵向中心线上的点为对象研究每一层温度以及粒度分布情况。

图2 点(0,0,1)用4种网格数得出的温度-时间图Fig.2 Temperature-time diagrams of point at(0,0,1)with four kinds of grid numbers

在溶液的中轴线上(即r=0 且0≤z≤18 mm)，每隔2 mm 取1 点观察其降温及相变过程中温度随时间的变化，结果如图4所示。得到温度变化曲线后，利用每个点冻结完成的时间计算相界面通过该点时的移动速率R，由图5中折线段的斜率表示。

相界面经过上述观测点时西林瓶内的温度场如图6所示。从图6可见：ti越大，则温度分布越趋于均匀，对应时刻的冷冻区域温度梯度Gi由此得出。

一些研究者研究了冰晶颗粒的粒度D与相界面移动速率R和温度梯度G之间的关系。例如，在金属凝固过程中，KURZ等[20]得出D∝R-1G-1或者D∝R0.5；对于苹果冷冻，BOMBEN 等[21]得出D∝R-0.5G-0.5；对于淀粉凝胶，REID[22]得出D∝R-x；对于明胶冷冻，WOINET 等[23]通过理论推导和实验验证得出D∝R-0.5G-0.5；对甘露醇冷冻，NAKAGAWA[6]运用关系式D=cR-0.5G-0.5对冰晶粒度进行计算，并用实验证明了其适用性。本文采用如下关系式计算冰晶粒度：

图3 温度恒为-15 ℃时不同时间3条径向线的温度分布Fig.3 Temperature distribution of three radial lines at different time when the temperature is constantly-15 ℃

图4 温度恒定为-15 ℃时的温度(T)-时间(t)关系曲线Fig.4 T-t diagrams when temperature is constantly-15 ℃

图5 温度恒定为-15 ℃的相变界面位置变化曲线Fig.5 Variation of position of freezing front versus time with shelf temperature of-15℃

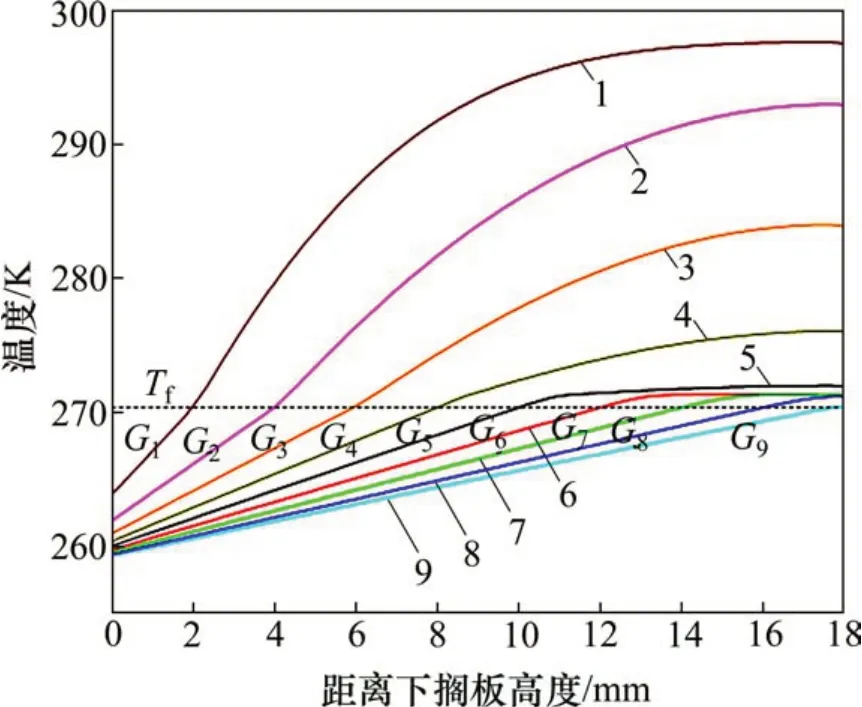
图6 不同时间西林瓶内温度分布Fig.6 Distribution of temperature in a vial at different time

其中：c为常数；R为相界面移动速率，mm/s；G为温度梯度，K/mm。

为了验证模型以及数值解的正确性，用该方法对文献[6]中的同类型实验进行模拟。在计算区域中，各介质的相关物性参数依据NAKAGAWA等[6]提供的参数设定，边界条件设定如下：初始温度为280 K，下搁板温度下降控制为-0.72 K/min，上搁板和四周空气壁面温度为80 K 恒温，温度场数据在MATLAB 中进行处理得到冰晶粒度分布，并对模拟的不同位置的粒度与其进行比较。选取3 个点的冰晶粒度进行对比，分别为A(0，0，2)mm，B(0，0，4)mm 和C(0，0，6)mm，结果如表3所示。

表3 模型验证结果Table 3 Validation results of model

运用该模型模拟得出粒度随高度的分布趋势与参考文献[6]中的一致，且由表3可知，仿真计算得到的冰晶粒径与参考值之间的误差在允许范围之内，表明该仿真计算的结果具有可靠性。

3 模拟结果与分析

在第1 种冻结方式(即搁板温度恒定)下，西林瓶中粒度分布如图7所示。由图7可得：粒度随着高度增加呈现先增大后减小的变化趋势，在z=16 mm附近达到峰值。不同温度下的冰晶粒度分布见图8。从图8可见：搁板温度Tb越低，则平均粒度D′ 越小，标准差S也越小；随着温度降低，平均粒度和标准差曲线都都趋于平缓，即要使西林瓶内粒度小且分布均匀，则可以适当调低搁板温度。但若温度过低，则会造成能源浪费，效果也不明显，且有可能使冷冻材料转为玻璃态[24]，影响之后的干燥过程。

图7 恒温时西林瓶纵向冰晶粒度分布模拟Fig.7 Simulation of ice crystal size distribution in vial vertical direction with constant shelf temperature

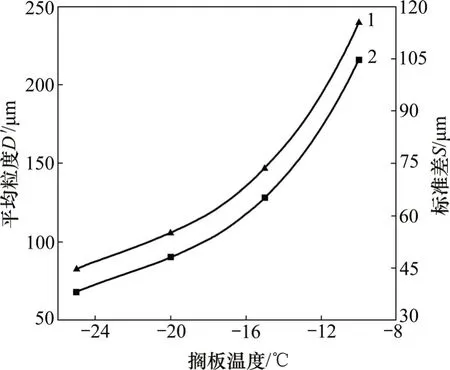
图8 恒温时冰晶粒度平均值D′和标准差S与温度的关系Fig.8 Mean value and standard deviation of ice crystal size distribution versus temperature

图9 恒定温降时西林瓶纵向冰晶粒度分布模拟Fig.9 Simulation of ice crystal size distribution in vial vertical direction with constant shelf temperature drop

在第2 种冻结方式(即搁板温度以一定的速度下降)下，恒定温降时西林瓶纵向冰晶尺寸分布模拟见图9，恒温时冰晶粒度平均值和标准差与降温速率的关系见图10。从图9和图10可见：西林瓶内纵向粒度分布也呈先增大后减小趋势，在z=16 mm附近达到峰值。对比搁板恒温和搁板恒定降温速率2种冻结方式，当选定相同的目标温度时，第2种冻结方式比第1种冻结方式得出的平均粒度更大但分布更均匀。例如，当降温速率v为-0.5 ℃/min 时，温度达到-25 ℃时物料已全部冻结即冰晶粒度分布已形成，此时，冰晶的平均粒度为130.25 μm，标准差为19.44 μm，而在恒温条件下即温度为-25 ℃时，冰晶的平均粒度为82.85 μm，标准差为38.19 μm。

图10 恒温时冰晶粒度平均值D′和标准差S与降温速率δ的关系Fig.10 Mean values and standard deviation of crystal size distribution versus temperature drop

在第3 种冻结方式(即搁板温度先由常温以速度-1 ℃/min 下降到某一养晶温度Tm并保持15 min，然后以相同的温度下降)下，含不同养晶温度时西林瓶纵向冰晶粒度分布模拟结果见图11，含不同养晶温度时冰晶粒度的平均值和标准差和与养晶温度的关系见图12。从图11和图12可知：当养晶温度为0 ℃和-2 ℃，这时的养晶温度均高于甘露醇溶液的凝固温度，西林瓶内粒度分布曲线几乎是重合的，2种养晶温度下得到的平均粒度以及标准差也近似相等；当养晶温度为-4 ℃和-6 ℃，这2 个养晶温度都低于甘露醇溶液的凝固温度，最大冰晶粒度出现的位置并不相同。此外，其他位置的冰晶粒度分布比较均匀，这是因为养晶温度变小。由此可见，养晶时间是调控冰晶粒度的1个重要因素。

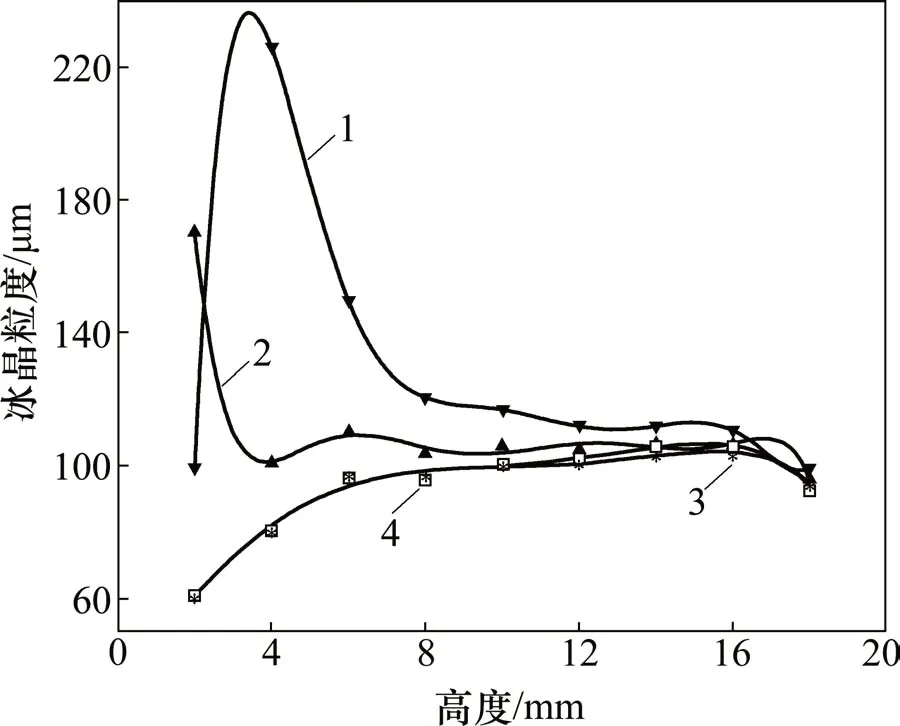
图11 含不同养晶温度时西林瓶纵向冰晶粒度分布模拟Fig.11 Simulation of ice crystal size distribution in vial vertical direction with different crystal growing temperatures

图12 含不同养晶温度时冰晶粒度的平均值D和标准差S与养晶温度的关系Fig.12 Mean values and standard deviation of ice crystal size distribution as functions of crystal growing temperature

与第2种冻结方式中降温速度为-1 ℃/min的情况相比，含养晶阶段的恒温降(即第3 种冻结方式)会使得平均粒度变大，若养晶温度高于凝固温度，则几乎不影响粒度分布的均匀度；要使均匀度发生变化，则可适当调节养晶温度，使其低于凝固温度并控制养晶时间。

4 结论

1) 建立了冻干箱预冻西林瓶装体积分数为10%甘露醇溶液三维仿真模型，利用Ansys软件模拟了该模型在预冻过程中的温度场，并通过Matlab 计算得到冻结后冰晶粒度的分布。

2) 在搁板恒温条件和匀速降温条件下，粒度分布沿西林瓶高度方向都呈中间大、两端小的变化趋势，峰值出现在略低于物料与空气界面处；随着搁板温度降低以及降温速度加快，平均粒度减小，分布更加均匀，同时减小的趋势逐渐变平缓；当选定1个目标温度时，匀速降温的方式比保持恒温得出的冰晶粒度更大但更均匀；匀速降温且当温度到达稍高于凝固点的温度时，加入一定的养晶阶段可增加平均粒度而不影响均匀度，要增大某些位置的粒度或调整均匀度，可视具体情况从降低养晶温度以及调整养晶时间方面着手研究。

3) 本文研究可为工程实际中冻结方式的选取提供参考和指导，也为深入研究冰晶粒度对冻干过程中干燥过程的时间和冻干产品质量的影响从而优化冻干曲线提供参考。