基于能量守恒法测试汽车的空气阻力系数

平培力，杜伟涛，胡玉梅

(重庆大学机械传动国家重点实验室，重庆，400044)

随着人民生活水平的提高，汽车保有量逐年增高，给营造蓝天白云的理想生活环境造成了极大的压力，因此，当前各国都在大力实施节能减排的工作，提高汽车燃油经济性、减少尾气排放是汽车行业发展与研究的主要方向之一。汽车在行驶中遵循能量守恒定律[1]，空气阻力作为汽车行驶过程中的主要有害阻力之一，降低了汽车能源利用率，而且车辆速度越高，空气阻力对车辆的影响越显著[2]。因此，对于汽车企业及相关研究人员而言，在设计阶段准确地依据汽车的空气阻力系数对车辆进行改进设计具有重要的现实意义。汽车滑行试验作为检验车辆燃油经济性的重要手段，不仅可以衡量汽车尾气排放量[3]，也可以监测到汽车轮胎与路面间的滚动摩擦阻力[4]、加速阻力、空气阻力[4-5]等，为提高汽车燃油经济性，减小汽车阻力、行驶中造成的能源浪费提供改进思路[6]；PETRUSHOV[3]基于时间-距离函数的方法，确定不受减速误差影响的滑行方程，改进了车辆空气阻力和滚动阻力；HUERTAS 等[7]使用广义简约梯度法对基于SAE 标准车辆滑行测试的数据进行分析，得出了汽车行驶阻力系数。ALJURE 等[8]使用移动监测设备对影响汽车空气动力学的各因素进行了测量；MCAULIFFE等[9]采用高/低迭代法对车辆滑行测试数据进行了分析，提出了提高空气阻力系数测试精度的方法；周宽容等[10]对空挡滑行试验数据进行处理，利用二次曲线方程求解出了被测车辆的滚动阻力系数和空气阻力系数；刘福才等[11]利用遗传算法和迭代方法处理滑行试验所得数据，并求得汽车的滑行阻力系数；周锋等[6]则利用功率法对行驶中的车辆进行了风阻系数的测定；PIKULA等[12]在开放式风洞中测量了不同风速下车辆的空气阻力，获得了车辆的空气阻力系数；田红旗[13]利用风洞试验研究了大风环境下的列车空气阻力特性；XIANG 等[14]研究了一种新的车载实验装置在风洞中的实验方法，分析了侧风对汽车动力学特性的影响。当前学者已采用试验方法、数据拟合、迭代方法等来标定车辆行驶中的阻力系数，提出相应的车辆阻力系数表达式，并已有一些研究成果，但缺乏高效、经济、方便易行的监测空气阻力系数的方法，特别缺少针对国家标准汽车滑行试验中空气阻力系数分析的方案。本文作者通过对被测车辆进行滑行阻力受力分析，利用能量守恒法构建了被测车辆的能量守恒关系，从理论上推导空气阻力系数的关系式，并对其合理性与正确性进行试验验证。

1 滑行阻力数学模型

文中以某型SUV 为研究对象，在对其进行道路滑行试验时，根据标准要求，车辆在平直道路上做滑行测试，因此，车辆的道路载荷包含滚动阻力、传动系阻力、空气阻力[11]，则其受力分析如图1所示。图1中：Ff为汽车滚动阻力；FN为车轮受地面支撑力；Fd为空气阻力；Ft为传动系阻力；Ga为被测汽车的总重力，N；v0为汽车前进速度，m/s。根据图1中的受力分析，基于能量法建立下式所示的能量守恒方程。

式中：Ea为汽车总能量；Ef为汽车滚动阻力消耗的能量；Et为汽车传动系阻力消耗的能量；Ed为空气阻力消耗的能量。

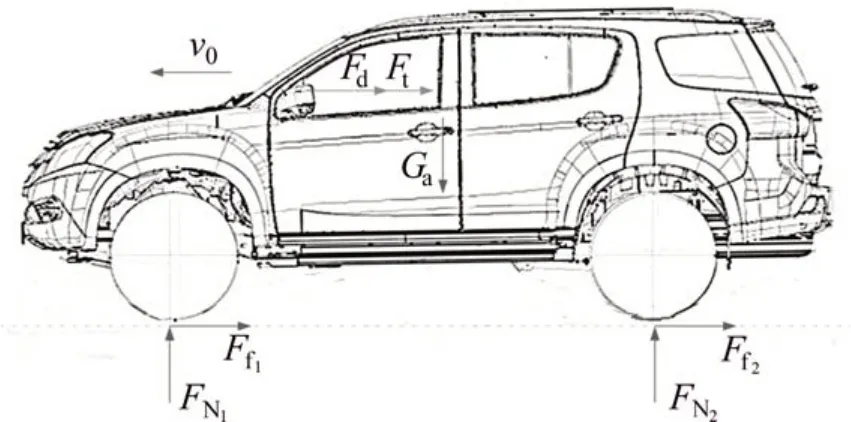
图1 汽车道路滑行试验受力分析Fig.1 Mechanical analysis of vehicle coast down

根据国Ⅵ排放标准测试要求[15]，被测车辆被加速至标准要求速度，做空挡滑行，同时监测被测试车辆的速度和滑行时间，得到速度与时间的关系式，则Ea的计算式为

式中：m为被测汽车的总质量，kg。

对于汽车滚动阻力消耗的能量，可以表示成用速度表示的积分形式，如式(3)所示：

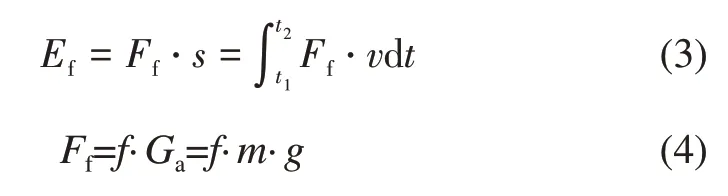
式中：s为汽车滑行位移，m；f为轮胎与地面间的滚动摩擦因数；g为重力加速度，1g=9.8 m/s2。

汽车在道路滑行试验过程中，车辆传动系阻力Ft带来的能量消耗同样可以表示为用速度表示的积分形式，如下式所示：

汽车在道路滑行试验中，空气阻力作为汽车阻力中的重要组成部分，汽车在道路滑行过程中所消耗的能量如式(6)所示：

式中：CD为空气阻力系数；A为汽车迎风面积，m2；ρ为空气密度，ρ=1.225 8 kg/m3；H为测试汽车的高度，m；B为测试汽车的宽度，m。

将式(2)～(7)代入式(1)可得确定空气阻力系数的式(8)。

从式(8)可看出得到车辆的速度随时间变化函数、传动系阻力、滚动阻力，即可求解出被测车辆的空气阻力系数。

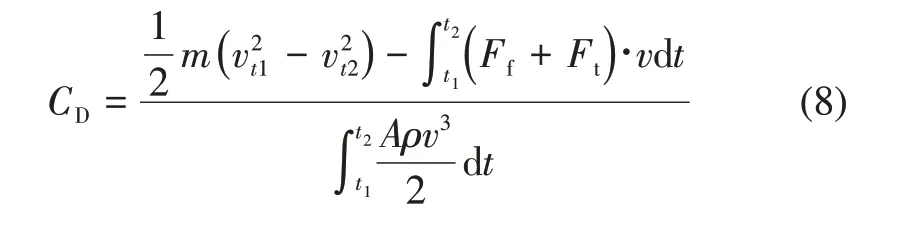
2 试验及数据采集

2.1 滑行试验

以某公司的某型M1类样车为试验对象，样车主要参数如表1所示，其中测试设备质量忽略不计，被测车辆行驶里程为15 000 km，并按照GB/T 12536—2017“汽车滑行试验法”和GB 18352.6—2016“轻型汽车污染物排放限值及测量方法(中国第六阶段)”[15]测试标准对其进行保养和四轮定位等试验前的准备工作。经检查符合要求的车辆，在具有国家试验认证资质的重庆机动车强检试验场性能试验路进行道路滑行测试，测试道路为平直道路，测试场地及监测仪器布置如图2所示。

图2 测试场地与环境测试仪器布置Fig.2 Test site and environmental test instrument layout

在设计被测样车的基准速度时，国Ⅵ标准[15]中规定：从20 km/h 起，步长10 km/h 增加，最高为130 km/h；若最高基准速度加上14 km/h(即144 km/h)大于等于最高车速，则应选择次高基准速度(即120 km/h)为最高基准速度，以此类推。

在每次滑行试验前，车辆加速到比最高基准速度高10～15 km/h的车速，稳定维持至少1 min后开始滑行。在滑行过程中，变速箱置于空挡，方向盘不转动，不进行制动，试验仪器以≥5 Hz的频率记录试验车辆的时间和车速。多次重复此试验，根据场地情况进行分段滑行(车况保持不变)，直到试验数据满足统计学精度要求。对应基准速度vj，读取仪器测量的车速从(vj+Δv)滑行到(vj-Δv)的时间，其中速度变化量Δv≤5 km/h。

往返双向进行滑行试验，测量至少3对往返的时间结果，其数值需要满足下所示的统计精度：

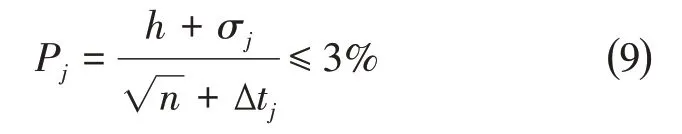
式中：Pj为基准速度vj下测试的统计精度；n为测试的组数；σj为标准偏差；h为系数；Δtj为基准速度vj的算数平均滑行时间，s。

对于式(9)中的系数h，GB 18352.6—2016[15]中以表格的形式给出了一系列数值。Δtj的计算按照下式进行计算：

式中：Δtji为基准速度vj的第i对测试滑行时间的调和平均值；Δtjai和Δtjbi分别为基准速度vj下第i对测试滑行在各自方向上的滑行时间。

标准偏差σj由数理统计公式使用此试验结果可表述为

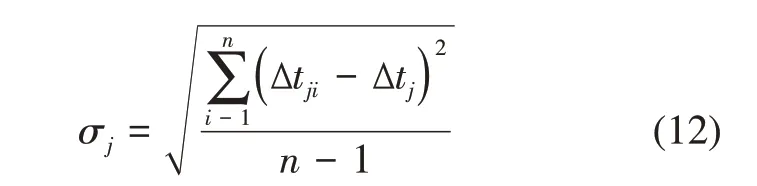
研究表明[16]，车辆滑行试验时，滑行速度对空气阻力系数有一定的影响。根据车辆状况和测试道路条件，对被测车辆采取三段滑行实验法进行道路滑行试验。滑行试验的起始车速为135 km/h，结束车速为15 km/h。在实际试验中，车辆滑行开始的最高车速需≥145 km/h，滑行结束的最低车速需≤10 km/h。本次滑行试验受试验场地长度限制，分3段进行，重复8次试验，记录基准点的滑行速度和时间。

表1 样车参数及测试环境Table 1 Parameters of sample vehicle and testing environment

表2 根据n确定的系数hTable 2 Coefficienth determined based on valuen

所得到的8组试验数据中，符合式(9)精度要求的有效试验数据共计6组。根据前述的试验条件分别归类整理这6组试验数据，可得到12次正、反向完整的滑行试验数据。

2.2 底盘测功机试验

汽车行驶中的传动系阻力主要由机械传动阻力和液力阻力2 部分构成[17]。根据以往研究经验[17-18]，传动系阻力随速度变化的关系服从一次线性方程, 即Ft=Ft0+Ft1v。利用底盘测功机反拖测试得到汽车的传动系阻力，并按照上述一次线性拟合可以得到传动系阻力随速度变化的关系式为

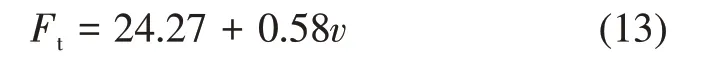
3 数据分析与验证

通过滑行试验得到了被测车辆的离散速度，根据底盘测功机试验和速度可得到传动系阻力Ft，为了实现式(8)所示的空气阻力系数CD的求解，还需确定式中的滚动阻力Ff。进行动力学分析时，一般借助经验公式估算滚动阻力系数[17]，估算轿车轮胎在良好硬路面上的滚动阻力系数为

当v<50 km/h时，f=0.015。

3.1 构建速度函数

在车辆的滑行试验中，由于采用了分段滑行测试，在高速滑行与低速滑行的联接区域的数据存在奇点数据。经过反复计算并参考文献[19]，以速度50 km/h 为基准，将第2 节中获得的有效滑行试验数据进行划分，以避免奇点数据对后续计算的干扰。滑行试验速度和时间之间的数值关系拟合结果如图3所示。

3.2 空气阻力系数求解

根据第1 节中推导得出的空气阻力系数计算式(8)，并利用第2节传动系阻力的研究成果、滚动阻力系数的经验值和3.1中的速度函数拟合结果，对式(8)中的空气阻力系数进行求解。将图3中得到的速度函数回代到式(8)中，并利用滑行试验数据对式(8)进行分段(步长为10 km/h)积分。为了便于分析空气阻力系数与车辆滑行测试速度之间的关系，采用积分中值定理思想，将空气阻力系数的计算结果赋值给滑行速度中值。依照这一计算规则进行计算，可得到表3所示的空气阻力系数计算结果。

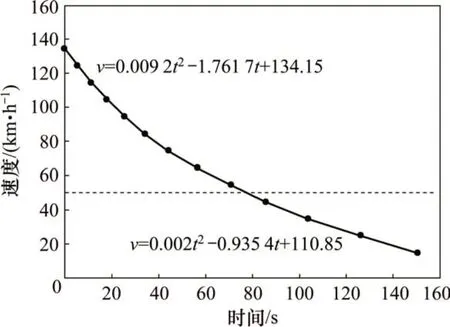
图3 滑行试验结果Fig.3 Results of coast down test

表3 空气阻力系数计算结果Table 3 Calculation results of air resistance coefficient

为了更好地分析空气阻力系数随滑行速度的变化规律，将空气阻力系数与滑行速度之间的关系用曲线表示，如图4所示。

从图4可知：在中低速阶段，随着速度的增加，空气阻力系数也快速增大；在高速阶段，随着速度的持续增加，空气阻力系数反而有轻微下降趋势。运用最小二乘法进行拟合可以得到空气阻力系数与车辆常用车速即滑行车速范围内的关系式：

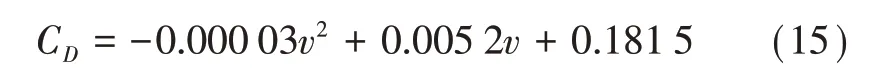
根据空气阻力系数做功(式(6))，对随速度变化的空气阻力系数进行运算，得到的空气阻力如图4所示。从空气阻力的整体变化趋势来看，空气阻力随滑行速度的增大依然是持续增大的，符合汽车运动中空气阻力的变化趋势[20]。

图4 空气阻力系数、空气阻力与车速的关系Fig.4 Relationship among air resistance coefficient,air resistance and vehicle speed

3.3 结果验证

本文中的滑行测试试验设计，参照国Ⅵ标准进行。在道路载荷的计算过程中，国Ⅵ标准综合考虑滑行测试工况，为了确保测试道路载荷的精准性，进一步修正了风速系数和滚动阻力系数；在后续数据的处理中使用滑行时间的调和平均值。国Ⅵ标准中提出数据处理升级手段，使得滑行测试结果更加精准合理，因此，依据国Ⅵ标准的滑行试验道路载荷数据可以当作参考载荷。式(15)依据能量守恒法和滑行试验已完成被测车辆空气阻力系数的数值解析式，且通过图4所示的空气阻力定性地验证了其合理性。为了进一步定量地验证计算所得的空气阻力系数数值解析式的正确性。对试验数据和数值解析式进行进一步处理，利用被测车辆的道路载荷对文中所阐述的思想方法进行验证。将被测车辆的滑行试验数据经过计算且按照国Ⅵ标准修正处理求得的试验道路载荷F2，同时将被测车辆的滑行试验数据代入第1节中所阐述的道路载荷计算式中，利用所计算出的空气阻力系数、滚动阻力系数经验值、传动系阻力已研结果等进行计算，可得出计算道路载荷F1，从而得到试验道路载荷与计算道路载荷的数据表。为了分析计算道路载荷和试验道路载荷之间的关系，利用相对误差((F1-F2)/F2)对误差来衡量计算道路载荷是否能够有效反映滑行试验中的道路载荷，这对于定量检验空气阻力系数计算式的正确性是有必要的。其计算结果如表4所示。

将计算道路载荷与试验道路载荷用曲线拟合，如图5表示。从图5可知：计算道路载荷可以很好地逼近试验道路载荷，且从表4所示的相对误差可以看出：其相对误差较小，可以证明道路载荷的计算式是正确的，从而说明了空气阻力系数的数值计算式是正确的。

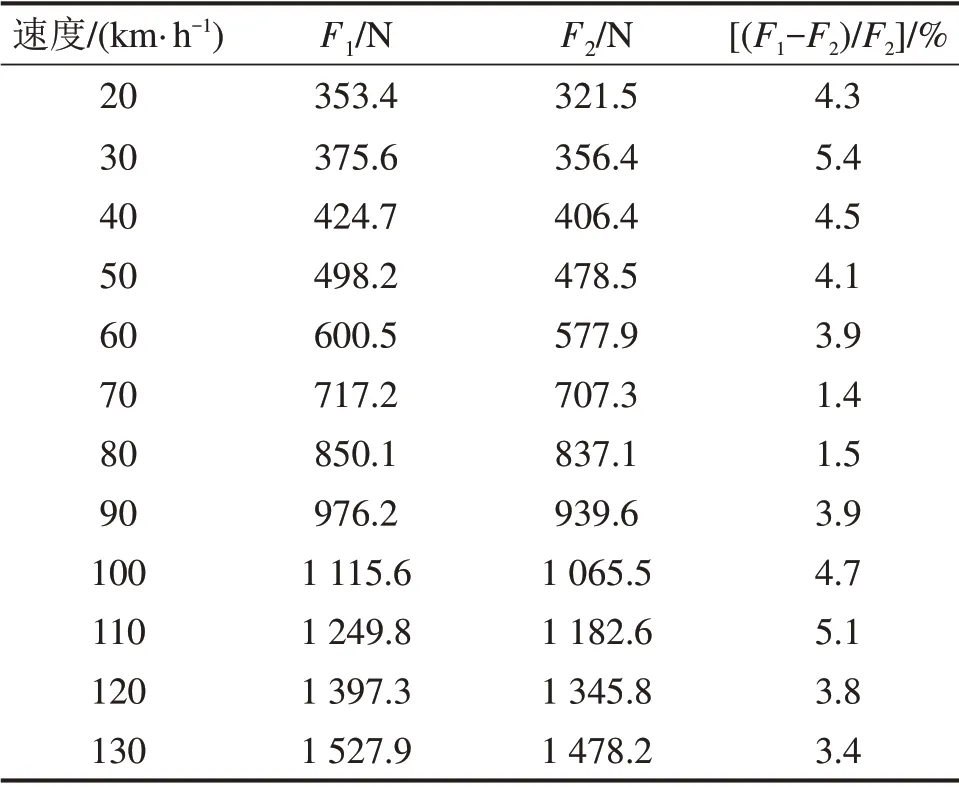
表4 计算道路载荷与试验道路载荷误差分析Table 4 Error analysis of road load between calculation and test

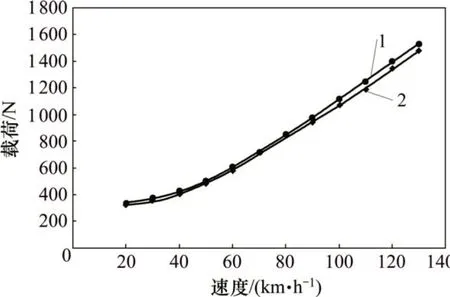
图5 计算道路载荷与试验道路载荷对比Fig.5 Comparison of road load between calculation and test

文中参照国Ⅵ标准进行滑行测试试验，完成空气阻力系数随速度变化的数据推导和验证，综合第3节的数据分析和对所得结果的验证，可得本文的空气阻力系数计算式计算方法是合理、正确的。

4 结论

1) 对被测车辆依照国家最新试验标准进行受力分析，根据滑行车辆的受力情况构建能量守恒方程，从理论角度推导出被测车辆空气阻力系数方程。

2) 利用三段法对被测车辆进行了国Ⅵ标准下的滑行测试，分析采集汽车滑行试验数据，求得被测车辆的空气阻力系数，得到空气阻力系数与滑行车速的关系式，并利用滑行试验对其进行验证，证明空气阻力系数方程的准确性。

3) 本文所提出的基于能量守恒法测试汽车的空气阻力系数方案，可实现高效、准确、经济地检测汽车空气阻力系数，为汽车企业、研究单位对汽车空气阻力的优化设计提供参考。