实验参数对高性能石英纤维摩擦性能的影响

焦亚男， 杨 志， 张世浩

(1. 天津工业大学 纺织科学与工程学院， 天津 300387；2. 天津工业大学 先进纺织复合材料教育部重点实验室， 天津 300387)

在立体织物织造过程中，连续纤维束会发生变形，由此纤维束间产生摩擦损伤，从而影响立体织物的力学性能。纤维束的变形程度与其在立体织物中的取向和分布有很大的关系，研究纤维束在立体织物中的取向和变形对于研究织物中纤维束间的摩擦行为至关重要。从制造高性能纤维束到立体织物织造过程中，纤维束被处理并且必须经历多个机械应力，除张力、扭转和剪切外，还会发生摩擦作用，这些过程对高性能纤维束会造成损伤，甚至导致纤维断裂。纤维束在纺丝和织造[1]过程中的摩擦损伤通常发生在纤维束内部纤维间、纤维束间和纤维束与金属之间。在正交三向织物织造过程中，因摩擦损伤造成的玻璃纤维经纱强力下降30%，法向纱的强力下降50%[2]，因此，研究纤维束的摩擦磨损现象对改善织造工艺条件具有重要意义。

有关纤维束摩擦理论[3-4]的研究大都在20世纪提出，很大一部分源于纺织工业纤维生产过程中单根纤维之间的摩擦、织造过程中纤维束和纤维束以及纤维束和钢筘间的摩擦。早期的研究工作主要集中在聚合物材料和天然材料，如锦纶[5]、粘胶[6]和羊毛[7]。科研人员已对纤维表面摩擦行为和摩擦测量方法作了一些具有重要意义的总结[8]。文献[9]中提出了2种测量纤维束或纤维摩擦的方法：一是用纤维束与纤维束摩擦；二是用纤维束与其他材料摩擦。研究纤维与纤维或纤维束与纤维束之间的摩擦行为，发现其存在2种接触[10]：一是点接触，即纤维束或纤维交叉在一起；二是线性接触，即纤维束或纤维缠绕在一起。目前单根纤维或纤维束与另一种材料之间的摩擦所用的方法多为绞盘法[11]。Cornelissen等[12-13]利用绞盘法研究了温湿度、摩擦方向和法向载荷对芳纶、碳纤维、无碱玻璃纤维摩擦性能的影响，并提出一种接触力学建模方法，为纤维束之间相互接触的摩擦行为提供了理论依据。Allaoui等[14]设计了一种用于分析织物与织物摩擦的实验装置，研究了2个织物层间相对角度、织物成形方式等参数对织物摩擦性能的影响，并提出该设备也可用于研究纤维束与纤维束之间的摩擦性能。Montero等[15]利用设计的一种特殊的实验装置对玻璃纤维平纹织物及其经纬纱之间进行了摩擦实验，研究了载荷和摩擦速度对织物与织物、纤维束与纤维束之间摩擦性能的影响。Michel等[16]通过模拟实验过程研究了碳纤维(经纱)在织造过程中的摩擦损伤现象，分析了摩擦速度、正常载荷和碳纤维类型对纤维束摩擦性能的影响。

立体织物中纤维束的取向对纤维束的变形具有重要影响，而上述文献并未针对纤维束间夹角和纤维束摩擦性能之间的关联性展开研究。为此，本文设计了一种新的测量纤维束或纤维相互之间摩擦性能的方法。该方法利用在摩擦磨损试验机上安装设计好的夹具，通过改变纤维束或纤维在夹具上的相对位置，使纤维束或单根纤维能够以相互正交或一定角度相互接触，从而实现模拟织造过程中经纬纱之间相互交织的状态。本文旨在纤维尺度上研究摩擦角度、摩擦频率和法向载荷对纤维束与纤维束间摩擦性能的影响，讨论并分析实验参数对纤维束间摩擦行为影响或不影响的原因。

1 实验部分

1.1 材料与仪器

石英纤维(线密度为190 tex)，湖北菲利华石英纤维有限公司生产；502瞬间强力胶，深圳市泰顺胶粘剂有限公司。

UMT型摩擦磨损试验机，美国布鲁克公司；夹具，实验室自制；PC-230型数码显微镜，日本Vixen 公司。

1.2 试样制备

实验夹具凹槽及其编号如图1所示。首先，将石英纤维剪成长度为5 cm(上夹具用)和10 cm(下夹具用)的试样，然后让纤维束通过上夹具两端的凹槽，保证凹槽两端纤维束长度相同后，用502瞬间强力胶将纤维束一端黏在上夹具任一测边。最后利用夹子夹住纤维另一端，在保证纤维束在上夹具两侧凹槽内处于伸直的情况下将纤维束另一端黏到夹具上。

图1 自制夹具外形尺寸图

Fig.1 Dimensions of self-made fixtures. (a) Fixture; (b) Schematic diagram of key dimensions of lower fixture

下夹具制作样品过程与上夹具大致相同，在制备90°角摩擦实验时，将纤维束通过下夹具Z(0)槽与Y(0)槽；在制备80°角摩擦时，将纤维束通过Z(-1)(或Z(1))槽与Y(1)(或Y(-1))槽；在制备75°角摩擦时，将纤维束通过Z(-2)(或Z(2))槽与Y(2)(或Y(-2))槽；在制备70°角摩擦时，将纤维束通过Z(-3)(或Z(3))槽与Y(3)(或Y(-3))槽。每组实验制样5件。

1.3 摩擦磨损实验

摩擦磨损的测试方法有很多，材料的摩擦性能可随着摩擦频率、载荷、摩擦速度、温度以及材料属性等因素的变化而变化。实验测试参数为法向载荷(0.3、0.6、0.9、1.2 N)、摩擦频率(0.5、1、1.5、2 Hz)和摩擦角度(70°、75°、80°、90°，纤维束间所夹的锐角)，上下纤维束间摩擦接触距离为20 mm，摩擦时间为5 min。测定不同法向载荷、摩擦频率和摩擦角度对石英纤维表面形貌及摩擦因数的影响。图2示出摩擦时夹具上机的状态。其中左边显示了上下夹具在试验机中的具体位置以及力传感器可移动和探测方向，右边显示了不同摩擦角度下上下纤维束之间接触的真实情况。首先在摩擦磨损试验机上安装好自制夹具，然后在电脑软件上设置好实验参数(摩擦频率、法向载荷、摩擦时间、摩擦方式和摩擦动程)，对纤维束与纤维束进行往复式摩擦测试。

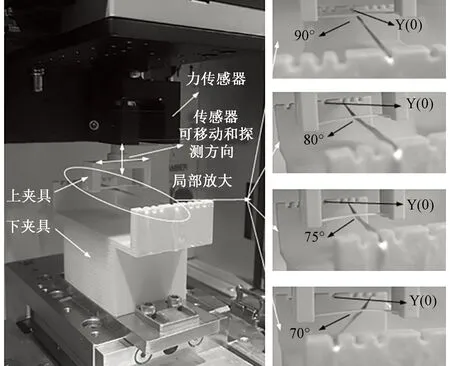
图2 夹具上机状态

Fig.2 Fixture on machine

1.4 实验数据处理

测试结束后，保存并处理所采集到的不同测试参数下摩擦因数和法向载荷随时间变化的数据。采用数码显微镜拍摄摩擦后石英纤维束的表面毛羽，经过数据和图片分析得出测试参数对石英纤维摩擦性能的影响。

2 结果与讨论

2.1 摩擦角度对石英纤维摩擦性能的影响

设定摩擦频率为1 Hz，法向载荷为0.6 N，研究不同的摩擦角度(70°、75°、80°、90°)对石英纤维摩擦性能的影响。在摩擦实验过程中可明显发现，随着摩擦角度的逐渐减小，摩擦接触长度增加，石英纤维磨损程度增加。

图3示出在不同摩擦角度的摩擦磨损实验后石英纤维的摩擦磨损对比。可以看出，不同摩擦角度下材料的表面特征均不相同，石英纤维在90°和80°摩擦时，摩擦区域中间处相比于摩擦边缘较扁平。这是由于在摩擦过程中施加了法向载荷，使得纤维间相互挤压，从而导致纤维束发生挤压变形。随着摩擦角度的减小，石英纤维束的表面越来越粗糙，纤维磨损程度逐渐增加。从微观分析可得，随着摩擦角度的减小，纤维束与纤维束之间的接触面积逐渐增大[17]，由于纤维属于黏弹性体，随着纤维束间接触面积的增加，纤维束间的摩擦阻力增大，从而导致摩擦后纤维束表面断头纤维较多，即纤维磨损程度大，因此，摩擦角度对纤维束与纤维束摩擦中纤维束外观形貌有重要影响。

图3 不同摩擦角度下石英纤维的磨损图

Fig.3 Worn surfaces of quartz fiber at different friction angles

图4示出当摩擦角度分别为70°、75°、80°和90°时石英纤维的摩擦因数随时间的变化曲线。可以看出：在曲线开始阶段，摩擦因数随着时间的延长出现上下波动，波动时长大约为6 s，6 s后随着时间的推移最终达到稳定状态。产生波动的原因为：在摩擦初始阶段，由于石英纤维束之间存在法向载荷，且纤维束中纤维之间存在一定孔隙，这些孔隙在载荷的作用下随着试样的往复循环运动而逐渐减小，从而出现图3中摩擦中间处成扁平状的现象。

图4 不同摩擦角度下石英纤维的摩擦因数

Fig.4 Friction coefficient of quartz fibers at different friction angles

在纤维束中的纤维发生重排并最终达到稳定后，摩擦因数会出现一段时间逐渐减小的过程，这是因为出厂的纤维束均会上浆处理，在纤维重排稳定后的一段时间内，纤维束与纤维束以一定角度进行摩擦，此时，由于纤维上的浆料在摩擦开始时会起到润滑作用[18]，减小了纤维束之间的摩擦阻力，使得摩擦因数在一段时间内降低。最终，当摩擦角度为70°时，摩擦因数最高；75°和80°时摩擦因数次之；当摩擦角度为90°时，摩擦因数最低。为保证数据的精确，取图4中各条曲线上100～300 s之间的数据，求其平均值并将其作为在法向载荷为0.6 N，摩擦频率为1 Hz条件下该摩擦角度的摩擦因数。最终得出当摩擦角度为70°、75°、80°和90°时，摩擦因数分别为0.187 5、0.176 7、0.168 0和0.160 2，其中摩擦角度为70°时的摩擦因数约为90°时的1.2倍，因此，摩擦角度对纤维束间摩擦因数有影响。

图5示出不同摩擦角度下法向载荷随时间的变化曲线。可以看出，摩擦角度为80°和90°时，由于石英纤维束间夹角较大，法向载荷在刚开始摩擦的1 s内发生较小幅度的降低；而摩擦角度为70°与75°时，法向载荷则发生大幅度的降低。在摩擦开始大约1 s后，法向载荷的大小会随着时间的延长出现上下波动且逐渐减小趋势，该波动产生的主要原因是石英纤维束在摩擦过程中其内部纤维相互挤压重排，从而纤维束在相互接触的地方由类似圆形变为扁平；当纤维束中纤维重排达到稳定状态时，法向载荷下降到最底端，此时随着摩擦运动逐渐趋于稳定，法向载荷迅速上升并恢复到初始状态(即0.6 N)，因此，摩擦角度的变化会对实验前期法向载荷的波动产生影响，进而影响摩擦因数。

图5 不同摩擦角度下纤维束之间的法向载荷

Fig.5 Load between tows at different friction angles

2.2 摩擦频率对石英纤维摩擦性能的影响

设定摩擦角度为90°，法向载荷为0.6 N，研究不同摩擦频率(0.5、1.0、1.5、2.0 Hz)对石英纤维摩擦性能的影响。在实验过程中发现，在改变摩擦频率的条件下，石英纤维的磨损噪声无明显增加，磨损程度有所增加，其摩擦磨损对比如图6所示。

图6 不同摩擦频率下石英纤维磨损图

Fig.6 Worn surfaces of quartz fiber at different friction frequencies

从图6(a)可见，在0.5 Hz的摩擦频率下，石英纤维的磨损程度很小，只有少量的断纤维围绕在纤维束周围；由图6(b)、(c)可以看出，随着摩擦频率的增加，石英纤维在摩擦区域变得逐渐稀薄，纤维的磨损程度逐渐变大，磨断的单根纤维聚集在摩擦区域两端；有图6(d)可知，在2.0 Hz的摩擦频率下，摩擦区域的纤维束磨损成扁平状，此外还观察到有大量磨断的单根纤维松散地沿轴向围绕在纤维束周围。由此发现，当摩擦频率为2.0 Hz时，石英纤维的磨损程度最大。经分析可知，随着摩擦频率的增大，纤维单位时间内接触的次数增多，又因为纤维微观表面是凹凸不平的[16]，因此，纤维间的摩擦阻力和纤维磨损程度会随着摩擦频率的增大而增加。因为各单根纤维的强力不同，从而导致处于纤维束外表面的纤维发生断裂且断裂的位置各不相同，这就是图6中看到不同长度的断头纤维围绕在纤维束周围的原因，因此，摩擦频率对纤维束与纤维束摩擦中纤维束表面形貌有影响。

图7示出当摩擦频率分别为0.5、1.0、1.5和2.0 Hz时石英纤维的摩擦因数随时间变化的曲线。可以看出：在曲线开始阶段，摩擦因数随着时间的延长先增加后减小，且处于波动状态，波动时长大约为6 s；6 s后随着时间的推移，摩擦因数先逐渐减小，最后达到稳定状态。随着摩擦频率的增加，单位时间内摩擦次数增多，纤维的重排达到稳定状态的时间更短。随着时间的变化，不同摩擦频率下的摩擦因数曲线最终达到稳定且稳定阶段的曲线相互交叉，保持在同一水平。为保证数据精确度，取100～300 s之间的数据进行分析，得到该阶段4种频率的摩擦因数平均值约为0.169 9，最大值为0.176 2，最小值为0.163 4，差值为0.012 8，可忽略不计，因此，摩擦频率对摩擦因数没有影响。

图7 不同摩擦频率下石英纤维的摩擦因数

Fig.7 Friction coefficient of quartz fibers at different friction frequencies

图8示出不同摩擦频率下法向载荷随时间变化的曲线。可以看出：在6 s前不同摩擦频率条件下法向载荷的波动曲线变化基本一致；在6 s后，纤维重排达到稳定，法向载荷经过大约4 s的稳定后转而急速上升到预设的0.6 N；100 s后不同摩擦频率对应的法向载荷曲线在0.6 N左右相互交叉。曲线相互交叉的现象是由于在纤维束摩擦过程中伴随有纤维断裂，一旦纤维发生断裂，上夹具黏的纤维束持续附加给下夹具上黏的纤维束的法向载荷就会发生变动，法向力传感器所接收到的数据也就会变动，法向载荷曲线就会发生上下交叉的现象，因此，摩擦频率对前期法向载荷没有影响，进而也不影响摩擦因数。

图8 不同摩擦频率下纤维束间的法向载荷

Fig.8 Load between tows at different friction frequencies

2.3 法向载荷对纤维摩擦性能的影响

设定摩擦角度为90°，摩擦频率为1 Hz，研究0.3、0.6、0.9、1.2 N不同法向载荷对石英纤维摩擦性能的影响。在摩擦实验过程中发现，在摩擦过程中，随着法向载荷的增加，摩擦剧烈，石英纤维磨损程度增加，石英纤维材料的表面摩擦磨损对比如图9所示。

图9 不同法向载荷下石英纤维磨损图

Fig.9 Worn surfaces of quartz fiber at different load

由纤维束表面断裂毛羽可知，不同法向载荷下纤维束的表面特征均不相同，且图9(a)～(d)所示纤维束磨损程度逐渐增大，当法向载荷为1.2 N时，石英纤维磨损程度最大。在法向载荷增加的过程中，纤维束磨损程度逐渐增加，纤维束磨损程度与图6相似且比较明显，但相比于图3，纤维束磨损程度相对较小。通过观察分析，随着法向载荷的增加，纤维束磨损程度增加的机制是：增加法向载荷的同时，石英纤维束与纤维束之间的接触面积增加，摩擦界面上纤维与纤维之间的接触力增大，在进行往复摩擦运动时，纤维间接触力较大就会产生较大的摩擦阻力，进而产生更多的纤维断裂，因此，法向载荷对纤维束摩擦的表观形貌有影响。

图10示出当法向载荷分别为0.3、0.6、0.9和1.2 N时石英纤维的摩擦因数随时间的变化曲线。可以看出，在曲线开始阶段，摩擦因数随着时间的延长而出现短暂增加，然后发生6 s的波动，紧接着出现一定程度的下降，最终达到稳定状态。在初始阶段大约1 s时，法向载荷越小，摩擦因数值越大。这说明随着法向载荷的增加，纤维重排达到稳定状态的时间更短，因此，该曲线符合实际情况。为保证数据精确度，取100 ～300 s之间的数据进行分析，从而得出该阶段4种频率的摩擦因数平均值，约为0.175 0，其中最大值为0.179 9，最小值为0.170 0，最大值与最小值之间的差值为0.009 9，可忽略不计，因此，法向载荷对摩擦因数没有影响。

图10 不同法向载荷下石英纤维的摩擦因数

Fig.10 Friction coefficient of quartz fiber under different normal loads

3 结 论

1)石英纤维束之间摩擦角度在70°时，纤维束磨损程度最大，90°时磨损程度最小，摩擦角度对石英纤维束表面形貌有影响；摩擦角度为70°时的摩擦因数为90°时的1.2倍，摩擦角度对摩擦因数有影响，随着摩擦角度的减少，摩擦因数增大。

2)摩擦频率为2.0 Hz时，石英纤维束磨损程度最大，摩擦频率对纤维束表面形貌有影响；不同摩擦频率下纤维束与纤维束之间的摩擦因数值相差0.012 8，摩擦频率对摩擦因数无影响。

3)法向载荷为1.2 N时，石英纤维束磨损程度最大，法向载荷对纤维束表面形貌有影响；不同法向载荷下纤维束与纤维束之间的摩擦因数相差0.009 9，法向载荷对摩擦因数无影响。

综上所述，在一定范围内，摩擦角度、摩擦频率和法向载荷对石英纤维束的表面磨损均有影响，但仅摩擦角度对纤维束与纤维束间的摩擦因数有影响，且随着摩擦角度的减少，摩擦因数增大。在实际织造过程中，应以解决由纤维束的取向在织造过程中发生变形造成的摩擦损伤为主，再考虑减缓织造频率和减小外部载荷来减小立体织物中的摩擦损伤，从而降低立体织物织造过程中造成的力学性能和使用寿命的损失。