基于最小二乘支持向量机的棉针织物活性染料湿蒸染色预测模型

陶开鑫， 俞成丙， 侯颀骜， 吴聪杰， 刘引烽

(上海大学 材料科学与工程学院， 上海 200444)

湿蒸染色是一种短流程的连续加工工艺，将促染剂、碱剂、染料等配制在混合液中，织物经过浸轧后，直接用饱和蒸汽或过饱和蒸汽进行汽蒸，实现快速固色，一般通过浸轧—汽蒸—水洗工艺进行织物的连续染色，可大大缩短工艺流程，适用于活性染料上染棉织物[1-2]。在棉织物活性染料染色过程中，各个染色工艺条件对棉织物染色深度(K/S值)的影响往往是非线性的，尽管已有不少报道将染色模型应用于染色过程，但鲜有较为精确的数学模型[3-4]。最小二乘支持向量机(LS-SVM)[5]建立在结构风险最小化原则基础上，是标准支持向量机的一种扩展，它将标准支持向量机中的不等式约束问题转化为等式约束，且将误差平方和损失函数作为训练集的经验损失，把支持向量机的求解从二次规划问题转化为求解线性方程组，从而提高了收敛速度和精度，也减少了计算的复杂性。它在解决小样本、非线性及高维模式识别中，表现出许多特有的优势，已被广泛地应用于不同领域不同参数的软测量建模中，并在化工、冶金、航空、交通等领域取得了较好的效果[6-8]，但在染色研究中有关应用的报道还较少。

本文用活性染料对棉针织物进行了湿蒸染色研究，基于MatLab R2017b平台，通过对染色效果的分析，运用LS-SVM工具箱进行编程、训练、建模和验证，建立了元明粉和纯碱浓度、汽蒸时间对染色织物K/S值间的数学联系，并对染色织物的K/S值进行了预测。

1 实验部分

1.1 材料与设备

织物：纯棉双罗纹组织漂白织物(纱线线密度为14.58 tex，面密度为180 g/m2，南通新西尔克针织服装有限公司)；染料：雷马素金黄RGB(德司达(上海)贸易有限公司)；试剂：无水纯碱、无水硫酸钠(均为化学纯，国药集团化学试剂有限公司)。

设备：Color I5型台式分光测色仪(美国X-Rite公司)，均匀小轧车(绍兴县威达机械有限公司)，热风定型小样机(绍兴县威达机械有限公司)，微型万能汽蒸机(瑞士 Mathis公司)。

1.2 染色工艺流程

浸轧染料、元明粉和碱液的混合液(染料质量浓度为15 g/L，一定量无水硫酸钠，一定量纯碱；二浸二轧，带液率为60%)→汽蒸(100～102 ℃，饱和蒸汽，一定时间)→冷水洗→热水洗→皂洗(标准皂片质量浓度为3 g/L，浴比为1∶50，90 ℃处理15 min)→热水洗→冷水洗→烘干。

1.3 染色实验方案设计

用活性染料上染棉针织物，采用湿蒸染色工艺，在饱和蒸汽中固色，虽然影响染色织物K/S值的内外界影响因素有很多，但结合湿蒸染色实验的结果，忽略K/S值次要的影响因素，如汽蒸时常压下饱和蒸汽的温度、烘干时的温度、风速和湿度、测量K/S值时光线强度等，选取元明粉质量浓度、纯碱质量浓度和汽蒸时间3个主要影响K/S值因素作为模型输入变量，染色织物K/S值作为模型的输出变量。

1.4 K/S值的测定

使用Color I5型台式分光测色仪对染色后织物进行测定，测试前先用白砖、黑镜和待染漂白织物进行校验，然后在430 nm波长处测试染色试样的K/S值。每个被测染色试样折叠成4层，任意选取试样上8个不同部位进行测试，结果取平均值。

2 结果与讨论

2.1 LS-SVM回归模型的算法

在染色实验研究中，应用LS-SVM建立模型时，如果样本过大，其计算量也迅速增大，计算时间很长。本文选择40组染色样本(l=40)数据作为训练集，即40行4列数据矩阵。建立染色模型使用的LS-SVM的算法[9]主要描述如下：首先选择1个非线性映射φ(xi)，把n维输入数据为x和一维输出数据为y的样本向量[(x1,y1),(x2,y2),,(xl,yl)，xi∈Rn，yi∈R，i=1,2,,l]从原空间映射到高维特征空间。LS-SVM的回归方程如下：

yi=f(xi)=wT·φ(xi)+b

(1)

式中：w为权重向量；常数b为偏置项。LS-SVM的优化问题为

(2)

式中：γ为正则化参数；ξ为误差变量。相比于SVM算法，其约束条件有所不同，变为如下形式：

yi=wT·φ(xi+b+ξi,i=1,2,,l

(3)

即将支持向量机的不等式约束改为等式约束，构造拉格朗日函数L进行求解:

五十年前，那应该是海宁人查良镛大学刚毕业，担任上海《大公报》编辑那会儿，也是他和原配太太杭州人杜治芬结识的时候。揣度大侠年轻时的生活，几乎可以拼接出完整的画面来：一个初入文化行业的愤青，在邻城风光秀美的西湖，红颜做伴，美食好酒傍身，整一个令狐冲式的笑傲江湖。

(4)

式中，αi为拉格朗日乘子。根据Karush-Kuhn-Tucker(KKT)条件，得到如下等式约束条件：

(5)

对于i=1,2,,l，通过式(5)消去w和ξ，得到如下线性系统：

(6)

式中:I为单位矩阵；α为支持向量。

(7)

用Ω表示核矩阵内积，核函数如下：

Ω=φ(xiTφ(xj=K(xi,xj,i,j=1,2,,l

αi和b由式(6)求解，故回归模型为

(8)

上述αi和b具体在MatLab平台中通过应用LS-SVM工具箱编程运行得到，α是一个40行1列的矩阵，即每行数据都成为对模型有贡献的支持向量。

2.2 LS-SVM回归模型的建立过程

首先对40组染色实验结果数据进行预处理。将40行4列的原始数据矩阵分成40行3列的输入变量矩阵和40行1列的输入变量矩阵导入MatLab的工作平台中。为避免因输入与输出变量相差太大，消除不同量纲的影响，需要对原始数据进行预处理，即归一化处理。通过数据归一化，将有量纲的表达式经过变换转化为无量纲的表达式，即成为纯量。如果训练集经过归一化，那么得到的预测数据还要经过反归一化才能得到真实的预测值。归一化处理的方式是调用MatLab平台中自带的多种归一化函数，常用的有mapminmax和mapstd这2种数据标准化处理函数，既可归一化也可反归一化。原始数据也不是一定要经过归一化处理，具体要看模型的预测值与实验值的误差大小，本文建立染色模型时各组染色实验的原始数据均没有经过归一化处理。

最后，调用LS-SVM工具箱中的trainlssvm函数进行编程训练染色模型，再调用simlssvm函数进行编程验证染色模型，即导入预测数据的输入变量(染色条件)得到输出变量(染色织物的K/S值)，再与实验数据进行比较。

2.3 LS-SVM回归模型的确定

雷马素RGB染料属二氟一氯嘧啶基活性染料，具有中等反应活性，较高的固色率，对棉织物湿蒸工艺的适应性较好，因而本文选用雷马素金黄RGB进行湿蒸染色实验。

在tunelssvm函数使用接口中，联用gridsearch和crossvalidatelssvm(交叉验证)2种函数多次编程验证比较，最终选择最佳模型参数为(γ,σ2)=(1 370.355 8，694.450 4)，b=7.436 6，支持向量α见表1。将40组染色实验样本的K/S实验值与用染色模型得到的回归值进行对比，列于表1中。

表1 40组染色样本K/S的实验值和回归值

Tab.1 Experimental values and regression values ofK/Sfor 40 groups of stained samples

实验号实验方案K/S值X1X2X3实验值回归值相对误差/%支持向量α121.437.52907.047.202.27-219.14242.867.52909.058.723.65448.78364.297.529010.4310.390.3849.94485.717.529011.6112.164.74-758.765100.007.529013.6713.372.19410.486107.147.5212014.6414.730.61-128.827125.007.5212016.9316.572.13491.398150.007.5212018.5718.911.83-461.329175.007.5212021.0220.850.81234.9710125.003.7615013.7813.890.80-157.3811125.009.4015017.9617.472.73677.2812125.0015.0415016.9216.820.59142.8913125.0020.6815017.2917.280.0617.3514125.0026.3215018.5618.560.00-5.471575.0015.049012.9713.020.39-61.721675.0015.0412012.4012.310.73125.051775.0015.0415014.1914.240.35-65.371875.0015.0418013.9513.791.15225.421975.0015.0421014.3114.702.73-535.142075.0015.0424015.6215.610.0618.8521150.003.7618019.6219.570.2566.1622150.009.4018019.2419.170.3690.1623150.0015.0418019.5819.460.61160.7224150.0020.6818019.7319.860.66-176.0225150.0026.3218020.0319.990.2060.8126125.007.5221015.5815.500.51111.9427125.0015.0421020.1619.453.52970.5428175.007.5221015.2115.280.46-102.5229175.0015.0421018.3718.701.80-453.1130100.0011.289014.7014.610.61129.4531100.0011.2812013.2913.461.28-239.2832100.0011.2815015.4515.430.1320.9433100.0011.2818013.5713.862.14-397.3934100.0011.2821015.1915.210.13-21.5735100.0011.2824014.5014.510.07-13.203650.0011.2815010.3910.211.73242.153775.0011.2815012.6412.972.61-450.5038125.0011.2815016.8017.423.69-846.2339150.0011.2815019.6318.764.431187.4640175.0011.2815018.8019.383.09-789.78

注：X1代表元明粉质量浓度/(g·L-1)，X2代表纯碱质量浓度/(g·L-1)，X3代表汽蒸时间/s。相对误差取绝对值。下同。

从表1可看出，虽然数据两端相对误差较大，但中间较小，且平均相对误差只有1.41%，调用corrcoef函数得到染色实验值和回归值的相关系数R为0.995 8(大于0.9)，统计量概率P值远远小于0.01，表明该模型的拟合度较高。

2.4 不同参数模型拟合与预测性能的分析

在用LS-SVM方法建立模型时，存在若干组参数(γ,σ2)可使模型均具有较好回归性，但用所得的回归模型进行数据推广时，往往在导入输入变量后，预测值的准确性存在很大差异，需要从中找出最佳的参数(γ,σ2)。

针对40组实验染色数据矩阵，联用gridsearch和crossvalidatelssvm这2种函数寻找得到5组相对最优的参数(γ,σ2)，分别取值为A=(1 606.840 8，547.042 6)、B=(1 370.355 8，694.450 4)、C=(92.672，2.209 2)、D=(62.129 9，3.475 2)和E=(35.094 1，2.903 7)。然后将上述5组参数(γ,σ2)分别代入模型，进行建模并拟合回归，结果见表2。

表2 模型拟合回归性能对比

Tab.2 Comparison of model fitting regression performance

(γ,σ2)均方误差均方根误差R值P值平均相对误差/%A0.069 40.263 40.996 8 <0.000 11.17B0.091 70.302 80.995 8<0.000 11.41C0.001 10.033 20.999 9<0.000 10.20D0.002 10.045 80.999 9<0.000 10.28E0.006 80.082 50.999 9<0.000 10.49

由表2可知，5组参数建立染色模型得到的回归值和染色实验值的R值均大于0.99，P值均小于0.000 1，说明5组参数建立的染色回归模型均有很好的拟合回归性能。

选择合理的5组染色实验测试数据，即5行3列的输入变量矩阵，分别代入由表2中5组参数(γ,σ2)建立的5个染色模型中，预测棉针织物活性染料用湿蒸染色后织物的K/S值，并和实验得到的K/S值作比较，结果见表3。可以看出，A组参数(1 606.840 8，547.042 6)建立的回归模型，其最大相对误差为1.55%，最小相对误差为0.65%，平均相对误差为1.18%；B组参数(1 370.355 8，694.450 4)建立的回归模型，其最大相对误差为1.31%，最小相对误差为0.27%，平均相对误差为0.84%；而C、D、和E3组参数建立的回归模型，最大相对误差均大于90%，最小相对误差均大于0.80%，平均相对误差均大于28%。只有选择A组或B组参数时，染色模型回归预测性能才是相对较优的，且B组参数建立的染色模型预测性能要优于A组参数，故本文选择B组参数(γ,σ2)=(1 370.355 8，694.450 4)建立染色回归模型，而其他3组参数模型表现出较差的推广能力和过学习现象，虽有较好的拟合数据，但染色实验的预测效果较差。

表3 模型预测性能对比

Tab.3 Comparison of model prediction performance

实验号实验方案K/S值X1X2X3实验值预测值相对误差/%(γ,σ2)135.716.771087.918.0331.55278.579.0214012.8312.6551.36392.8615.7917014.9414.8100.874128.5713.5420517.1017.2120.655157.1422.568219.4119.6951.47A135.716.771087.918.0141.31278.579.0214012.8312.6741.22392.8615.7917014.9414.9000.274128.5713.5420517.1017.1780.465157.1422.568219.4119.5970.96B135.716.771087.9115.18391.95278.579.0214012.8315.18318.34392.8615.7917014.9415.1831.634128.5713.5420517.1015.19711.135157.1422.568219.4115.18321.78C135.716.771087.9115.06890.49278.579.0214012.8315.06817.44392.8615.7917014.9415.0680.864128.5713.5420517.1015.17511.265157.1422.568219.4115.06822.37D135.716.771087.9115.21592.35278.579.0214012.8315.21518.59392.8615.7917014.9415.2151.844128.5713.5420517.1015.26510.735157.1422.568219.4115.21521.61E

2.5 模型预测性能的验证

在一定工艺范围内，再次任选5组染色工艺条件代入B组参数染色模型进行预测验证，结果见表4。可以看出，实验得到的5组染色织物的K/S值均与模型预测的K/S值接近，B组参数染色模型得到的预测值和实验值的相关系数R为0.999 6，统计量概率P小于0.000 1，最大误差为1.61%，最小误差为0.10%，平均相对误差为0.99%。

表4K/S实验值和K/S预测值的对比

Tab.4 Comparison of experimentalK/Svaluesand predictedK/Svalues

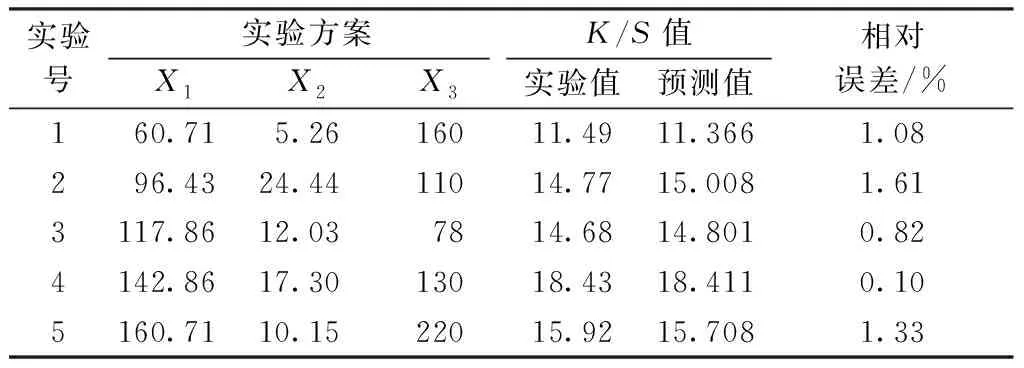
实验号实验方案K/S值X1X2X3实验值预测值相对误差/%160.715.2616011.4911.3661.08296.4324.4411014.7715.0081.613117.8612.037814.6814.8010.824142.8617.3013018.4318.4110.105160.7110.1522015.9215.7081.33

综上分析，再次验证了染色模型参数取值为B组参数(γ,σ2)=(1 370.355 8，694.450 4)时，染色模型在一定工艺条件范围内可较精准地预测染色棉针织物的K/S值。染色实验预测结果验证了该模型具有很高精确度，可适用于在棉针织物活性染料湿蒸染色工艺中对染色织物K/S值进行预测。

3 结 论

本文在MatLab平台中应用LS-SVM工具箱，建立了棉针织物活性染料湿蒸染色的多因素影响K/S值模型，该模型具有很高的拟合度，染色织物的K/S回归值和实验值的相关系数R为0.995 8，统计量概率P远小于0.01。同时染色验证实验结果表明，该染色模型对棉针织物采用湿蒸染色工艺进行活性染料染色，具有很好的K/S值预测能力，可用于活性染料对棉织物湿蒸染色工艺的预测和优化。