创设问题情境 引导学生探究——处理多面体外接球问题的常用方法和技巧

广东

球是立体几何的重要内容.多面体的外接球问题是培养学生直观想象、数学抽象、逻辑推理和数学运算等核心素养的重要载体.因此，在近几年的高考、自主招生和数学竞赛中，频频出现了与多面体相关的外接球的问题.这类问题由于不易画图而变得抽象难解，解决问题的关键在于确定球心的位置.本文从课堂教学出发,立足基础知识和基本技能,谈谈这类问题的处理方法和技巧.

一、基本知识

定义：空间中，若一个定点到一个几何体的各顶点的距离都相等，则这个定点就是该几何体的外接球的球心.

性质：球心与截面圆圆心的连线垂直于截面圆.

根据上述的定义与性质，可以确定简单多面体外接球的球心的位置有如下结论:

1.长方体的外接球的球心是该长方体的体对角线的中点,半径为体对角线长的一半.

2.直三棱柱(侧棱垂直于底面的三棱柱)的外接球的球心是该直三棱柱上下底面三角形外心的连线的中点,半径可在以球心、底面圆心和底面三角形的一个顶点为顶点组成的直角三角形中求解.

3.正棱锥的外接球球心在该正棱锥的高上，半径可在以球心、底面中心和底面正多边形的一个顶点为顶点组成的直角三角形中求解.

4.若棱锥的顶点可构成共斜边的直角三角形，则公共斜边的中点就是其外接球的球心.

5.过几何体其中两个面(外心较易找到)的外心分别作这两个面的垂线，垂线的交点即为球心.

当画球O的内接四面体的底面△ABC时，通常将一点A画在边界上，另外两点B,C放置于截面圆O1的圆弧其他位置.当△ABC分别为任意三角形、等边三角形和直角三角形时的情形及几何量内在基本关系如图1，图2，图3(其中，O1为△ABC的外心，OO1⊥平面ABC，OO1=d,r是圆O1的半径，球O的半径为R,R2=d2+r2).

图1.

图2.

图3

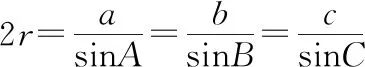
二、基本方法

1.定义找心

在几何体中，可以通过以下途径找到到各顶点距离相等的点.

1.1若四面体两个面是公共斜边的直角三角形，则球心为斜边中点

( )

所以PA2+PC2=AC2，故△APC为直角三角形.

取△APC与△ABC的公共斜边AC的中点O，则有AO=PO=CO=BO，故点O为三棱锥P-ABC外接球的球心，外接球的半径为AO=2，球的表面积为4πAO2=16π，故选D.

1.2直三棱柱的外接球的球心在该直三棱柱的上下底面三角形外心的连线的中点处

【例2】(2010·课程标准卷理·10)设三棱柱的侧棱垂直于底面，所有棱的长都为a，顶点都在一个球面上，则该球的表面积为

( )

解析：设O1,O2分别是正三角形A1B1C1和正三角形ABC的中心，因为三棱柱A1B1C1-ABC是正三棱柱，所以其外接球的球心O是O1O2的中点，如图，于是其外接球的半径为

2.垂线找心

如图，选取球面上的任意两个截面圆(不平行),过其圆心作两个圆面的垂线,这两条垂线的交点即为球心.这两个截面圆即多面体的两个面的外接圆,因此可在过多面体面的外心且垂直于该面的直线上寻找多面体外接球的球心.

为便于找到球心，常选择多面体中具有特殊形状的面(如直角三角形、等腰三角形或正方形等)进行分析.

2.1多面体有一个面为直角三角形

若多面体有一个面为直角三角形，则在过斜边中点且垂直于该直角三角形所在平面的直线上寻找球心.

( )

A.1 B.2

C.4 D.8

解析：如图，因为CD2=BC2+BD2,所以∠CBD=90°，取CD的中点H，则CH=BH=4，球心O1在过H且垂直底面BCD的直线上.

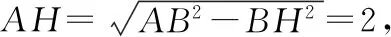
解得O1A=5,O1H=3.

显然当球O2与平面BCD相切且在平面BCD下方与球O1内切时直径最大，最大值为O1H与球O1半径之和，故球O2直径的最大值为8.

2.2多面体有一个面为等边三角形

若多面体有一个面为等边三角形，则在过等边三角形的中心且垂直于该等边三角形所在平面的直线上找球心.

【例4】在四面体ABCD中，有一条棱长为3，其余五条棱长皆为2，则其外接球的半径为________.

解法1：不妨设BC=3，通过分析过等腰△ABC的外心且垂直于该等腰三角形所在平面的直线寻找球心.

AB=AC=AD=BD=CD=2.过点D作DH⊥平面ABC，垂足为H.则由AD=BD=CD，易知AH=BH=CH，则点H是△ABC的外心，从而DH上任意一点到点A,B,C的距离都相等.取BC的中点E，连接AE,DE，则由AB=AC可得AE为BC的中垂线，从而点H在AE上.取AD的中点F，连接EF，则由图形的对称性易知AE=DE,EF为AD的中垂线.设DH∩EF=O，则有OA=OD.

综上，可知点O到点A,B,C,D的距离相等，则点O就是四面体ABCD的外接球的球心.

解法2：不妨设AB=3，通过分析过等边△BCD和△ACD的外心且分别垂直于它们所在平面的两垂线寻找球心.

AC=AD=BC=BD=CD=2.取CD的中点E，连接AE，BE，可得AE⊥CD，BE⊥CD，则由△BCD和△ACD都是等边三角形可知它们的中心M,N分别在BE，AE上，且BM=2ME，AN=2NE.

在△ABE内，过点M作BE的垂线，过点N作AE的垂线，设其交点为O.连接OB,OE，因为AE⊥CD，BE⊥CD，则CD⊥平面ABE，进而CD⊥OM，CD⊥ON.结合OM⊥BE，ON⊥AE，可知OM⊥平面BCD，ON⊥平面ACD.由此再结合BM=CM=DM=AN=CN=DN，可知点O到点A,B,C,D的距离相等，故点O就是四面体ABCD的外接球的球心.

2.3多面体有一个面为矩形

若多面体有一个面为矩形，则在过矩形的中心且垂直于该矩形所在平面的直线上找球心.

【例5】四棱锥P-ABCD的三视图如图所示，则该四棱锥外接球的表面积为

( )

正视图

侧视图

俯视图

解析：根据三视图还原几何体直观图，如图所示.在四棱锥P-ABCD中，平面PAD⊥平面ABCD，△PAD为等腰三角形，PA=PD=3,AD=4，四边形为矩形，CD=2.过△PAD的外心F作平面PAD的垂线，过矩形ABCD的中心H作平面ABCD的垂线，两垂线交于一点O，点O即为四棱锥外接球的球心.

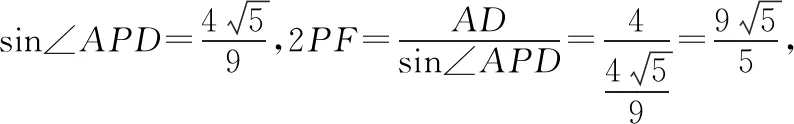
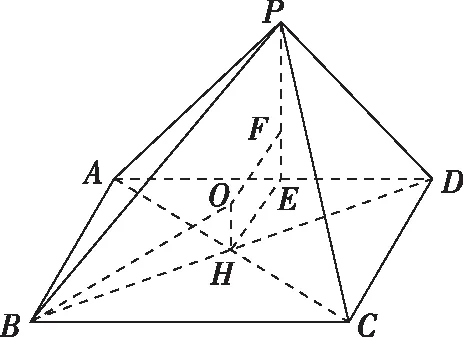
2.4多面体中有二面角模型

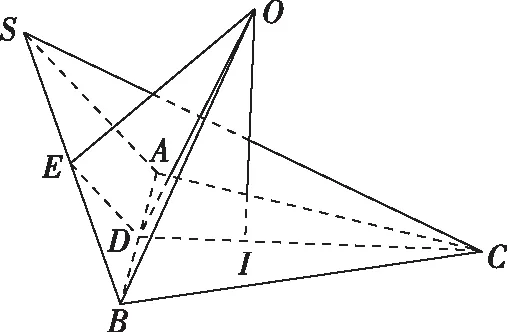
若多面体涉及二面角大小，设过二面角的两个半平面所在三角形外心且垂直所在面的直线为l1，l2，则球心为l1与l2的交点.

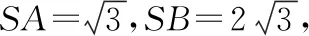
三棱锥S-ABC外接球的球心是平面SAB过点E且垂直于该平面的直线与平面ABC过点I且垂直于该平面的直线的交点O.

在平面四边形OEDI中，∠OED=∠OID=90°,DE=DI,∠EDI=120°,所以Rt△ODI≌Rt△ODE.

3.补形找心

对某些特殊多面体，可通过构造直三棱柱和长方体等几何体，使多面体的顶点为直三棱柱或长方体的顶点，将多面体“镶嵌”在直三棱柱或长方体内，借助直三棱柱或长方体外接球的球心寻找所研究多面体的球心.

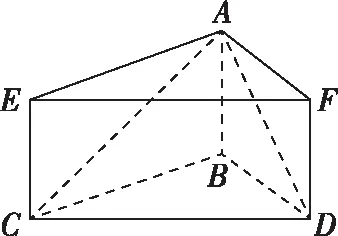
3.1侧棱垂直于底面的棱锥补成直棱柱

解析：由题意，可得AB2+BC2=22+32=13=AC2，

所以AB⊥BC.同理，AB⊥BD.

过点C作CE∥AB,且CE=AB，过点D作DF∥AB,且DF=AB，连接AE,EF,AF，则易知三棱柱AEF-BCD是正三棱柱，则四面体ABCD的外接球与正三棱柱的外接球相同，其球心在该正三棱柱上下底面中心连线的中点处，容易求得球的半径为

故外接球的表面积为4π×22=16π.

3.2三条棱两两垂直的四面体补成长方体

3.2.1“墙角”型

三条棱两两垂直且共顶点：如果三棱锥A-BCD中，过点A的三条棱两两互相垂直，即AB⊥AC,AD⊥AC,AD⊥AB，则可构造以AB,AC,AD分别为长、宽、高的长方体.

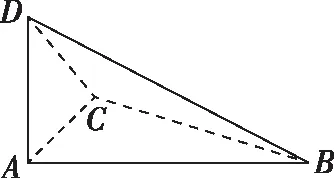
解析：因为PA,PB,PC两两互相垂直，故正三棱锥P-ABC的外接球即是以PA,PB,PC为棱的正方体的外接球，球心是在该正方体的体对角线的交点处，如图，易证OP⊥平面ABC，所以球心O到截面ABC的距离即为球的半径R减去正三棱锥P-ABC的高.设PA=a,则(2R)2=3a2，所以a=2.

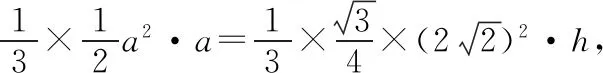
3.2.2“直角+垂线”型

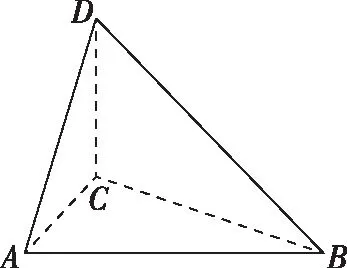
三条棱两两垂直且不共顶点：如果三棱锥D-ABC中，DC⊥平面ABC,∠BAC=90°，则可构造以底面ABC的两条直角边AB,AC和垂线CD分别为长、宽、高的长方体,长方体的体对角线的中点即为球心.

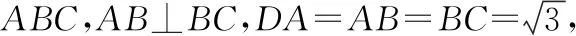
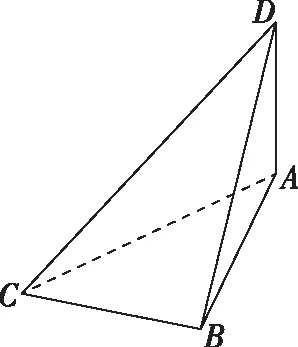
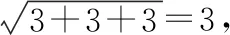
3.2.3 “对棱”相等型

若四面体三组对棱相等，则可构造以三组对棱为六个面的对角线的长方体.

特别地，当AD=BC=AB=CD=AC=BD时(即四面体DABC为正四面体)，长方体就变成了正方体.

4.坐标找心

通过建立空间直角坐标系，利用球心到四个顶点的距离相等求出球心坐标.

设球心O(x,y,z)，由OA=OB=OC=OD可得