提高思维品质，发展直观想象

甘肃

直观想象是六大数学核心素养之一，方法主要有以下几种：

1.利用图形描述数学问题：借助几何直观和空间想象可以把复杂的数学问题变得简明、形象，有助于探索问题的思路，预测解答结果，这在数学学习中发挥着重要作用；

2.利用图形理解数学问题：数学问题的抽象性使得理解数学问题变得困难，通过将数学问题以图形的形式展现出来，形成直观形象的变量关系，更有助于数学问题的理解；

3.利用图形探索解决数学问题：代数问题的求解需要有严格的逻辑思路,若借助图形辅助分析，将代数问题几何化，就会使得逻辑推理变得更自然、更有活力；

4.构建数学问题的直观模型：在数学实际问题解决过程中,建立问题的几何模型，使得问题清晰化、结构化.

高中数学教学的一个主要手段就是利用图象解决有关数学问题,不同的题型有不同的特点,能否应用图形辅助解题,如何应用图形辅助解题都是需要在实际情境中具体分析的.另外有些问题的解题思路就是以图形为基础的,故能借助图形对常见的经典题型流畅解答是十分必要的，下面笔者就分类例谈不同题型的解答策略.

1.数形结合，形象直观

例1.已知方程sinx-lgx=0,求方程根的个数.

分析：方程sinx-lgx=0⟹sinx=lgx，即方程sinx-lgx=0根的个数等于函数y=sinx与y=lgx图象的交点个数.

由图可知函数y=lgx经过点(1,0)和A(10,1),通过观察可知，两图象的交点个数是3个,即方程sinx-lgx=0根的个数是3个.

反思：此题主要考查方程的根与两函数图象交点，常见的解答手段都是作图分析，但在作图过程中要注意两函数图象的相对位置关系.

2.以静制动，简单有效

例2.(2014·全国卷Ⅱ理·16)设点M(x0,1),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°，则x0的取值范围是________.

分析：此题要准确理解“存在”的含义.有两个动点M和N.故需要将点M(x0,1)看成是直线y=1上的点,再来研究N.

(1)当点M在圆上,即M(0,1)时,存在点N(1,0),使得∠OMN=45°.

(2)当点M不在圆上时,过点M做圆的切线，切点为P(0,1),此时∠OMN的最大角为∠OMP.如图1∠OM1P=45°,∠OM2P=45°.

①当点M在线段M1M2上时，∠OMP≥45°,故存在点N使得∠OMN=45°,如图1；

②当点M在线段M1M2外时，∠OMP<45°,故不存在点N使得∠OMN=45°,如图2.

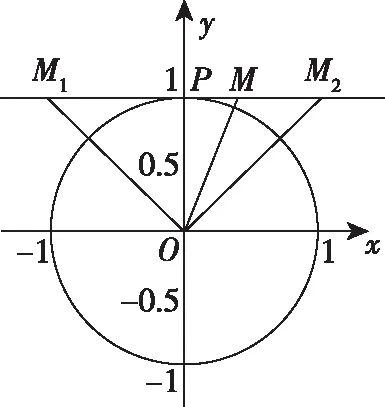
图1

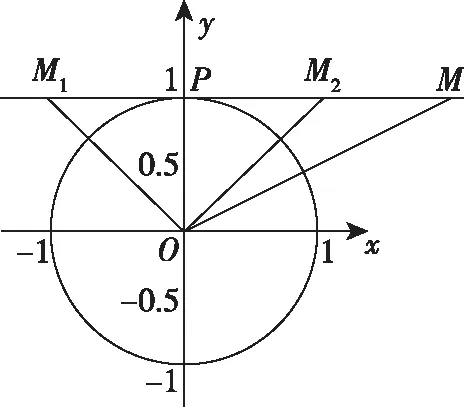
图2

综上可得：x0∈[-1,1].

反思：此题主要考查平面解析几何中圆的相关知识,借助圆的几何图形，将点M几何化，从而能够更清晰的呈现变量之间的关系，这也是解析几何的常用方法.

3.洛必达辅助作图，高效引领思维

分析：y=ax+a,x<0关于原点对称的函数为：y=ax-a,x>0.由于f(x)图象上有且仅有两对点关于原点对称，所以y=ax-a,x>0的图象与y=xlnx,x>0的图象有且仅有两个交点.

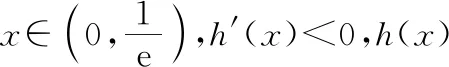
所以h(x)的图象为图3或图4.

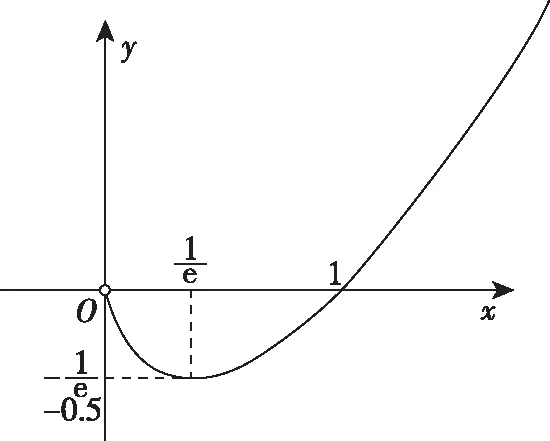
图3

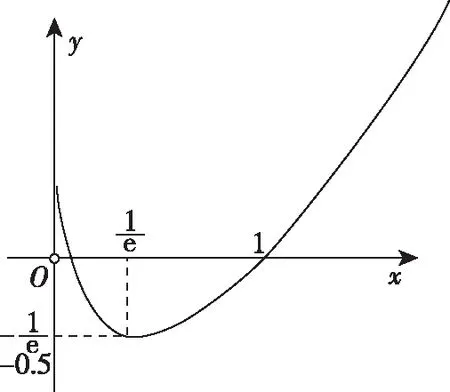
图4

图象到底是图3还是图4，具体分析要看当x→0时，xlnx的极限值.

h(x)=xlnx在x=1处的切线方程为：y=x-1,故有：

当a=1时，y=a(x-1)图象与y=xlnx的图象相切；

当a>1时，y=a(x-1)图象与y=xlnx的图象有两个交点，如图5；

当a<1时，y=a(x-1)图象与y=xlnx的图象也有两个交点，如图6.

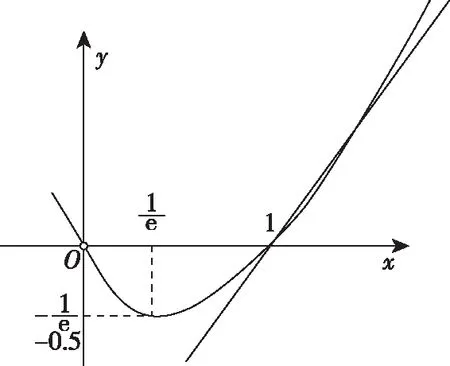
图5

图6

综上可得：a∈(0,1)∪(1,+∞).

反思：此题是应用洛必达法则辅助作图的经典例题,洛必达法则能帮助确定函数图象,在此例题中,根据函数的单调性是无法确定相对准确的函数图象的，只有借助洛必达法则才可以确定.

4.多交点问题注意临界状态

例4.已知f(x)=x2-lnx与g(x)=ax的图象恒有两个交点,求实数a的取值范围.

分析：重点研究y=f(x)与y=g(x)图象只有一个交点的情况,再由此扩展即可.

即当a=1时，两函数图象只有一个交点，如图7；当a>1时，两函数图象有两个交点，如图8.

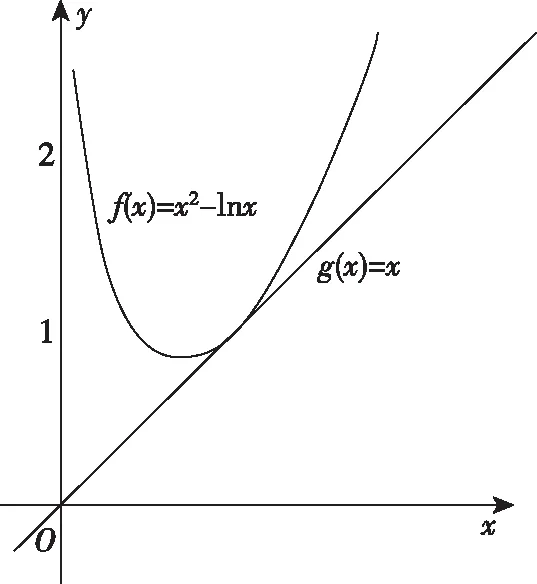
图7

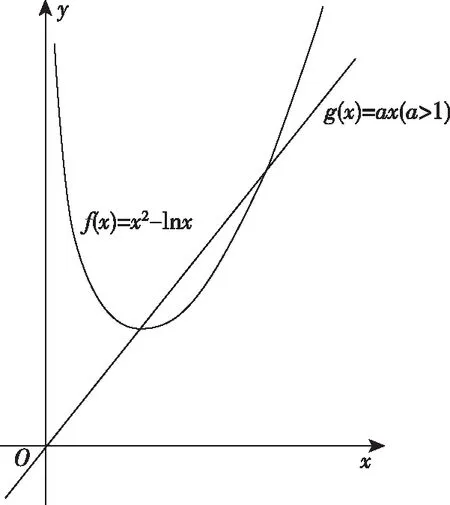
图8

综上可知：a∈(1,+∞).

反思：解决恒成立问题的常用手段是分离参数法,但是有些恒成立问题利用图象解答更简单明了,能起到事半功倍的效果，特别是涉及多交点的问题,利用两函数图象相切的临界情况解题能起到画龙点睛的效果.

5.观察结构，类比联想

例5.定义在[1,+∞)上的函数f(x)满足：(1)f(2x)=2f(x)；(2)当2≤x≤4时，f(x)=1-|x-3|.则g(x)=f(x)-2在区间[1,28]上的零点个数为________.

分析：f(x)=1-|x-3|在区间[2,4]上是确定的函数,而f(x)在[1,+∞)上满足f(2x)=2f(x),对其进行伸缩变换，从而得到f(x)在[1,+∞)上的图象,根据图象可以确定y=g(x)在区间[1,28]上的零点个数.

解题的关键是理解伸缩变换的特点及伸缩的方向,由f(2x)=2f(x)可以得到：

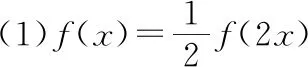
先画出y=f(x)在区间[2,4]的图象，如图9，利用(1)、(2)的变换方式将f(x)分别向左、右作伸缩变换可得y=f(x)在区间[1,28]的图象，如图10.

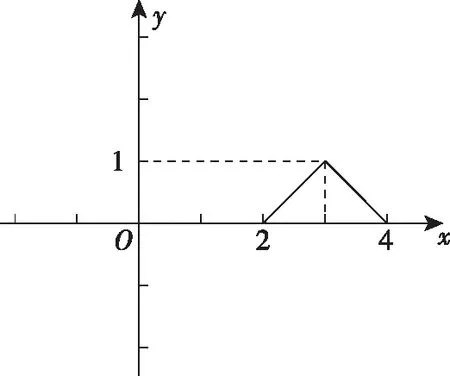
图9

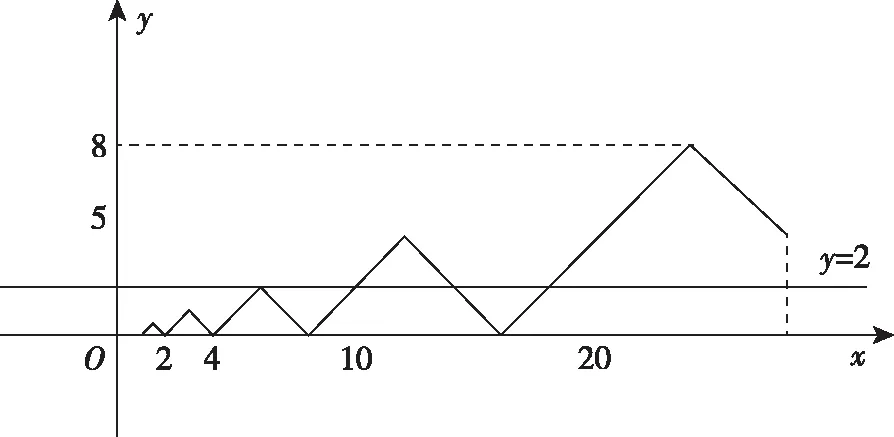
图10

所以y=g(x)在区间[1,28]上的零点个数为y=f(x)的图象与直线y=2的交点个数,由图可知y=g(x)在区间[1,28]上的零点个数为4个.

反思：此题的关键是从几何的角度理解f(2x)=2f(x),结合周期性的特点及图象伸缩变换的特点，把代数式通过图象展现出来.

6.熟练三次函数的图象,从图形中发现问题解决方案

例6.已知函数f(x)=ax3-3x2,若函数g(x)=f(x)+f′(x),x∈[0,2]在x=0处取得最大值.求实数a的取值范围.

分析：已知f(x)=ax3-3x2,则f′(x)=3ax2-6x,即g(x)=ax3-3x2+3ax2-6x，所以g′(x)=3ax2-6x+6ax-6,要利用y=g(x)在x=0处取得最大值，就需要判断g(x)的单调区间I(特别是递减区间)，进一步判断区间I与区间[0,2]的关系，从而得出结论.

然而求解y=g′(x)的零点需要求3ax2-6x+6ax-6=0的根，比较复杂，因此这种纯代数式的解答思路是走不通的，需要借助三次函数的图象特点分析y=g(x)的图象在x=0处的特点.

借图分析，理清思路：

(1)当a=0时,g(x)=-3x2-6x在区间[0,2]上单调递减,有g(x)max=g(0)=0,满足题意，故a=0成立.

(2)当a≠0时,g(x)=ax3-3x2+3ax2-6x=ax2(x+3)-3x(x+2),g(0)=0,g′(0)=-6,即y=g(x)的图象过点(0,0),且y=g(x)在(0,0)处的切线函数单调递减,因此y=g(x)的图象大致为：

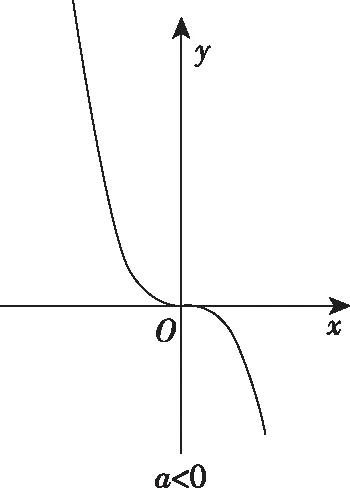
反思：三次函数是很重要的一类函数,根据三次项系数的正负画出函数图象的示意图,进而解决相关问题.