基于Matlab 的扇形环板轴向压缩变形的偏微分方程数值求解∗

潘莉英 曹 岩

（1.陕西省宝鸡教育学院数学系 宝鸡 721004）（2.西安工业大学机电学院 西安 710021）

1 引言

薄板是工程结构中的一种常用构件，它是由两个平行面和垂直于它们的柱面所围成的物体，几何特征是其高度远小于底面尺寸。在纵向载荷和横向载荷共同联合作用时，由于板很薄，假定只发生在平行于中面的应力，且这些应力沿板的厚度是均匀的，此时微分平衡控制方程中不计挠度的非线性项，且没有垂直于板面的载荷q（x，y）=0，得下式［1～6］:

图1 纵向载荷和横向载荷共同联合作用下薄板的力学模型

此式即为直角坐标系中复杂弯曲时的微分平衡控制方程。因此直角坐标系中矩形板在纵向和横向载荷联合作用下失稳的临界载荷的确定只需求解式（1）即可。但是式（1）的严格求解是有困难的，当边界条件比较复杂、或者矩形板有不规则的几何形状，比如扇形板［7］。此时上式Px，Py，Pxy不再是常数，这样常系数微分方程（1）将变为变系数偏微分方程，从而导致无法获得该方程的解析解［8～11］。

2 扇形环板挠曲数学模型的建立

在定解条件下（初始条件及边界条件），求解变系数偏微分方程，针对面内弯曲件的几何形状，可利用扇形环板的小挠度问题近似。那么既满足薄板小挠度的控制方程，又满足某一问题边界条件的挠度函数，就是该问题的解。在板所应当满足的各种条件中（控制微分方程及边界条件），可以根据问题的具体情况，先找出能满足其中一部分条件的挠度函数，其中留有待定系数（或函数），然后令其满足（大多数情况下是近似满足）余下的条件，以决定这些待定常数。如果能精确满足余下的条件，则得到精确解，否则为近似解［12～16］。

2.1 扇形环板小挠度弯曲的数学模型的建立

设有扇形环板如图2所示，中心角为θ0，k=π/θ0（k ∊Z+），因此 θ0≤π ；内圆半径 a ，外圆半径 b，板的直线边简支，而弧边的支座可由边界条件最后决定。以该板的一个直线边为柱坐标的极轴基线，均布载荷P 均匀作用于该扇形环板面，因板服从D(∇4w)=p(r,θ)，故设挠曲曲面方程为式（2）。

图2 扇形环板小挠度弯曲的几何模型

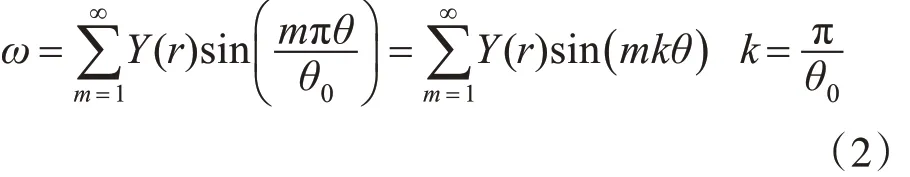
把式（2）代入下式（3），得式（4）。

把 p 化为三角级数，得

代入式（4），得

则式（6）的通解是如下:

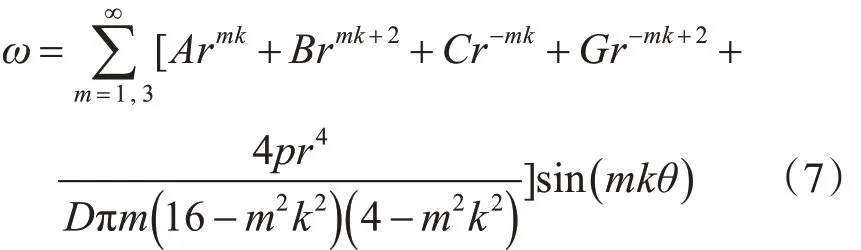
该式含4 个待定系数A，B，C，G 根据弧形边上的4个边界条件决定。当边界条件确定时，则A，B，C，G可计算获得，则扇形环板的挠曲形式也就确定。

2.2 扇形环板小挠度弯曲的边界条件的数学处理方法

扇形环板的边界条件为:对r=a 为简支边，该边无挠度，且该边力矩为零。则有(ω)r=a=0(Mr)r=a=0。对r=a 为固定边，虽然该边受力的情况不明，但位移是可以确定的，即该边无挠度，且中面法线没有任何方向之转角，则有(ω)r=a=0 ，=0。对r=a 为自由边，该边的位移情况不明，但确知什么力都不作用在此边上，则有

3 不同边界条件下扇形环板的挠曲面形貌

3.1 内圆固支外圆简支扇形环板挠曲问题的求解

设r=a为固支，r=b为简支，则有

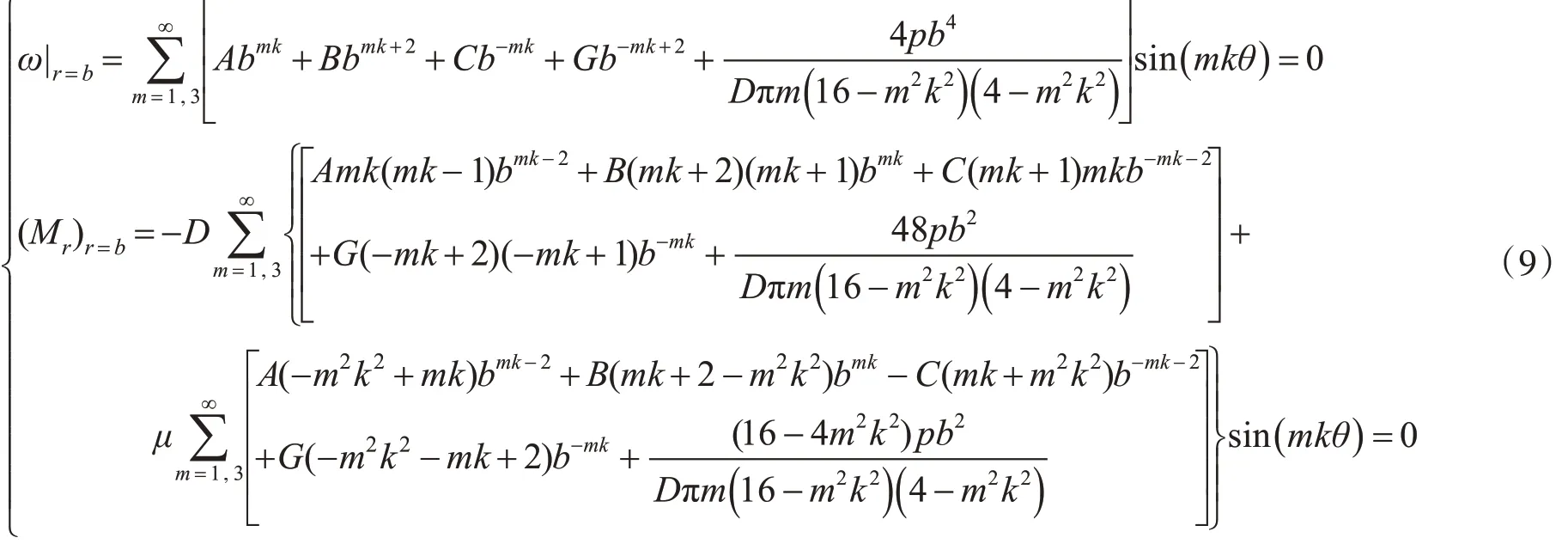
对上面4个方程联立求解，得出A，B，C，G 的显式解的表达式，根据几何参数和物理参数a=20，b=50，m=1，k=1.5，u=0.3，D=100，p=10000000。取 A5，B5，C5，G5，A7，B7，C7，G7，A9，B9，C9，G9共计 19 个值，代入通解表达式（7），取前5 项，在Matlab 中作挠度曲面图如图3所示。

图3 当r=a固支，r=b简支时扇形环板挠度曲面图

3.2 其它8种边界条件下的解

图4 当r=a简支，r=b固支时扇形环板挠度曲面

图5 当r=a简支，r=b自由时扇形环板挠度曲面

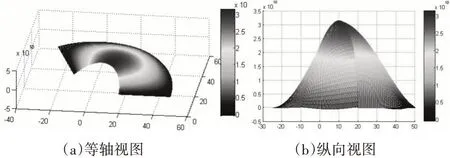
图6 当r=a自由，r=b简支时扇形环板挠度曲面

图7 当r=a简支，r=b简支时扇形环板挠度曲面

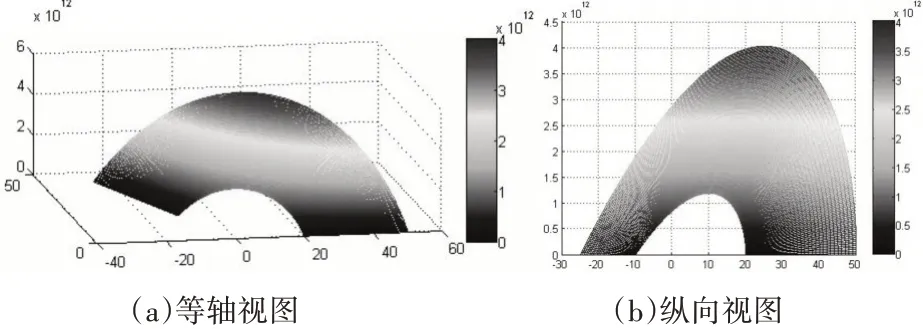
图8 当r=a自由，r=b自由时扇形环板挠度曲面

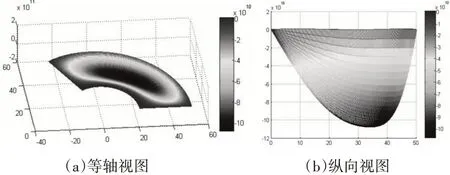
图9 当r=a固支，r=b固支时扇形环板挠度曲面

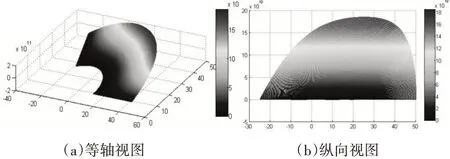
图10 当r=a固支，r=b自由时扇形环板挠度曲面

图11 当r=a自由，r=b固支时扇形环板挠度曲面

根据柱坐标系下扇形环板的挠曲微分平衡控制方程的通解表达式，利用“数值法”获得了该扇形环板在其它8 种边界条件下的挠曲形貌。当扇形板内外缘边界条件分别为，1）r=a简支，r=b固支；2）r=a 简支，r=b 自由；3）r=a 自由，r=b 简支；4）r=a 简支，r=b 简支；5）r=a 自由，r=b 自由；6）r=a 固支，r=b固支；7）r=a固支，r=b自由；8）r=a自由，r=b固支时，扇形环板挠度曲面图如图4～11。

4 结语

1）研究讨论了直角坐标系下矩形薄板在横向载荷、纵向载荷、横纵向载荷作用下板的小挠度挠曲微分平衡方程。

2）建立了基于柱坐标系下扇形环板的挠曲微分平衡控制方程，并解得该四阶微分方程的通解表达式如下:

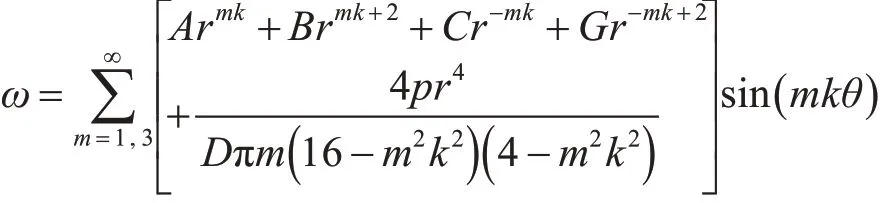
并利用“数值法”获得了该扇形环板在9 种边界条件下的挠曲形貌。