基于WTVS 模型的电力系统短期负荷预测∗

何华琴 何后裕

（国网泉州供电公司 泉州 362000）

1 引言

负荷预测一直是电力系统重要的研究课题，负荷预测的准确性直接影响发电计划的制定，对电力系统的运行与调度至关重要。短期负荷预测能够从几小时到几天的时间，根据历史负荷数据和实时负荷数据出发，计算出未来某特定时刻的电力负荷数值。影响负荷变化的因素有很多，如季节因素、经济因素和随机因素等。短期负荷预测中，天气因素和随机因素是最重要的影响因素。而季节和温度对负荷的影响最大，这是因为温度的变化直接导致加热和制冷设备的能耗变化。诸如大型体育赛事等随机因素会在特定的时间内改变电力需求消耗量，这将导致突然的负载变化。

在过去研究中，已经提出了许多负荷预测模型。这些模型可分为传统方法［1］和人工智能方法［2］，前者包括回归模型、时间序列模型等，后者提供了许多用于预测短期负荷的新工具，如神经网络［3～5］、模糊逻辑［6～7］、支持向量机［8］、专家系统［9］、混合方法［10～11］等。近年来，许多研究人员使用模糊时间序列模型来处理负荷预测问题［12～14］。文献［15］提出了一种用于短期负荷预测的时变滑动模糊时间序列模型（TVS），而TVS 模型仅使用历史数据来预测负荷变化。

本文考虑到季节、温度和随机因素的影响，提出了加权时变滑动模糊时间序列预测模型（WTVS）。将WTVS 模型分为三个部分，包括数据预处理、趋势训练和负荷预测。在数据预处理阶段，通过平滑历史数据来削弱随机因素的影响。在趋势训练和负荷预测阶段，将季节性因素和历史数据的权重引入TVS 模型。利用国网陕西省电力公司的负荷对WTVS 模型进行了测试。结果表明，与TVS模型相比，WTVS 模型在负荷预测精度方面实现了显著的改善。

2 时变模糊时间序列

定义在论域U={u1,u2,…,un}中的模糊集A可以表示为A=，其中 fA是模糊集 A的隶属函数，fA:U →[0,1]，fA(ui)表示ui对模糊集A 的隶属度，fA(ui)∊[0,1]且 i ∊[1,n]。

定义1:令Y(t)(t=…,0,1,2,…) 为论域且为R 的子集。假设 fi(t)(i=1,2,…)由Y(t)定义，F(t)是 fi(t)的集合，则F(t)被称为Y(t)上的模糊时间序列。

定义 2［16］:假设 F(t) 是一个模糊时间序列，F(t)=F(t-1)×R(t,t-1) ，其中 R(t,t-1) 是模糊关系，×是由F(t-1)引起的算子。当F(t)=F(t-1)×R(t,t-1)是F(t)的一阶模糊时间模型时，F(t)和F(t-1)之间的关系可以用F(t-1)→F(t)来表示。

定义3:设F(t)是一个模糊时间序列，对于任何t ，F(t-1)=F(t) 和 F(t) 只有有限元，因此 F(t)是时不变模糊时间序列；否则，它是一个时变模糊时间序列。

定义 4:如果 F(t) 是由 F(t-1),F(t-2),…,F(t-n) 构成，则用 F(t-1),F(t-2),…,F(t-n)→F(t)表示模糊关系，它是n 阶模糊时间序列模型。

定义 5［17］:假设 F(t) 是由 F(t-1),F(t-2),…,F(t-m)(m ＞0)构成且关系是时变的。 F(t)是一个时变模糊时间序列，其关系可以表示为F(t)=F(t-1)×Rw(t,t-1)，其中 w ＞1 是影响预测 F(t)的时间参数，则w 是时变模型的分析窗口。

3 WTVS模型

3.1 主要思路

本研究旨在利用自适应算法改进短期负荷预测，在加权历史数据的训练阶段自动调整分析窗口，并利用启发式规则在测试阶段进行负荷预测。WTVS 模型包括以下步骤:1）预处理历负荷史数据，2）定义和划分论域，3）定义模糊集和模糊化时间序列，4）建立模糊关系，5）预测和去模糊预测结果。这些步骤包括三个部分:预处理阶段、训练阶段和测试阶段。预处理阶段通过平滑历史数据来消除随机因素的影响，训练阶段用于数据学习。根据选定的分析窗口大小且在每轮中计算两个值，并将具有较高预测精度的值确定为预测值。在这个过程中，得到了分析窗口的序列。分析窗口的选择由自适应算法（算法1）确定。

测试阶段用于预测精度测试。根据测试阶段的选择的分析窗口大小，由算法3 计算每个测试数据的两个值。考虑到季节因素的影响，提出了一种启发式方法用于选择测试阶段的分析窗口大小，并根据训练阶段获得的分析窗口序列确定预测值。WTVS模型的结构如图1所示。

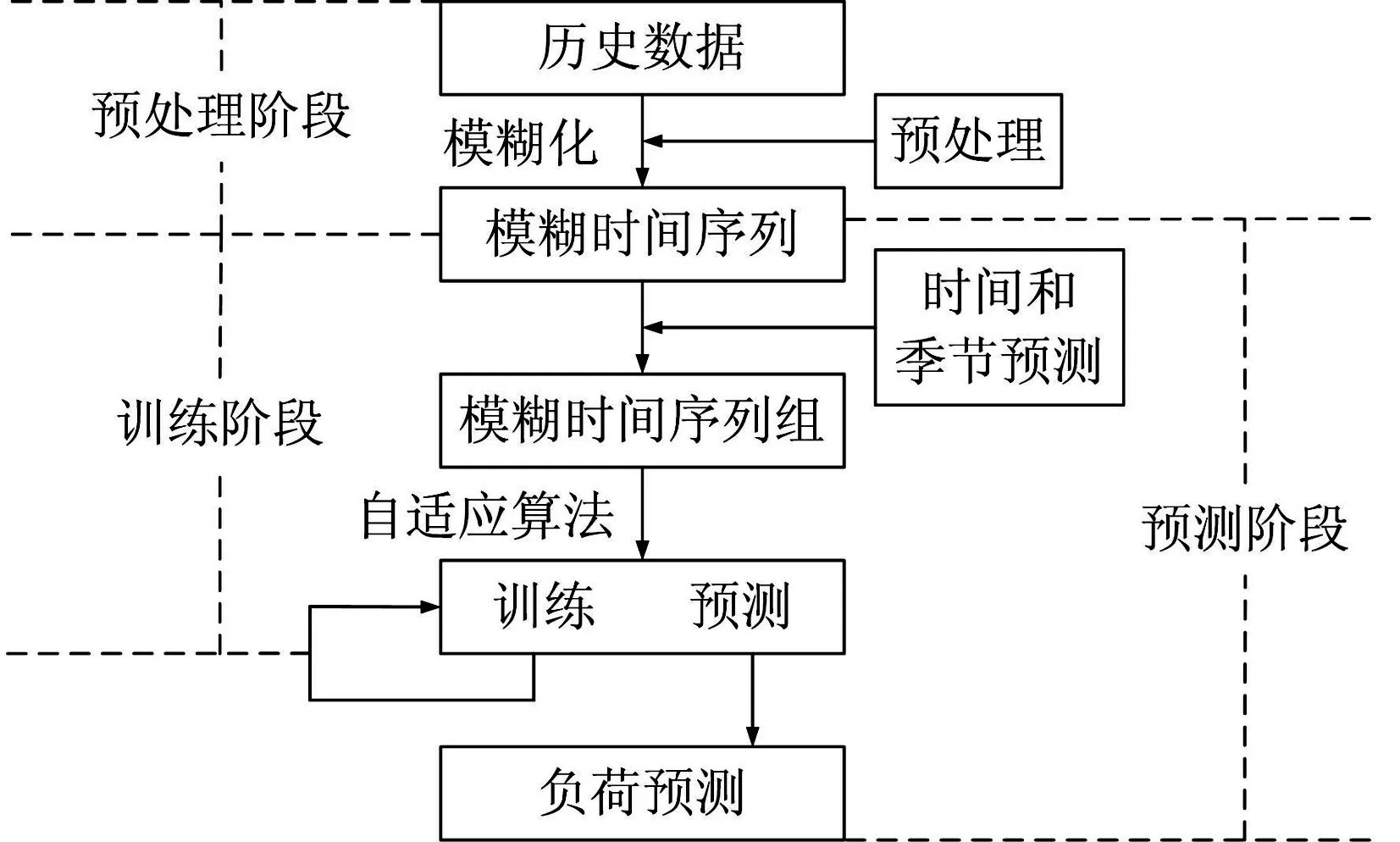
图1 WTVS模型

3.2 具体步骤

以下描述每个步骤的具体细节:

步骤1:预处理历史负荷数据。随机因素可能导致突然的负荷变化。当负荷的绝对差值高于阈值时，本文将通过下面的方法平滑这些突然的负荷变化。阈值α 定义为

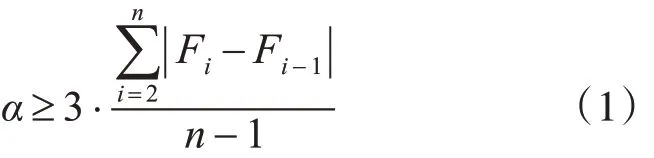
假设 |Fi-Fi-1|≥α ，则本文将用 Ft-1+α 代替Ft。

步骤2:对预处理的历史负荷数据进行模糊化。

1）定义论域U=[Lmin,Lmax]并将其分离成m 个区间 u1,u2,…,um，ui=[Lmin+(i-1)l,Lmin+il] ，其中l 是区间长度，ui的中点是mi。

2）定义模糊集Ai并对数据进行模糊化:

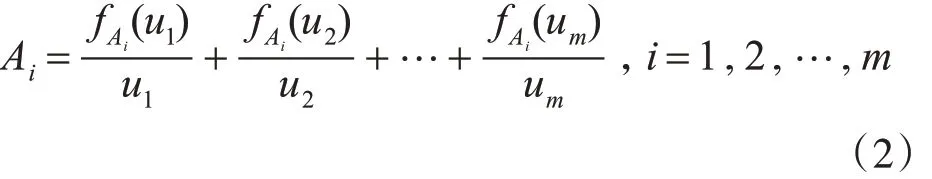
步骤3:建立时间t 和t+1 的模糊关系，并对模糊时间序列进行分组。

在训练阶段，模糊关系为Ai→Aj。在测试阶段，模糊关系为Ai→#。

一般来说，夏季和冬季的负荷趋势分别如表1和表2中所示。例如，在夏季可以得出结论:从1点到6 点，负荷呈下降趋势，而从7 点到12 点，负荷呈上升趋势。这些趋势可以用来修正预测阶段的预测。

表1 夏季负荷趋势

表2 冬季负荷趋势

步骤4:预测和去模糊化预测结果。

在训练阶段，每轮计算两个值，即CV1和CV2，将两个值与实际负荷值进行比较，并将较好的值作为预测负荷值。分析窗口由算法1 确定。通过算法2 进行CV1和CV2的计算。在测试阶段，每轮计算两个值，即CV3和CV4，预测负荷由算法3确定。

3.3 滑动分析窗口（算法1）

步骤1:i=1，Si=1，Si+1=2，其中 Si和 Si+1是初始窗口的大小并标记n=1；

步骤2:如果Si计算的预测精度高于Si+1，则将分析窗口向前滑动，分析窗口的大小加上1 并标记n=n+1。否则，幻灯片分析窗口向后滑动，分析窗口的大小减去1并标记n=n-1。

步骤3:重复步骤2直到训练数据结束。

3.4 训练阶段（算法2）

假设时间k 和k+1 的模糊关系是 Ai→Aj，分析窗口的大小是n。设M[Aj]为区间uj的中间值。

步骤1:令n=1，选择两个初始窗口的大小为S1=1和S2=1；

步骤2:若 n=1，则CV1=M[Aj]，若 n ≥2，则

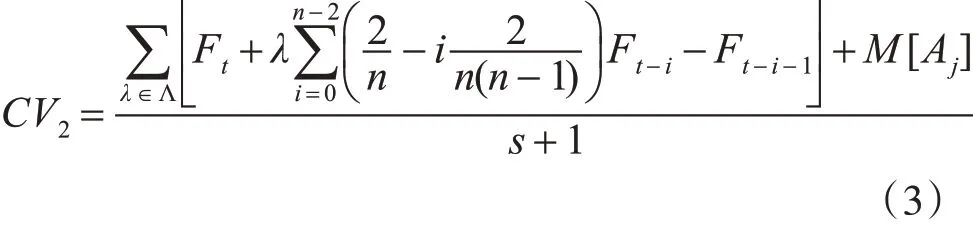
如果式（4）成立:

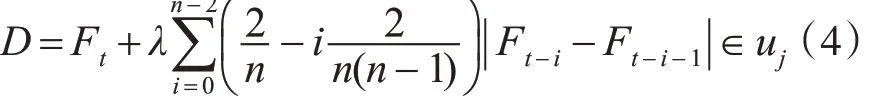
则 s=s+1时，λ ∊Λ 。否则，s=s 时，λ ∉Λ 。

步骤3:与实际负荷相比，如果CV2的训练精度高于CV1，则预测负荷Fp为CV2，否则，预测负荷 Fp为CV1；

步骤4:将分析窗口滑动到整个训练数据的末尾。

3.5 预测阶段（算法3）

假设时间k 和k+1 的模糊关系为 Ai→#，分析窗口的大小是n，M[Aj]是区间uj的中间值。

步骤1:令n=1，选择两个初始窗口的大小为S1=1和S2=1；

步骤2:若 n=1，则CV3=M[Aj]，若 n ≥2 ，则

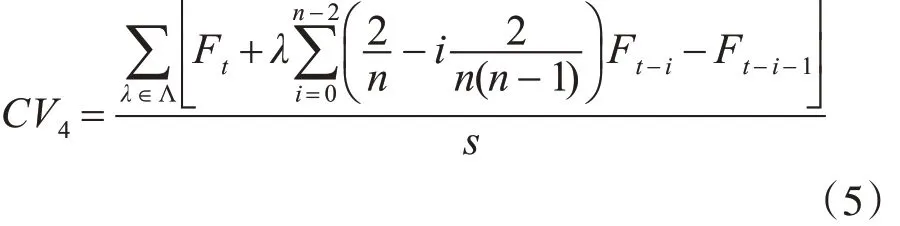
如果式（4）成立，则 s=s+1 时，λ ∊Λ 。否则，s=s 时，λ ∉ Λ ；

步骤3:考虑负载变化的趋势和训练阶段获得的标记n 的顺序，有以下启发式规则:

1）如果 nt＞nt-1，时间 t 的实际负荷大于时间t-1 的实际负荷，则时间t+1 的负荷呈上升的趋势。同时结合表1 和表2 的趋势，预测值为CV3和CV4中的最大值。

2）如果 nt＜nt-1，时间 t 的实际负荷小于时间t-1 的实际负荷，则时间t+1 的负荷呈下降的趋势。同时结合表1 和表2 的趋势，预测值为CV3和CV4中的最小值。

3）如果 nt=nt-1，预测值是 CV3和 CV4的算术平均值。

步骤4:将分析窗口滑动到整个训练数据的末尾。

4 实验分析

本文利用国网陕西省电力公司的负荷数据验证模型。通过比较所提出的WTVS 模型的预测负荷与TVS 模型的预测负荷，验证WTVS 模型的性能。考虑到时间和季节因素，本文选择每天的1 点到24 点的数据作为研究数据。数据分为两部分:训练数据（从1 点到20 点）和预测数据（从21 点到24 点）。表 3 通过预处理列出了 2018 年 5 月 23 日和2018年6月29日的负荷。

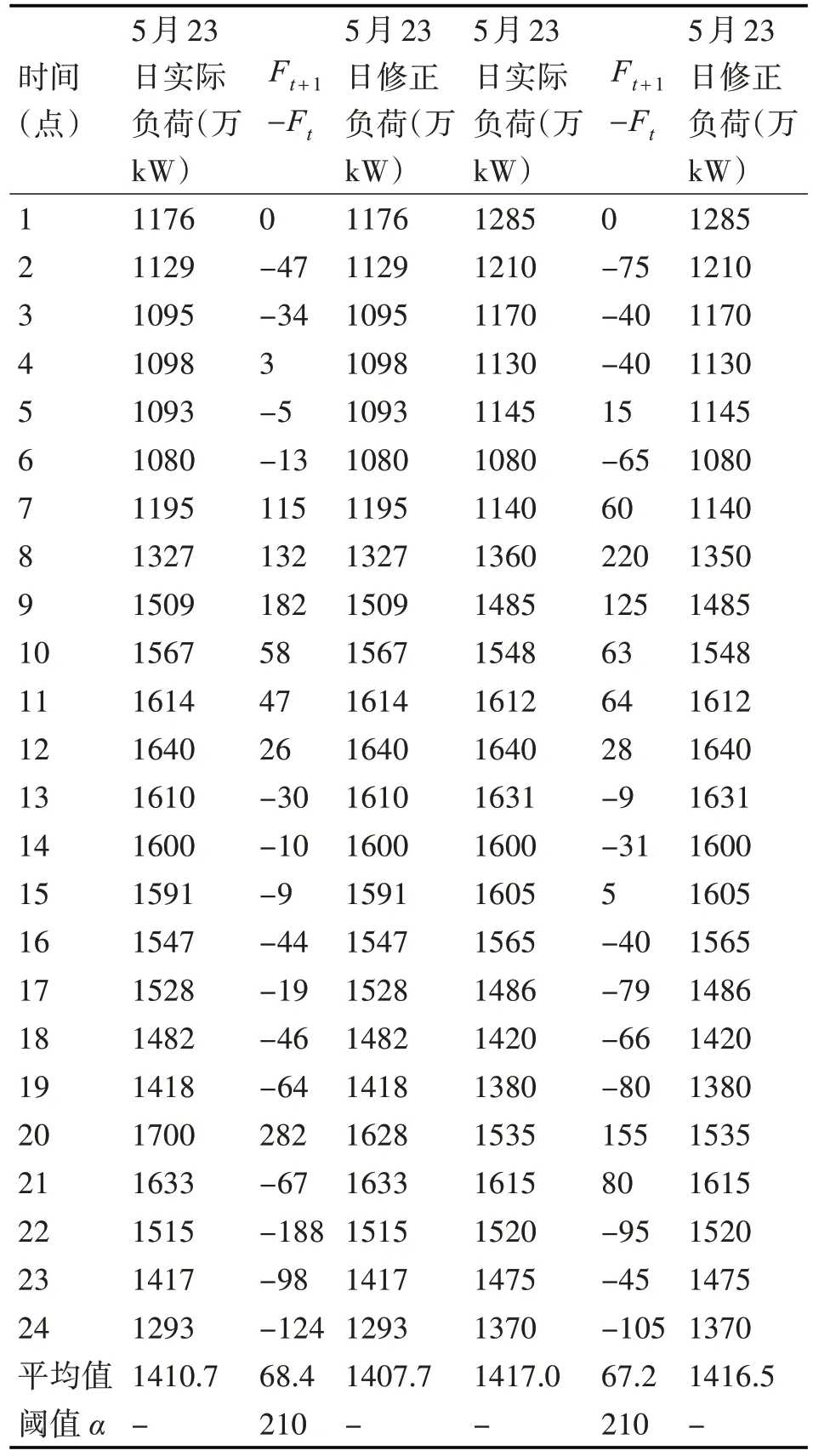
表3 负荷预测

为了比较预测精度，本文使用平均绝对百分误差（MAPE）作为预测精度的指标。MAPE定义为

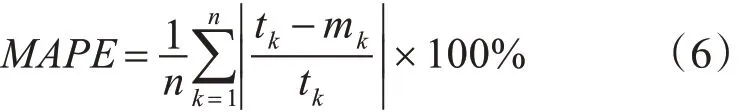
其中，tk和mk分别代表第k 个数据的实际值和预测值，n 代表数据的数量。表4 比较了具有相同间隔数的预测阶段中WTVS 模型和VTS 模型之间的预测数据（从21 点到24 点）结果。MAPE 结果表明WTVS模型优于TVS模型。

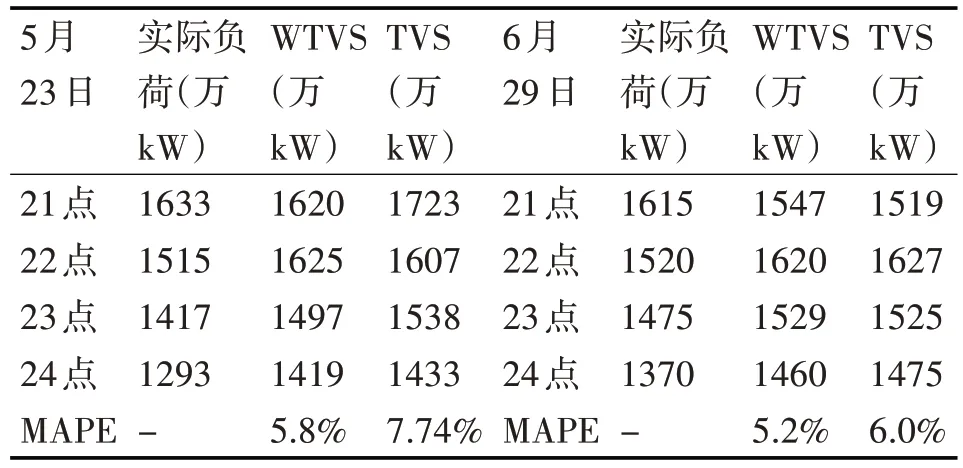
表4 预测阶段中WTVS模型和VTS模型比较

表5 给出了在不同间隔数下预测阶段的不同预测精度。结果表明，预测精度受区间长度的影响。

表5 在不同间隔数下预测阶段的比较

5 结语

本文提出了一种用于短期负荷预测的加权时变滑动模糊时间序列模型（WTVS），并利用国网陕西省电力公司的负荷数据验证了WTVS 的有效性。WTVS 模型在训练阶段生成的一些启发式知识用于计算预测值。实验结果表明，WTVS 模型比TVS 模型更为精确。并且WTVS 模型的优点如下:1）WTVS 模型中考虑了外部因素。在数据预处理阶段，通过平滑历史数据来削弱随机因素的影响。在趋势训练和负荷预测阶段，将季节因素引入TVS模型。2）WTVS 模型中考虑了加权历史数据，这对不断更新的历史负荷数据在计算中的表现更加提高了预测精度。