多步强化学习算法的收敛性分析∗

杨 瑞

（天津大学数学学院 天津 300072）

1 引言

强化学习（Reinforcement Learning）［1］是解决这样一个问题的机器学习分支:智能体（Agent）与环境交互，如何自动地学习到最佳策略以使自身获得最大回报（Rewards）。最近 AlphaGo［2］击败了人类顶尖围棋职业选手，其核心技术之一就是强化学习。强化学习在现代人工智能学中有着举足轻重的地位，有着广泛的应用前景［3～4］。

强化学习是一种不告诉Agent如何去正确地决策，而是让Agent自己去探索环境，在与环境交互的过程获得知识，不断优化策略。Agent 与环境交互的过程如下:

1）Agent感知当前环境状态s；

2）针对当前环境状态s，Agent根据当前行为策

马尔科夫决策过程（MDPs）是强化学习的基本框架［5］，可以由四元组＜ S ，A ，P，R＞来表达。 S 是系统的有限状态集，A 是Agent 的有限动作空间，动作用来控制系统的状态转移，:S×A×S'→[0,1]为Agent执行动作a 之后，系统由状态s转向s'的概率。:S'×A×S'→1R 表示当 Agent 执行动作a，系统由状态s 转到状态 s'后，系统反馈给略选择一个动作a；

3）当Agent选择a，环境由状态s 转移到当前状态 s'，并给出奖赏值（Rewards）R；

4）环境把R反馈给Agent。

如此循环此过程，直至终止状态，在这个过程中，并没有告诉Agent 如何采取动作，而是Agent 根据环境的反馈自己发现的。

1.1 马尔科夫决策过程（MDPs）

Agent的rewards。

策略（policy）定义了Agent 在给定状态下的行为方式，策略决定了 Agent 的动作。 π:S×A →[0,1]，π（s,a）表示在状态s 下，执行动作 a 的概率。

在MDP 中，还定义了两种值函数（Value Function）:状态值函数Vπ(s)（State Value Function）和状态-动作值函数 Qπ(s,a)（State-act Value Function）。

Vπ(s)表示 Agent 从状态 s 开始，根据策略 π 所获得的期望总回报（Rewards）:

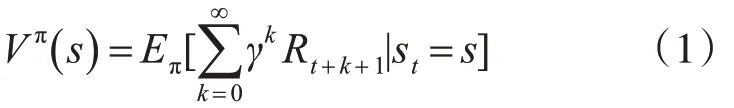
类似地:

值函数的确定了从一个状态出发，按照π 所能获得的期望总回报。

1.2 Bellman 方程

由于MDP 中，状态转移满足Markov 性，1957年，Bellman证明了他的著名方程［6］:

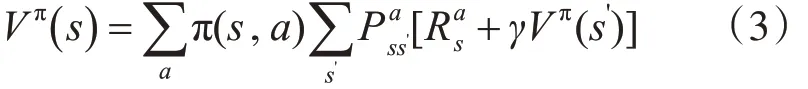
类似地:

由此可知:系统的状态转移矩阵和回报均已知，则易求出Vπ(s)和 Qπ( )s,a强化学习的目标是导出最优策略π*:

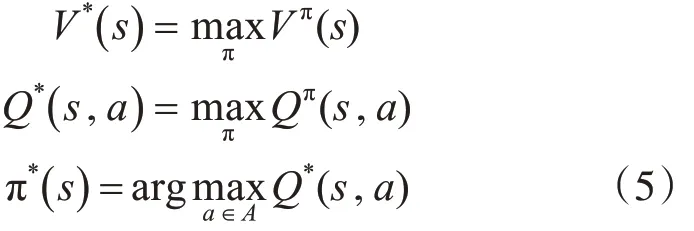
1.3 模型未知的强化学习

MDPs 为强化学习提供了统一的框架，但实际问题中有如下几个问题:

1）“维数灾难”:状态空间超级巨大，要学习的参数随着状态空间的维数指数级爆炸。

2）收敛速度慢:很多强化学习算法的收敛性分析都要依赖“任意状态都要被无数次访问到”这样的前提条件。

3）很多实际问题，我们是无法获得系统的状态转移概率和回报函数的，对这种情况建立模型的算法称为模型未知的强化学习算法。

最近，有研究人员提出 Q(σ) 算法来估计Qπ(s,a)，并且原文作者通过实验发现收敛效果很好。本文将对Q(σ)的收敛性给予一个证明。

2 时间差分学习算法框架

时间差分算法（Temporal Difference）是强化学习最核心的一类算法，这项工作首次是在Suton 1988［7］年提出的。这类算法不需要知道系统的状态转移矩阵，能够直接学习。假设Agent 在与环境交互中产生的一个轨道为

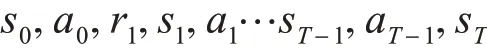
其中sT是终止状态。

2.1 Sarsa算法

Sarsa［8］算法是根据上述轨迹来迭代 Bellman 方法的解，其名称是由Agent学习的数据结构而来的，数据是由一个(st,at)转移到下一个(st+1,at+1)的五元组(st,at,rt+1,st+1,at+1)

Sarsa估值计算公式为

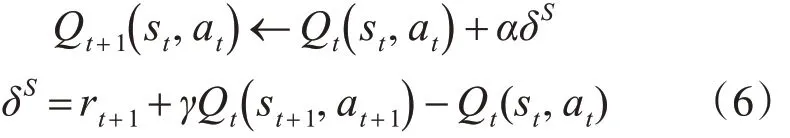
α 为学习率，δ 称为Sarsa算法的时间差分。

2.2 Expected Sarsa算法

Expected Sarsa［9］:

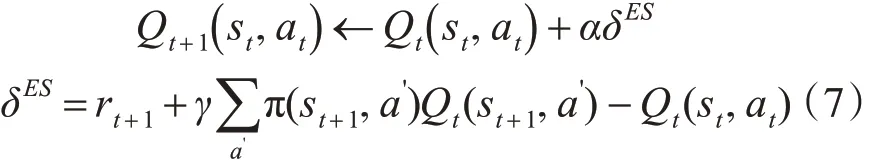
由Sarsa 和Expected Sarsa 的迭代形式可知，Sarsa 是一个全采样的算法，即在t 时刻，只用rt+1+γQt(st+1,at+1) 来作为目标（target）进行估值。而Expected sarsa 是采用下一状态st+1的Q 值的期望 :来估值。根据Bellman 等式（4），从直觉上讲，Expected Sarsa 的估值要稳定一些［10］。首次证明了 Expected Sarsa 和Sarsa 有相同的 bias，但是 Expected Sarsa 的方差更小一些。

2.3 Q(σ) 算法

Q(σ)［11］算法的设计思想是:引入了参数 σ ，σ是采样的程度，如果σ=0，表示no-sampling，σ=1表示full-sampling。

单步Q(σ)算法的迭代形式:

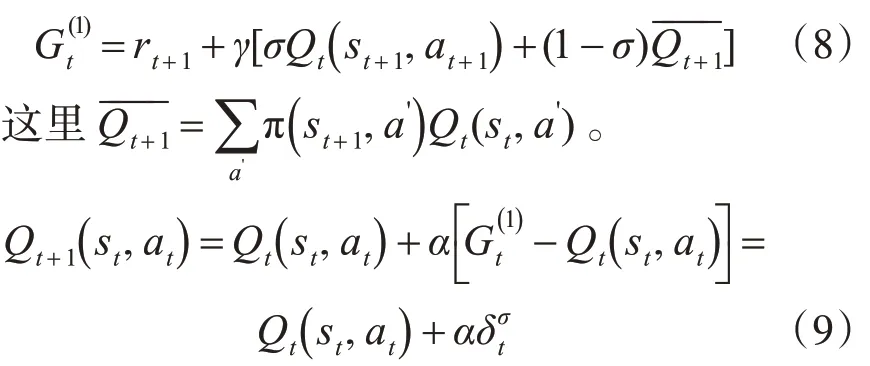
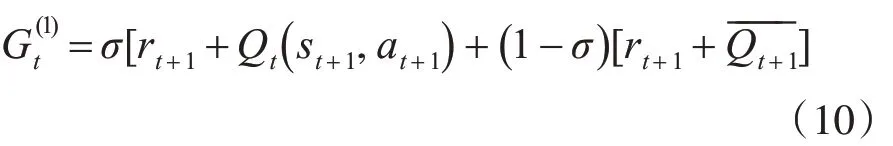
2.4 多步时间差分算法

Sarsa，Expected Sarsa，Q(σ)［12～14］均可以推广至多步的情况。

2.4.1 多步Sarsa

多步Sarsa值函数的估计公式:

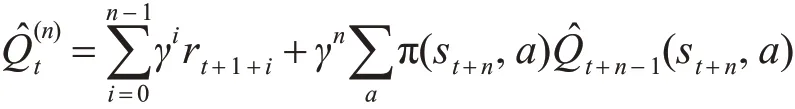
多步Sarsa值函数的更新公式:

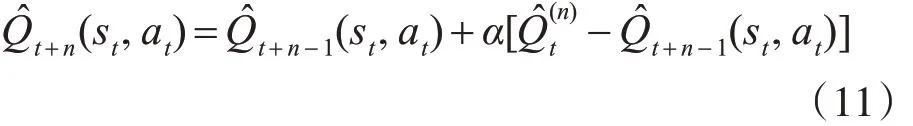
2.4.2 多步Expected Sarsa 算法，也称多步Tree Backup算法

多步Expected Sarsa也是类似的，但有一些差别。

多步 Expected Sarsa［11］值函数的估计公式:

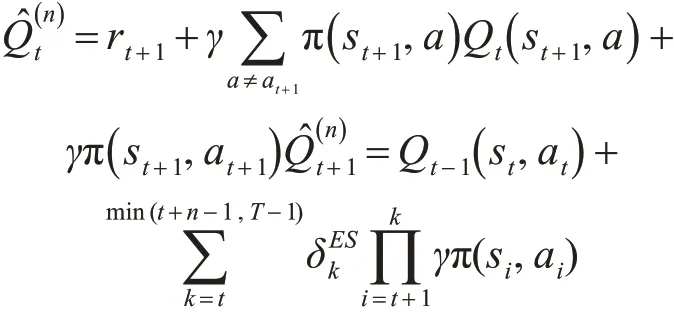
多步Expected Sarsa值函数的更新公式:

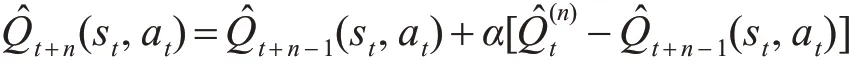
2.4.3 多步 Q(σ)

多步Q(σ)值函数的估计公式:

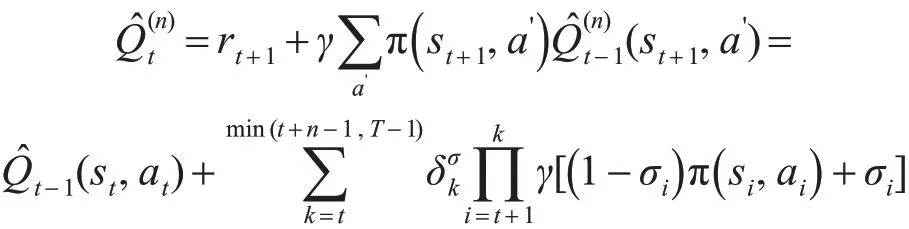
多步Q(σ)值函数的更新公式:

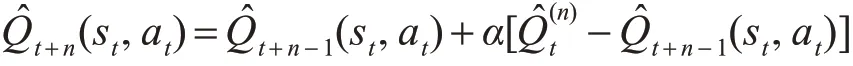
3 Q(σ)算法的收敛性分析

引理 1［15～16］:假设一个随机过程 (ζt,Δt,Ft) ，ζt,Δt,Ft:X → R 满足方程:

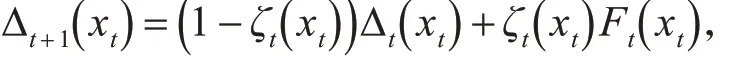
这里 xtϵX,t=0,1,2,… 假设 Pt是 σ -fields 的递增序列，ζ0，Δ0是 P0-measurable，ζt，Δt以及Ft-1是 Pt-measurable，t ≥1。假定以下条件成立:

1）X是有限集；

2）ζt( xt)∊[0 ,1],∑tζt( xt)=∞,∑t(ζt( xt))2＜ ∞

w.p.1且∀x ≠ xt:ζt( x )=0；

3）∥E{Ft|Pt} ∥≤ κ ∥ Δt∥ +ct，κ ∊[ 0,1),ct依概率收敛于0；

4）Var{Ft( xt)|Pt} ≤K(1 +κ ∥ Δt∥ )2,K 是常数。

其中∥⋅∥表示最大模；则Δt依概率收敛到0。

定理1:在MDP 框架下，对于任意的初始化Q( s,a), ∀ γ ∊ ( 0,1) 。

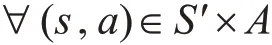
Q的更新按以下方式:

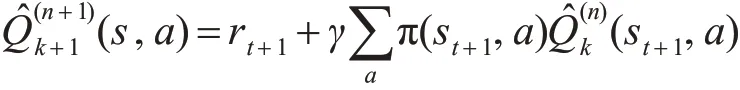
令 Δn=-Qπ(s,a) ，则 有 ||Δn+1||≤γ||Δn||，Δn按最大值范数是压缩序列，即 Δn依概率收敛于0。

证明:由数学归纳法证明之。

For n=1:

假设对n也成立:

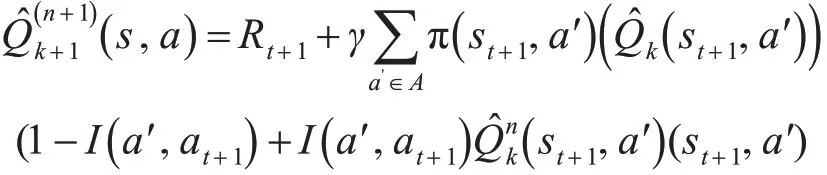
这里I( )aʹ,at+1是一个指示函数:

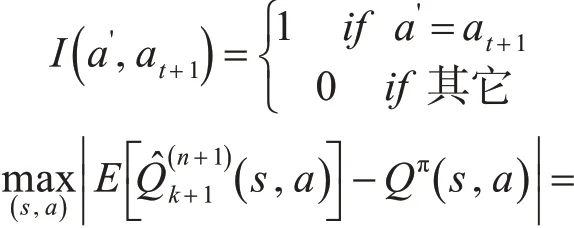
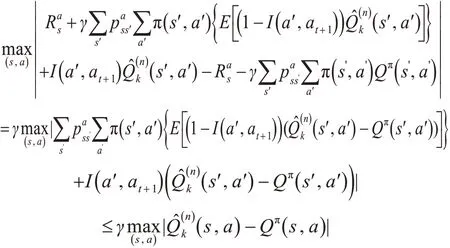
定理2:在MDP 框架下，对于任意的初始Q( s,a),∀ γ ∊( 0,1) 。

事实上，如果定理1中的 π(st+1,aʹ)满足:

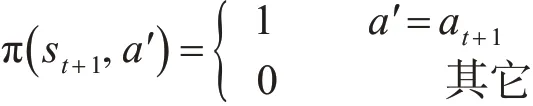
则这就是式（11）所表示的算法，也即是定理1中算法的特殊情况，由定理1 的收敛性可以得到该算法也是收敛的。

定理3:如果Q(σ)算法满足条件:

1）状态空间是有限集；

则Q(σ) 迭代产生的Qt(s,a) 依概率收敛于Qπ(s,a)。

定理3的证明:

Q(σ)是定理1 和定理2 所述算法的凸组合，易知 Q(σ) 迭代产生的 Qt(s,a) 依概率收敛于Qπ(s,a)。

4 结语

本文以时间差分学习算法为主线，系统简要地介绍了强化学习中的几个重要估值算法，并对最近提出的一个新的时间差分学习算法Q(σ)算法作了理论分析，同时给出了Q(σ)算法的收敛性证明，这在强化学习理论研究中具有重要意义。