基于方差模型的体育赛程主客场安排对赛事的影响分析∗

刘引涛 刘 楠

（陕西工业职业技术学院 咸阳 712000）

1 引言

体育赛程中不同球队在规定天数内进行比赛，除了受天气、场地、身体因素［1～3］等原因影响外，在不同球队根据赛程安排抽签比赛过程中，也会面临每一个球队随机面临与其他球队的随机参赛情况［4～5］，这些都会对比赛结果产生各种影响，通过数学建模的手段对体育赛事进行理性和量化的分析［6～8］，是评价与优化赛事安排与管理［9］、预测赛事结果［10］、提高赛事公平公正性［11～12］的重要手段之一。通过对国际赛程安排中分区和排名等数据的分析，综合考虑分析赛程安排中主客场对某一支球队的利弊，将赛程的数据转化成适合数据处理的数字格式，建立基于方差的数据模型，分析出评价赛程利弊的数量指标。

2 问题分析

首先分析要考虑影响赛程安排公平性的因素:球队在比赛过程中队员应保证有足够的休息时间；同时，球队之间有主客场的分布，对于比赛时主客场气氛和环境因素会影响主队与客队的发挥，而主客场的数量值对每个队都是相等的，因此考虑主客场排布规律对球队发挥的影响（如主场到客场，主场到主场，客场到主场，客场到客场的影响规律）从而确定分析问题的因素。分析主客场影响，考虑主客场变化过程中对队员适应程度及疲劳程度的影响，给予主客场变化影响系数，建立主客场平均值与相对差分析的方法［13～14］，给出评价标准。

3 模型假设

安排赛程时不考虑球队的强弱；球队打客场时行程远近对球队水平的发挥无影响；不考虑天气、裁判、伤停对球队的影响。

4 模型建立

分析主客场因素对球队水平发挥的影响主要体现在主客场变化过程中对队员适应程度及疲劳程度的影响，建立如下模型:

用aki表示第k 个球队第i 次参赛时的主客场情况。

aki为0 表示第k 个球队第i 次参赛分布为客场；

aki为1 时表示第k 个球队第i 次参赛分布主场，即

引入向量(aki,aki+1)来表示相邻两场比赛所处的主客场情况，当相邻的两场比赛都为主场时则不会对参赛队造成影响，对于它的实力的发挥的影响系数我们可以用1 表示。当前一场为客场后一场为主场的时候，在这个过程中对于参赛队而言将会是一个由消极环境向积极环境转变的过程，对于参赛队员而言应会有较好的发挥，但相对于前面介绍的情况系数则会相对低些，根据实际情况将其实力发挥的影响系数系数表示为0.9。当前一场为主场而后一场为客场的时候，对于参赛队而言将会是从有利环境向不利环境转变，这样会对参赛队而言其发挥的将会不太理想，则相对于前面介绍的情况系数则会相对低些，根据实际情况将其实力发挥的影响系数表示为0.8。当前一场为客场而后一场同样也为可长的时候，对于参赛队将会是从消极环境向消极环境的转变的过程，对于参赛队而言其水平发挥将会达到一个不理想，则相对于前面介绍的情况系数则会向南队会低些，根据实际情况将其实力发挥的影响系数表示为0.7。

对于一参赛对而言相邻两场比赛的主客场之间的排布对比赛的胜负的影响系数Mi的具体排列如下所示:

当 (aki,aki+1)=（1，1）时，用M1表示主场——主场且 M1＝1；

当 (aki,aki+1)=（0，1）时，用 M3表示客场——主场且M3=0.9；

当 (aki,aki+1)=（1，0）时，用M2表示主场——客场且M2=0.8；

当 (aki,aki+1)=（0，0）时，用M4表示客场——客场且M4=0.7。

从主客场的优势可以得到:M1＞ M2＞ M3＞ M4。

在考虑主客场安排对参赛队得利弊得时候，使用C 语言［15］程序模拟出主客场排布的4 种不同的情况下的实际排列数量，既统计主客场转变数（主程序见附录部分）。

J表示在整个比赛过程中主场——主场出现的次数；

N 表示在整个比赛过程中客场——主场出现的次数；

K 表示在整个比赛过程中主场——客场出现的次数；

M 表示在整个比赛过程中客场——客场出现的次数。

#include＜stdio.h＞

#define p 83

void main（）

｛ int N=0，M=0，K=0，J=0，i；

int a［p］；

printf（“请输入需要进行处理的组的相关主客数 ”）；

for（i=0；i＜p；i++）

scanf（“%d”，﹠a［i］）；

for（i=0；i＜p；i++）

｛

if（a［i］==0﹠﹠a［i+1］==1）

N++；

if（a［i］==0﹠﹠a［i+1］==0）

M++；

if（a［i］==1﹠﹠a［i+1］==0）

K++；

if（a［i］==1﹠﹠a［i+1］==1）

J++；

｝

printf（“第i场为客场，第i+1场为主场的组数为 ”）；

printf（“N=%d”，N）；

printf（“第i场为客场，第i+1场为客场的组数为 ”）；

printf（“M=%d”，M）；

printf（“第i场为主场，第i+1场为客场的组数为 ”）；

printf（“K=%d”，K）；

printf（“第i场为主场，第i+1场为主场的组数为 ”）；

printf（“J=%d”，J）；

｝

可以列出对于第k个参赛队的利弊程度Sk:

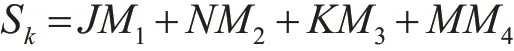
则可以求出总体主客场安排的影响平均值Sˉ:

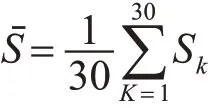
对此可以求出每个参赛队的Sk值相对于30个参赛队总体的值Sˉ的离散程度DKS，也就是用其DKS的大小建立方差模型，来作为衡量赛程的主客场安排对于一个队的利弊标准:

也就是说对于两参赛队而言其DKS值越大，赛程的主客场安排越利于这只参赛队。

5 结语

该方差模型的设计，能够说明每个参赛对的相对参赛总队来说，其离散程度值越大，赛程的主客场安排越有利于该队的比赛，用数据作为评价标准，能够反映整个赛程对于某一参赛球队安排的利弊，该模型及算法明确，简单易行，通过层层深入的方式来筛选处所需要的数据，可以作为体育赛程安排分析和评价的参考。