基于灰色理论的ofo 需求量短时预测∗
赵广元 尚秋燕
(西安邮电大学自动化学院 西安 710121)
1 引言
共享单车(ofo)作为2016年城市出现的一种新型共享经济产物,有效地解决了“最后一公里”的难题,它的一大特色就是寻找、使用、停放实现了随用随取、随停随放,真正体现了自行车的便利性,满足了大众群众的出行需求。同时,数量日益庞大的共享单车也因为乱停乱放、挤占公共空间等问题给城市管理带来了新的挑战[1~2]。在不改变既有的城市规划格局条件下,对ofo需求量的科学有效预测,对相应指标体系的制定(如规范ofo车辆投放秩序)起着越来越重要的作用。
短时预测方法经过几十年的研究已超过200种,基本可分为基于线性系统理论、基于非线性系统理论、基于知识发现模型、基于动态交通分配模型和基于交通仿真模型等[3]。常用的预测方法有时间序列模型,卡尔曼滤波模型,非参数回归法,人工神经网络,支持向量机,灰色模型。时间序列模型建模简单,在数据充足及交通量周期性平稳变化的情况下,预测精度较高,但在数据有缺失、路段交通量受随机因素干扰大、不确定性强时,预测误差较大[4~5];卡尔曼滤波理论以线性理论为基础,因此对非线性、不确定性大的短时交通流,其预测误差较大[6];近邻非参数回归法误差小,预测精度高,其缺点是要求历史数据足够丰富,寻找“近邻”的工作量较大[7];神经网络学习模式需要大量原始数据训练,数据不足或数据有噪声都将导致预测结果偏差较大对交通信息的实时采集要求较高[8]。大部分模型普遍存在着“长周期、大区域、低信度”的缺陷,它需要大量的历史数据,灰色系统理论主要研究“小样本、贫信息”的不确定系统,在预测中得到了广泛的应用[9]。
灰色GM(1,1)模型利用累加生成后的新数据建模,其作用是弱化原始数据的随机性,容易找出数据变换规律,更加容易逼近非线性函数,它适应于变化趋势较明显的时间序列,却对随机波动大的时间序列则无能为力,而灰色马尔可夫预测模型先采用GM(1,1)模型拟合交通系统的发展变化趋势,再对随机波动大的残差序列进行马尔可夫预测,克服了灰色理论的不足[10~11]。本文则采用一种灰色马尔科夫组合模型,对ofo车流量进行短时预测,该预测只考虑基于道路某一断面的单点交通流量数据。仿真结果表明,该模型取得比较好的预测结果。
2 灰色理论
灰色理论由邓聚龙教授于20 世纪80 年代提出,它通过研究少量确切信息的数据样本,挖掘出未知的有用的信息,以正确认知系统的特性,并以此进行科学预测[12]。作为灰色理论内容之一的灰色模型(Grey Model),它通过对原始数据进行生成处理,来发现和掌握系统发展变动的规律,通过建立相应的微分方程模型,进而对系统的未来状态做出科学的定量预测[13-16]。
灰色模型GM(1,1)由单变量一阶微分方程构成,用于对系统主要因素进行拟合并预测,其主要的步骤为:对原始数据序列x(0)(t),计算一次累加,生成一个新的序列x(1)(t),将新序列x(1)(t)的变化趋势用常微分方程+dx(1)(t)=u 近似描述,之后用离散化和最小二乘法分别求出参数a 和u,获得灰色预测模型为
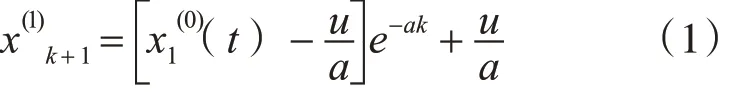
再做累减还原,获得预测数值:

3 马尔科夫预测
马尔科夫理论指出:“系统达到每一状态的概率仅与近期状态有关,在一定时期后,马尔科夫过程逐渐趋于稳定状态而与原始条件无关”的这一特性称为“无后效性”[17]。马尔科夫预测方法的特点是:不需要大量的统计资料,只需有限的近期资料即可实现定量预测,而且马尔科夫预测方法适用于短期预测的基础上,只要状态转移矩阵滚动次数足够多,同时也适用于长期预测[18]。许多事件发展过程的状态转移具有无后效,对于这样一些事件则可以利用马尔科夫预测。
3.1 状态转移概率
状态转移是指客观事物由一种状态到另一种状态的变化。由于状态转移是随机的,因此必须用概率来描述状态转移可能性的大小,将这种转移的可能性用概率描述,就是状态转移概率。对于由状态Ei 转移到状态Ej 的概率,称它为从i 到 j 的转移概率。公式表达如下:

3.2 状态转移概率矩阵
假定某一个事件的发展过程有n 个可能的状态,即 E1,E2,E3,…,En。记 Pij 为状态 Ej 的状态转移概率矩阵,则矩阵为

3.3 终极状态预测
在马尔可夫链中,己知系统的初始状态和状态转移概率矩阵,就可推断出系统在任意时刻可能所处的状态。以k 为时刻,πj(k)为状态概率(即事件在初始时刻k=0 状态己知的情况下,经过k 次状态转移以后,在第k 个时刻处于状态Ei 的概率),可以构造如下公式:

若记行向量 π(k)=[π1(k),π2(k),…,πn(k)],则由式(5)可以得到计算状态概率的递推公式:

利用式(6)可以计算π(0)在经过k 次转移后,在k 个时刻处于各种可能状态的概率,即π(k) ,π(k)则为该事件在k 个时刻的状态概率预测。经过无穷次状态转移后所得到的状态概率,则称为终极状态概率。记终极状态概率向量为π=[π1,π2,…,πn],按照极限定义可知:
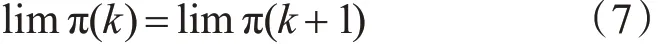

4 灰色马尔科夫模型建立
应用灰色一马尔可夫链方法进行预测的基本思路是:对采集到的交通流数据序列x(0)(t)先建立灰色GM(l,1)模型,求出其预测曲线Y(k),再以平滑的预测曲线Y(k)为基准,划分若干动态的状态区间,根据落入各状态区间的点,计算出马尔可夫转移概率矩阵预测未来状态,从而得出预测值区间,取区间中点,最终得到精度较高的预测值[19]。即灰色马尔科夫模型的建模思路如图1所示。
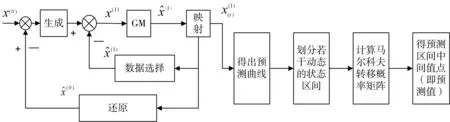
图1 灰色马尔科夫系统建模思路
其模型具体建模过程如下[20]:
设原始序列为x(0)=(,,…,)。
1)一次累加生成序列x(1)=(,,…,),其中:

2)确定矩阵B和Yn
设 z(1)是 x(1)的紧邻均值生成序列,紧邻均值生成序列 z(1)=(,…,) ,其 中=0.5(+),k=2,3,…,n。

3)用最小二乘法估算一阶线性微分方程的参数 aˆ,uˆ。
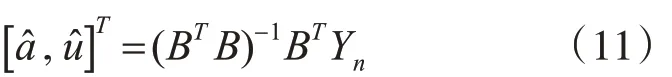
4)白化输出
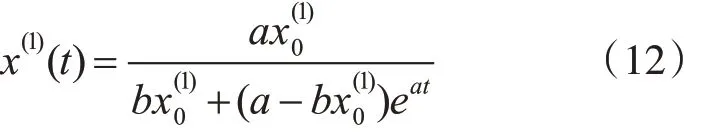
5)累减还原式

5 车流量预测模型实例分析
实验所用的验证环境是Windows10 系统下的Matlab2010a。以小寨十字路口路段2017 年9 月1日~9 月8 日共享单车(ofo)需求量的数据实测数据作为数据样本,其一周内的ofo出行需求变化如表1所示。
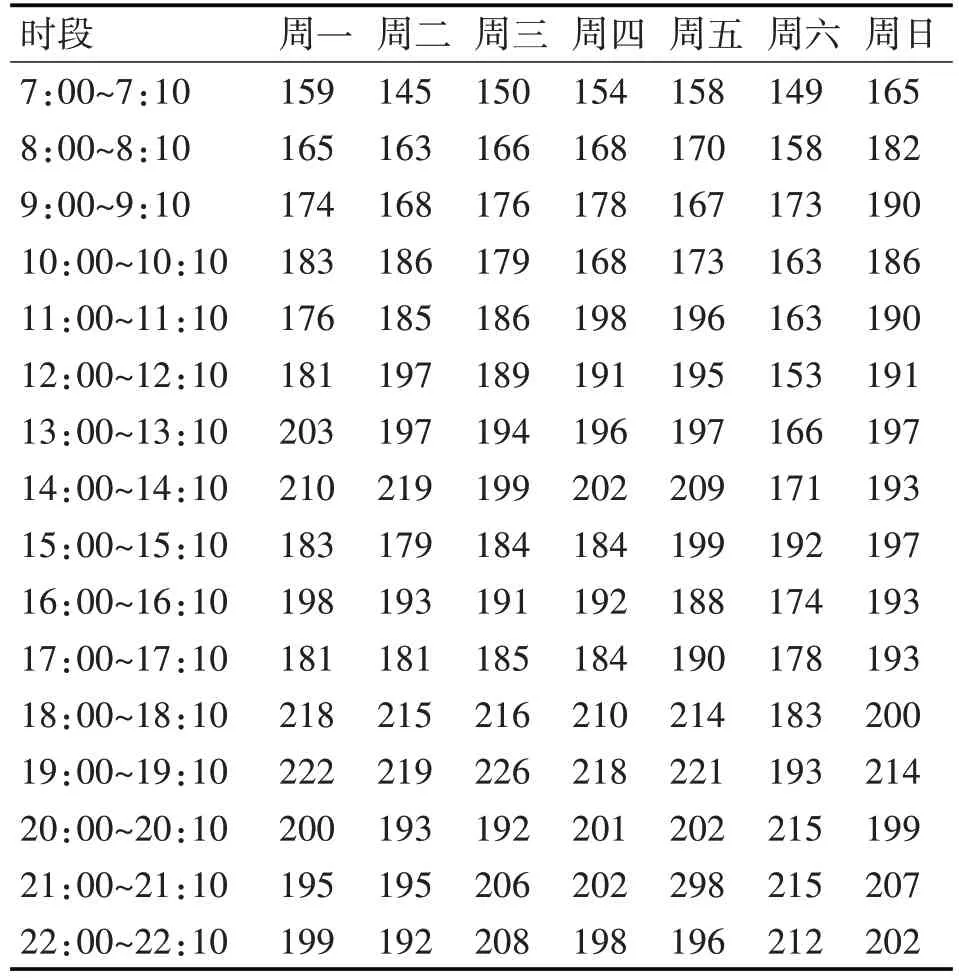
表1 白天ofo需求量统计表(单位:辆)
观测数据表1,以周六数据为例进行灰色马尔科夫模型的预测。将GM(1,l)模型方法和马尔科夫链优化的GM(1,1)模型所得发展系数和灰作用量分别代入式(13)中,运用Matlab R2010a 软件编写代码来实现2 种预测模型对数据的拟合及预测下一时间段ofo需求量,程序结果显示如表2。

表2 模型对比
为了更直观地进行比较,将上面的预测结果和实测值采用Matlab7.0 绘图工具绘于同一张图中,如图2所示。
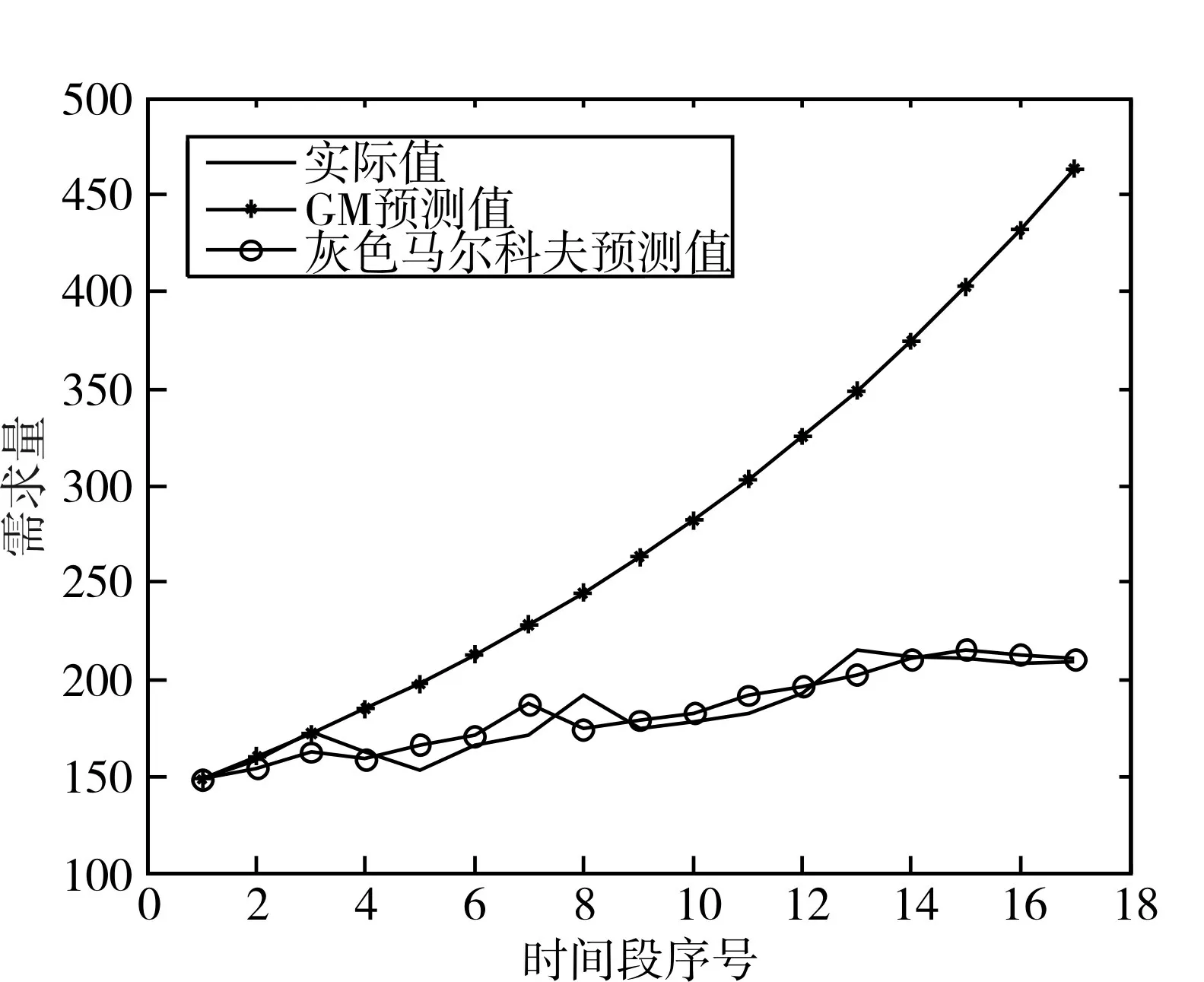
图2 ofo需求量实际值及2种预测值
参照灰色预测模型的精度检验等级表(表3)可知:灰色马尔科夫模型的平均相对误差均小于0.05,预测精度为二级(良),即模型精度为二级,可见模型精度较高。GM(1,1)模型适用于具有较强指数规律的序列,只能描述单调的变化过程,而马尔科夫模型则适用于非常单调的摆动发展序列或具有饱和状态的S 形序列。而本文所建立的灰色马尔科夫组合预测模型在一定预测时段内具有良好的预测精度和实用性,即该模型的预测性能更优、更实用。故该模型应用合理,比较适合用于某一时段内ofo需求量的短时预测。

表3 灰色模型精度检验等级
6 结语
针对交通系统这种复杂系统,相比于传统的灰色模型来说,本文采用的灰色马尔科夫组合预测模型能够达到在短时间内完成实时预测的要求,预测精度也令人满意,在一定程度上弥补了GM(1,l)的缺陷,当车流量的变化较大时,采用本方法可较好地改善十字路口的交通状况。通过理论研究和仿真实验可知,该灰色马尔科夫模型预测车流量结果符合要求,其预测有效,可用于需求量波动或饱和阶段的预测。

