一种新的小波阈值去噪算法在工程中的应用∗

李名莉 焦欣欣

（河南工业职业技术学院机电自动化学院 南阳 473000）

1 引言

在工程实际应用中，一些大型机械设备由于重复性工作致使故障频繁，一旦出现故障，会对企业造成极大的损失，须及时对故障诊断进行维修。现阶段常用的方法是对设备运行时采集到的振动信号分析处理，但工矿现场环境复杂，检测到的信号中都会夹杂着一些随机、高频的噪声信号，使信号的非平稳特性增加，对故障诊断结果产生影响，由此，在故障诊断之前需去除信号中的噪声信号。用传统傅里叶分析方法对信号处理会使故障信号淹没在振动信号中不易察觉，去噪效果不明显。而小波分析的正交分解和多分辨率分析处理信号的效果与实际信号很逼近，可以很好地解决暂态信号和非平稳信号，这是小波变换被用作分离噪声的原因所在［1～6］。

2 小波去噪算法

小波去噪算法主要分为三类:基于小波系数区域相关性的去噪方法、小波模极大值去噪方法和小波阈值去噪方法［7～9］。在三类算法中，前两类算法过程繁琐，计算任务大，使用较少。相比，小波阈值去噪算法过程简单，计算量小，容易掌握，该算法侧重于在对信号尺度分解后可在任意层次选择阈值，有效抑制噪声干扰［10～13］。

小波阈值去噪算法的关键点是对分解之后的信号分量作阈值的选取和阈值的量化，关联着信号的精度和连续性，设置一个合适的阈值可较大程度地提高去噪质量，提升信号诊断的精确度［14～15］。阈值过大，信号的细节分量就有可能过滤掉，过于平滑。阈值过小，致使信号中有大量噪声滞留，滤波效果不好。基于对阈值的处理，阈值去噪算法分为硬阈值处理和软阈值处理［1～4］。

3 小波去噪算法的改进

假设 f(k)是研究用的振动信号，混入噪声之后变为s(k)，建立一个噪声模型，表示如下:

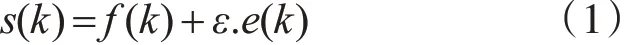
其中k=0,1,…n-1，e(k) 为高斯白噪声信号，ε为噪声强度。 f(k)表现为相对平稳或低频率信号，掺杂噪声后通常表现为非平稳的高频率信号。

对s(k)信号去噪，其实就是抑制e(k)信号恢复f(k)信号。要把 f(k)信号直接提取出来，对s(k)作离散小波变换，可得:

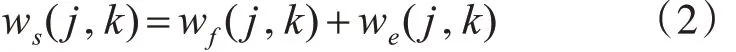
其中 j=0,1,2…J,k=0,1,2…N,J 为分解层数，N 为信号长度。假设 wj,k，μj,k，vj,k在第 j 层上的小波系数分别是ws(j,k)、wf(j,k)和we(j,k)，要想得到去除噪声后的真实信号 f(k) ，需要对f(k)的小波系数 μj,k作准确估值［8～12］。

去噪的主要思路是:选取一个阈值λ 与wj,k的大小比较，当 wj,k＜λ 时，wj,k≈vj,k，在这种情况下wj,k值与噪声是有关系的，可忽略不计；反之，则可说明wj,k值与原始的振动信号有关，可看作wj,k≈μj,k。

1）软阈值函数

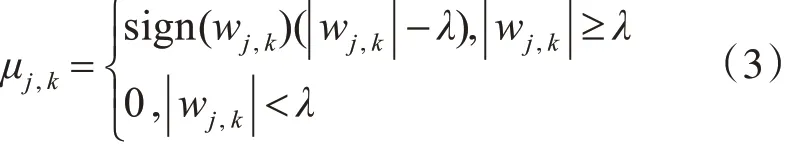
软阈值处理后的信号较为光滑，连续性好，但小波系数μj,k、wj,k存在着偏差，为一恒值，去噪后信号方差大，易使信号边缘出现模糊等失真现象。

2）硬阈值函数

其中，阈值 λ=σ 2 log N ，sign( )为符号函数，σ为噪声的标准差，median( )||w1,k为小波系数w1,k在第一层的幅值中间值。

用硬阈值处理的信号在某些点处会产生间断，使得小波系数 μj,k在 ||wj,k=λ 处不具连续性，去噪不彻底。

软阈值去噪易失真，硬阈值去噪不彻底，基于两者存在的缺点，文献［6～7］提出了两种阈值函数，去噪质量得到了提升，其函数分别为

3）函数3［6］

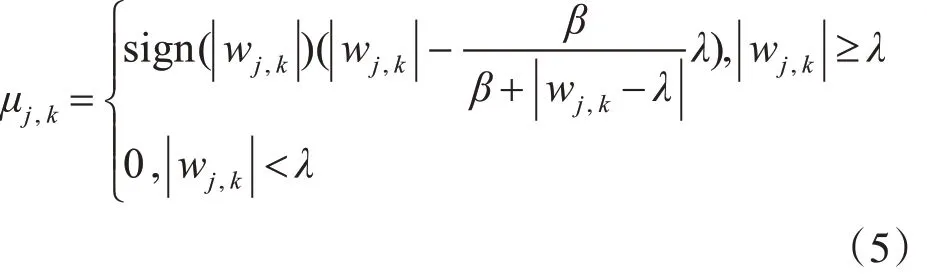
其中β 为调节因子，且为正数。

4）函数4［7］

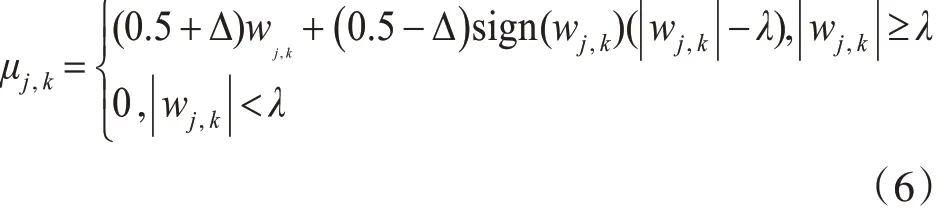
其中 Δ 为调节因子，且 -0.5 ≤Δ ≤0.5 。

函数3 中，wj,k、μj,k间不再有偏差存在，但对于小波系数中大于阈值的部分未加处理，致使小波系数 μj,k在 ||wj,k= λ 处仍不具连续性；函数 4 与之相反，μj,k在 ||wj,k=λ 处连续性好，但 wj,k，μj,k间仍有偏差影响。以上四个函数在去噪中都存在不足，针对函数3 和4，本文作了改进，提出了一种新的阈值函数。

5）函数5

其中，α、β 为调节因子，-0.5 ≤α ≤0.5，β 为正数。

（1）当 α=-0.5 ， ||wj,k=λ 时 ，μj,k=0 ，当wj,k→ λ 时，μj,k→ 0 ，可见 wj,k在 ||wj,k= λ 处具有连续性。

（2）当 α=-0.5， ||wj,k→∞ 时，μj,k→wj,k，随着wj,k的增大 μj,k也随之增大，当wj,k增大到一定程度，μj,k近似等于 wj,k，μj,k与 wj,k之间克服了偏差的问题，得到突破。

（3）当 α=-0.5 ，β →0 或是 α=0.5 时，为硬阈值函数。

（4）当 α=-0.5，β →∞时，为软阈值函数。

可见，对于新阈值函数5 来说，只需改变α、β的值就可以得到想要的阈值函数，方法灵活，较为方便实用。

本文用信噪比和均方误差作标准对去噪后的效果作对比。

信噪比公式为

均方误差公式为

其中 f(k)表示原始信号，fˆ(k)表示去噪后的信号。

4 仿真分析

接下来进行验证，选一简单的正弦信号，加入高斯白噪声，用文中的五种方法进行去噪，仿真中运用到的软件为Matlab R2010，阈值策略为“heursure”，小波基为 db3 小波，分解层次为5 层，采样点数为1024，采样频率为1000Hz，生成的仿真图见图1～2。

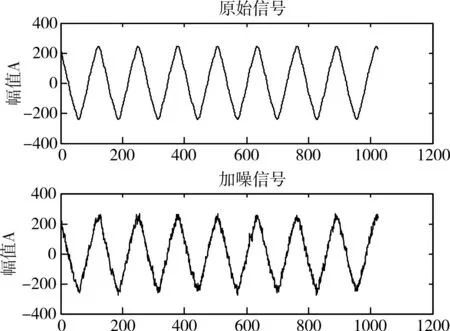
图1 原始信号及加噪信号

经过以上阈值函数去噪处理的信噪比和均方误差见表1。

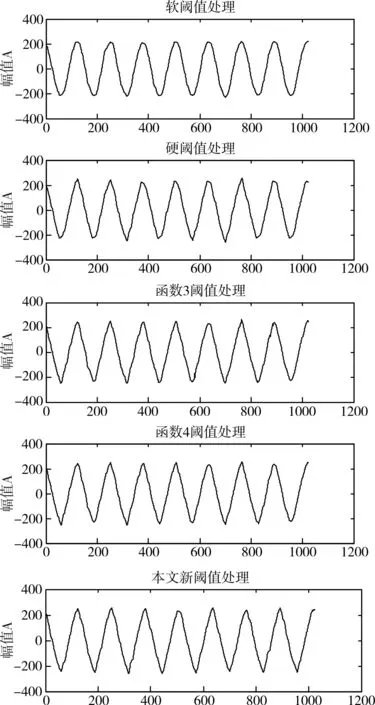
图2 不同阈值方法处理后的效果图

表1 不同函数去噪后的信噪比与均方误差

图2 是五种算法去噪后的效果图，从中看出，软阈值、函数4 和新阈值函数5 处理后的信号波形较为光滑，硬阈值和函数3 处理的信号波形中仍存在一些震荡点。从表1 数据可以看出，硬阈值和函数3 去噪处理后的MSE 值偏大、软阈值和函数4 处理后的MSE值相对偏小，新阈值函数5去噪方法与以上四种去噪方法相比优越性就突出了，无论是SNR还是MSE，数据较为理想，效果较佳。

证明了新阈值函数方法的有效性后将其运用到实际现场中，图3 是在工况现场用振动传感器采集到的振动信号，信号波形图见图3，采样点数为1000，采样频率为1000Hz。

图3 振动信号波形图

图3 振动信号中覆盖着大量的噪声信号，应用新阈值函数5 去噪，阈值策略选“heursure”，小波基选db3 小波，分解层次设为5 层，保持不变，去噪后的波形图见图4。

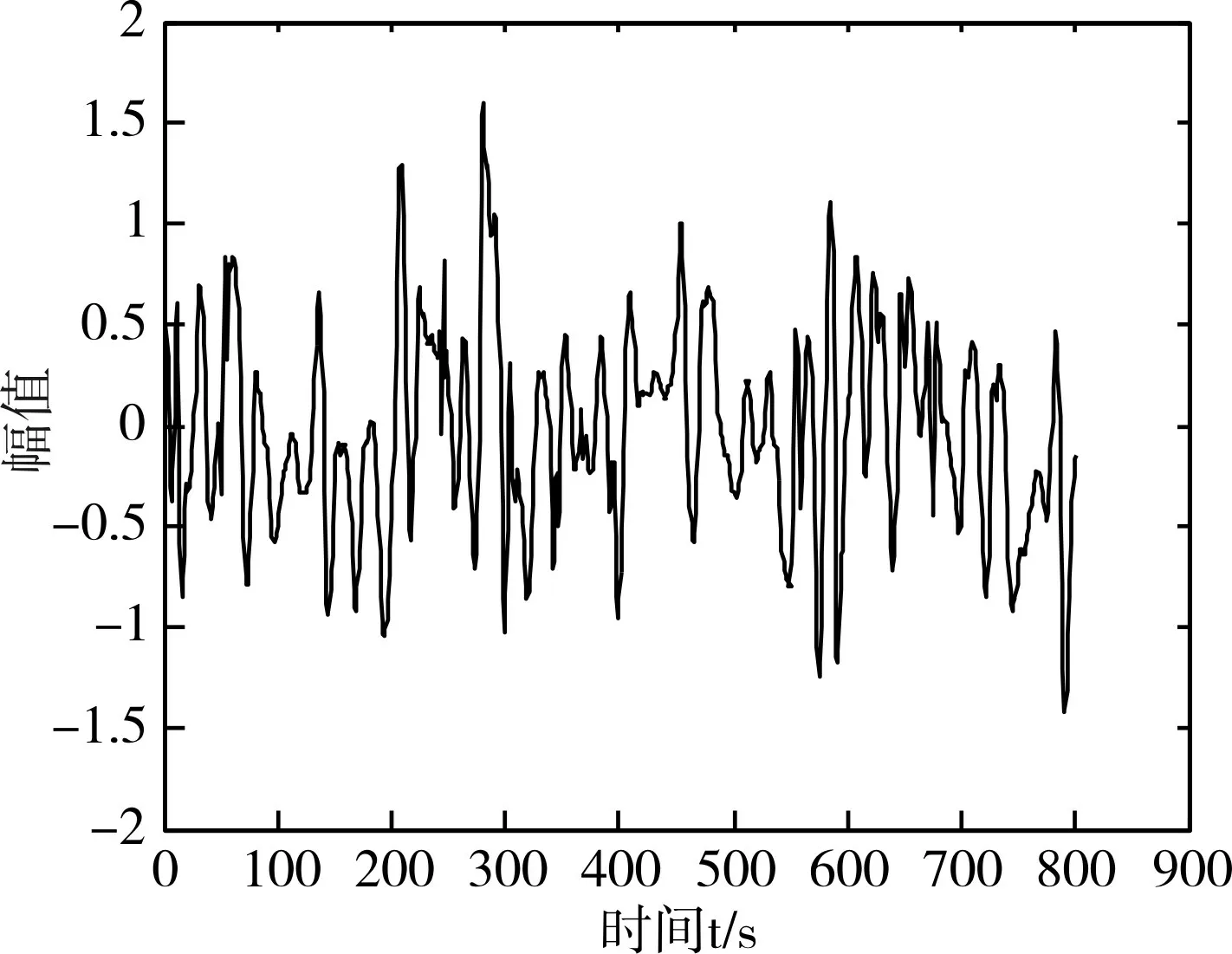
图4 小波降噪后的信号

新阈值去噪后的SNR 值为35.7166，MSE 值为0.0713，为最优值。

5 结语

阈值函数影响着重构信号的精度和连续性，选择一个合适的阈值可以极大地提高去噪质量。本文在现有的小波去噪方法的基础上进行了改造，提出了一种全新的阈值算法，并通过仿真实验作为对比，验证了新阈值算法的先进性和优越性，由此可以证明采用新的阈值函数算法去噪效果显著，实用价值高。