《对数函数及其性质》(第1课时)教学设计
曾国文

一、教材分析
对数函数是高中数学学习很重要的基本初等函数之一,学好本节内容,有助于学生加深对函数概念与性质的认识,能进一步完善对函数图像及性质的系统性认识,深化对类比、数形结合等思想方法的理解,并为学生后续学习奠定良好的基础,另外,对数函数的模型在生产生活与科学研究中有着紧密联系,对这部分知识学习有着广泛的现实意义。
二、教学目标
1.知识目标
掌握对数函数的概念、图象和性质及性质的简单应用
2.能力目标
让学生通过观察、分析、数形结合、归纳等思维活动,归纳出对数函数及其性质。
3.情感目标
让学生在探究学习的过程中,体会数形结合、分类讨论和从特殊到一般等学习数学的方法,培养识图用图的能力,培养发现问题、探究知识的学习习惯及团队合作学习的现代精神。
三、学法与教具
1.学法:观察、类比、交流、讨论、发现等;
2.教具:多媒体辅助教学。
四、重难点
重点:理解对数函数概念,掌握其图象和性质;难点:底数a对对数函数的影响和作用。
五、教学过程
1.设置情境,提出问题
对每一个碳14含量P的取值,通过对应关系,都有唯一的t与之对应,那么时间t與碳14的含量P之间的对应能否构成函数?(调动学生探索新知的欲望)
2.探索新知
课前提问:(1)在对数函数的定义中,为什么要限定a>0且a≠1?
(2)为什么对数函数y=logax(a>0且a≠1)的定义域是(0,+∞)?
答:①据指对数互化知y=logax化为ay=x,要使ay=x有意义,须规定a>0且a≠1.
②由y=logax化为x=ay,不管y取什么值,ay>0,所以x∈(0,+∞)。
【设计意图】通过提问及充分讨论、交流,加深对对数函数的含义的理解。
例1、判断下列函数是否是对数函数:
①y=2log3x;②y=log5x+1;③y=log3(2x+1);④y=logx3;⑤y=log5x2
变式1:若函数y=(a2-3a+3)
logax是对数函数,求a的值.
【设计意图】通过典例强化对对数概念的内涵与外延的理解,通过变式训练加强巩固。
下面通过图象来研究函数的性质:
先完成P81表2-3,并根据此表用描点法或用电脑画出函数y=log2x的图象,
再利用电脑软件画出y=log0.5x的图象。
注意到:y=log0.5x=-log2x,
由于(x,y)与(x,-y)关于x轴对称,因此,y=log0.5x的图象与y=log2x的图象关于x轴对称。
进一步探究:选取底数a(a>0,且a≠1)的若干不同值,在同一坐标系内作出相应的图象,通过图像观察,你能发现它们有哪些特征吗?
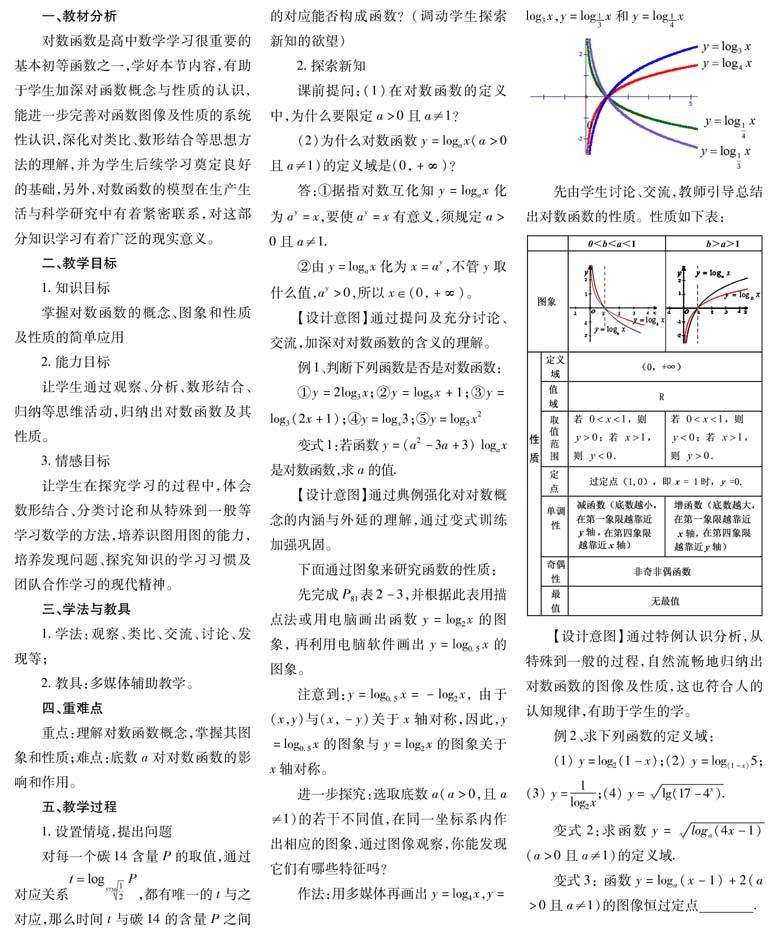
作法:用多媒体再画出y=log4x,y=log3x,y=log13x和y=log14x
先由学生讨论、交流,教师引导总结出对数函数的性质。性质如下表:
【设计意图】通过特例认识分析,从特殊到一般的过程,自然流畅地归纳出对数函数的图像及性质,这也符合人的认知规律,有助于学生的学。
例2、求下列函数的定义域:
(1) y=log2(1-x);(2) y=log(1-x)5;(3) y=1log2x;(4)
y=lg(17-4x).
变式2:求函数y=loga(4x-1)(a>0且a≠1)的定义域.
变式3:
函数y=loga(x-1)+2(a>0且a≠1)的图像恒过定点 .
【设计意图】通过典例及变式训练,强化对对数函数的图像及性质的理解和应用。
例3、比较下列各题中函数值的大小:(课本第72页例8)
(1) log23.4,log28.5;
(2) log0.31.8,log0.32.7;
(3)
loga5.1,loga5.9(a>0且a≠1);
(4) logπ3,log3π.
变式4:设a=log32,b=log52,c=log23,则a,b,c大小关系为 .
【设计意图】通过比较大小典例与变式训练,让学生灵活运用对数函数的图像及性质,也掌握了比较大小的若干方法。
例4、如图所示的曲线是对数函数y=logax,y=logbx,y=logcx,y=logdx的图像,则a,b,c,d与1的大小关系为 .
【设计意图】通过类比指数函数中这类问题的判断方法,让学生找出相应的判断方法,体会类比推理在学习中作用。
3.课后思考:①这四组对数函数y=logax与y=log1ax,y=logax与y=loga(-x),y=logax与y=-loga(-x),y=logax与y=ax(a>0且a≠1)的图像具有什么关系?
②怎样可以快速画出对数函数y=logax(a>0且a≠1)的大致图像?
【设计意图】激发学生进一步探索知识的欲望,为下一节有效学习做铺垫。
4.布置作业:
1.P74
A组第7、8题;
2.(1)求y=2+log2x(x≥1)的值域;(2)已知函数y=f(2x)的定义域为[-1,1],求函数y=f(log2x)的定义域。
【设计意图】通过作业训练,及时观察效果及发现问题,为后续学习做好更科学的教学设计。
(作者单位:福建省德化第一中学)

