表面织构对径向滑动轴承静态特性的影响

殷思明，赵三星

(武汉科技大学 机械自动化学院，武汉 430081)

滑动轴承能够承受较大的冲击载荷，因此广泛应用于各类型机器中。从环保和经济性考虑，需要以较小的功率损耗使机械正常运行。对轴承施加表面织构是提高轴承工作性能的办法之一。

国内外学者已对滑动轴承表面织构流体动压润滑进行了深入研究。文献[1-2]以数值和试验方法进行研究，结果表明，在稳定工作条件下，波浪形表面织构轴承比光滑轴承承载能力更强，摩擦力更小，运行更稳定。文献[3-4]利用理论分析研究了凹槽形微织构对径向滑动轴承的稳定性、承载力和摩擦力的影响。文献[5]利用数值仿真研究了在稳态工作条件下球形表面织构对径向滑动轴承润滑性能的影响，通过理论分析发现，与光滑表面轴承相比，部分织构使轴承最大油膜压力和摩擦力减小，最小油膜厚度增大，轴承润滑性能提高。文献[6]研究了3种形状的织构对轴承流体动压润滑的影响，结果表明长方体形织构比圆柱形和球形织构更能提升轴承性能。文献[7]分析了混合润滑状态下表面织构参数对滑动轴承润滑性能的影响，得出织构半径和深度对轴承润滑性能有重要影响。文献[8-9]发现在低偏心率时部分织构对轴承性能有明显提升，在高偏心率时全织构和部分织构都不能使轴承性能明显提升。

大多数理论研究都是采用传统Reynolds边界条件，而采用质量守恒法研究此类问题的文献较少。由于Reynolds边界条件没有遵循质量守恒原则，微织构滑动轴承的油膜往往会产生多处空穴，此时用Reynolds边界条件所得分析结果已不准确，而质量守恒算法能较为准确地预测空穴位置，更接近真实情况。鉴于此，现采用p-θ模型质量守恒法研究表面织构对滑动轴承静态性能的影响，分析凹坑半径、数目、深度和位置分布等对轴承承载能力、摩擦力、摩擦因数的影响。

1 理论分析

1.1 滑动轴承几何模型

织构化径向滑动轴承示意图如图1所示。图中：O，O1分别为轴承、轴颈中心；e为偏心距；φ为偏位角；φ1，φ2分别为周向织构起始角和终止角；c为半径间隙，c=R1-R；R1为轴承内半径；R为轴颈半径；Oc(xc,yc,zc)为椭球形织构球心；U为轴颈线速度；rx，ry，rz分别为织构在x，y，z方向上的半径，对于特殊椭球形织构，rx=rz=r，r为特殊椭球形(在φ，z面上投影为圆形)凹坑半径，ry为最大凹坑深度，椭球织构中心在轴瓦上，所以yc=0。则此椭球形凹坑深度Δh为

图1 织构化径向滑动轴承示意图

(1)

文中织构均匀分布于轴瓦上。织构化轴承展开示意图如图2所示。图中：Nt0为周向织构分布数(列数)，Ntz为轴向织构分布数(行数)。Z1，Z2为轴向织构控制参数，当φ2-φ1=2π，[Z1,Z2]=[-1,1]时为全织构；当φ2-φ1<2π或 [Z1,Z2]≠[-1,1]时为部分织构。

图2 织构化轴承展开示意图

一般椭球形凹坑织构形状方程为

(2)

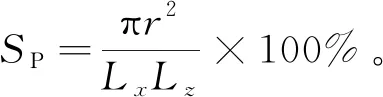
1.2 p-θ空穴分析模型

稳态工况下Reynolds方程为

(3)

式中：h为油膜厚度；p为油膜压力；η为润滑油的动力黏度。

p-θ模型引入饱和函数θ，在完整油膜区，p>pcav,令θ=1；在空穴区，p=pcav<0,令0<θ<1,pcav为空穴压力。p-θ模型滑动轴承润滑方程为[10]

(4)

该方程将完整油膜区和空穴区统一到一个方程中，满足质量守恒条件。

将参数作量纲一化处理

(5)

式中：φ为量纲一的周向坐标；Z为量纲一的轴向坐标；B为轴承宽度；H为量纲一的油膜厚度；P为量纲一的油膜压力。

p-θ模型量纲一的润滑方程为

(6)

光滑表面滑动轴承油膜厚度为

h=c+ecosφ,

(7)

织构轴承量纲一的油膜厚度为

(8)

p-θ算法边界条件为

P(φ=0,Z)=0；P(φ=2π,Z)=0；

P(φ,z=±1)=0；空穴区时,P=Pcav。

(9)

采用等距差分公式对(6)式进行离散，并用逐次超松弛迭代法对离散的代数方程组进行数值迭代求解P和θ。油膜压力收敛条件为

(10)

式中：m,n分别为周向和轴向的网格节点数；k为本次计算次数；k-1为上次计算次数。为使计算结果更精确，且考虑到计算时间不宜过长，取m=470，n=200；一般误差范围为10-4～10-6，取σ0=10-4。

1.3 滑动轴承静态特性

1.3.1 承载力

轴承量纲一的承载力为

(11)

(12)

1.3.2 摩擦力

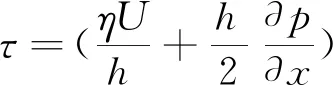
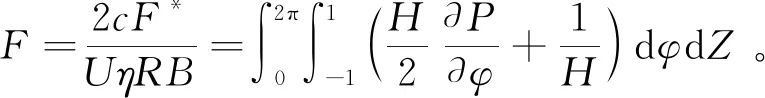
(13)

摩擦因数f为

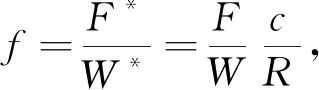
(14)

式中：W*为承载力；F*为摩擦力。

2 结果与分析

轴承参数及工况见表1。

表1 工况与几何参数

在光滑表面轴承中采用Reynolds边界条件和p-θ算法计算，距离轴承轴向中心1/5处和3/5处量纲一的油膜压力周向分布图如图3所示。由图可知，相比于Reynolds边界条件，p-θ算法的结果在不同轴向截面上更接近文献[11]的试验结果，与实际更为相符。

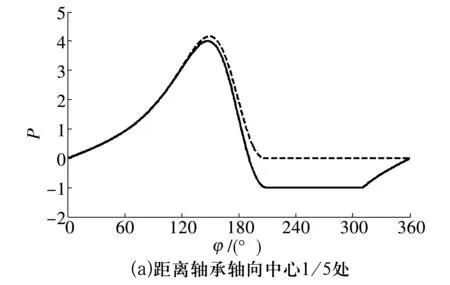
图3 光滑表面轴承Reynolds边界条件和p-θ算法下量纲一的油膜压力周向分布图

计算出上述2种算法下的承载力和偏位角见表2。由表可知，文中p-θ模型计算结果与文献[12]中不可压缩空穴模型的计算结果相比，承载力相差0.55%，偏位角相差1.14%，差别很小，验证了该算法的可靠性。

表2 光滑表面轴承静态特性对比表

现采用p-θ模型研究椭球形织构半径、数量、深度和分布位置等对径向滑动轴承的承载力、摩擦力和摩擦因数的影响。

2.1 凹坑半径和数量的影响

ry=0.11 mm,Ntz=2时织构化轴承和光滑轴承量纲一的承载力W、摩擦力F和摩擦因数f随周向织构数目Nt0变化趋势如图4所示。由图可知，Nt0一定时，随着凹坑半径r增大，织构化轴承W和F减小，f增大，且与光滑轴承W，F，f的差距逐渐增大；随着Nt0的增大，这种差距也逐渐增大。Nt0在相邻的奇、偶数变化时，W，F，f有较明显差别，这种差别随着Nt0的增大而减小。这是因为当Nt0为奇数时，轴承中心(φ=180°)位置有织构存在，对轴承中心油膜厚度及轴承性能会造成一定的影响。

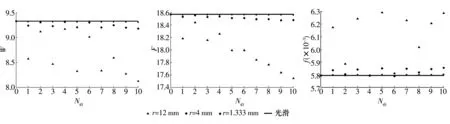
图4 织构化轴承和光滑轴承量纲一的承载力、摩擦力和摩擦因数随周向织构数目的变化情况

2.2 凹坑深度的影响

Nt0,Ntz越大，织构数目越大，对轴承性能的影响越明显，故研究凹坑深度的影响时，二者取合适的较大值。r=1.333 mm，Nt0=47，Ntz=20，Lx=Lz=6.7 mm，Sp=12.4%，不同最大凹坑深度ry下，量纲一的承载力、摩擦力和摩擦因数变化情况如图5所示。由图可知，与光滑轴承相比，全织构轴承的W，F更小，但f更大，说明全织构对轴承静态性能有消极影响;且随着ry的增大，W和F减小，f增大，全织构轴承与光滑轴承的W，F，f的差距也越来越大。因此，凹坑深度越大对轴承性能提升越不利，但考虑磨损等原因，也不能太小，故取ry=0.058 2 mm。

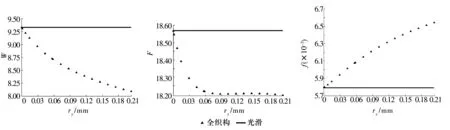
图5 量纲一的承载力、摩擦力和摩擦因数随织构最大凹坑深度变化情况

2.3 凹坑分布的影响

为了研究凹坑(r=1.333 mm，ry=0.058 2 mm)分布对滑动轴承静态特性的影响，考虑表3中的4种织构分布情况。

表3 光滑轴承和4种织构分布轴承静态性能对比表

由表3可知，情况1，2，3的承载力、摩擦力低于光滑轴承(情况0)，摩擦因数高于光滑轴承，对轴承性能有消极影响；情况4承载力高于光滑轴承，摩擦力、摩擦因数均低于光滑轴承，对轴承性能有积极影响。情况1，3偏位角高于光滑轴承，情况2偏位角低于光滑轴承，情况4偏位角与光滑轴承相等，情况2，4更稳定。4种织构分布情况下量纲一的油膜厚度如图6所示。

由图6可知，情况1为全织构，情况2织构位于轴承周向0°～180°，情况3，4织构位于周向180°～360°。结合表3可知，情况3承载力低于光滑轴承，高于情况1，2；情况4承载力(织构周向、轴向均局部分布)高于光滑轴承；情况1，2，3摩擦因数都高于光滑轴承，但是差距越来越小，情况4低于光滑轴承，所以织构周向分布在180°～360°更益于轴承性能的提升。需要指出的是，与光滑轴承相比，情况4承载力增加、摩擦因数减小不太明显，这是因为轴承偏心率(0.61)较高。

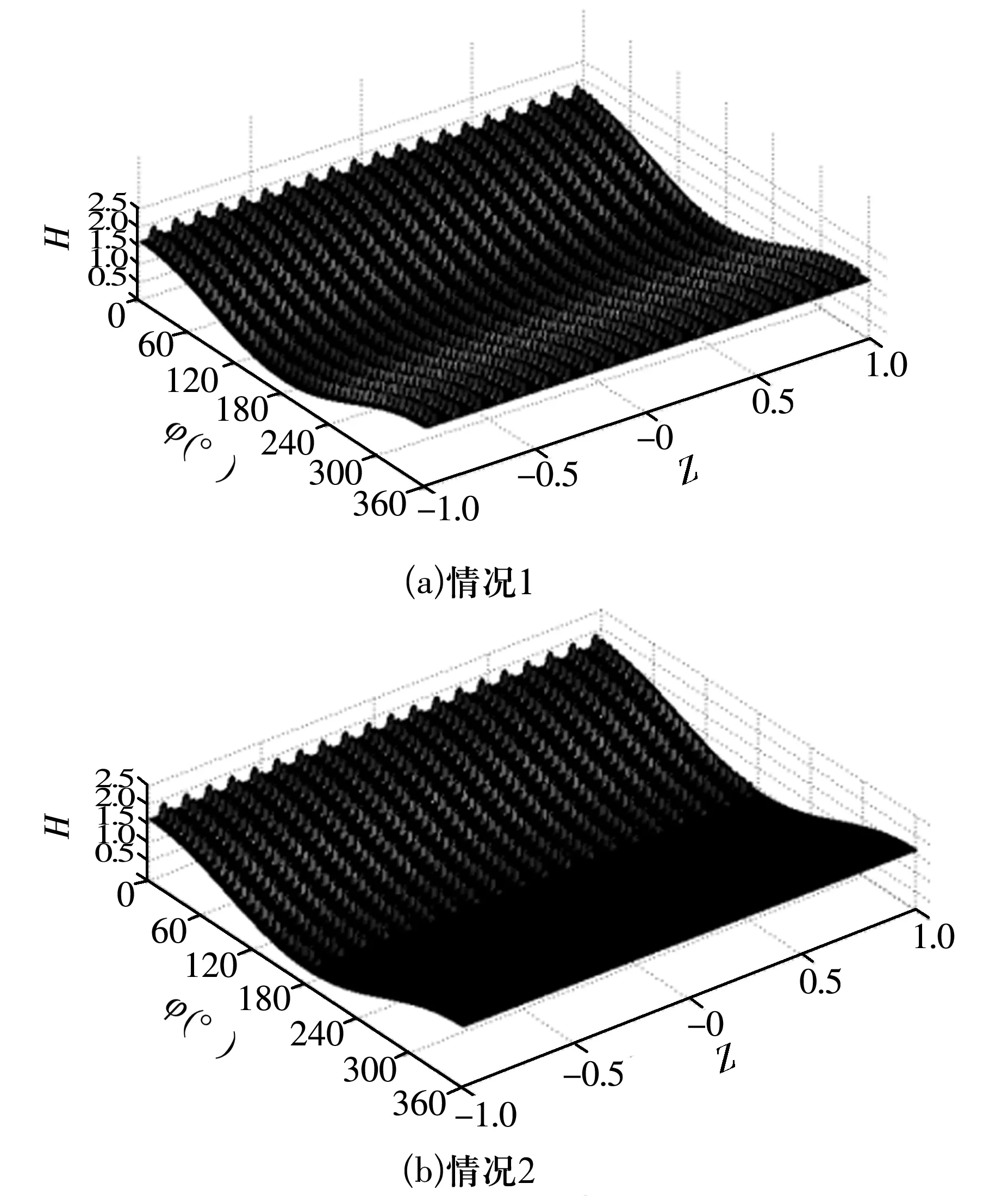
图6 4种织构分布情况下油膜厚度

3 结束语

利用p-θ模型对织构化径向滑动轴承静态特性进行分析，结果表明，椭球形凹坑半径、深度、数目、分布等都影响滑动轴承润滑性能。全织构对轴承性能有负面影响。织构周向分布在180°～360°比分布在0°～180°更有益于提升轴承性能。与光滑轴承相比，合理分布的部分织构能提升轴承性能。轴承偏心率较高，部分织构对轴承性能提升的程度不显著。轴承性能除受织构周向位置影响，还受轴向位置影响。在后续研究中需要进一步深入细致探讨这些影响参数，通过优化分析，以期得到更有效的织构分布。