圆柱滚子轴承合套参数对轴承振动特性影响分析

郑艳伟，邓四二,2，张文虎

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.辽宁重大装备制造协同创新中心，辽宁 大连 116024；3.西北工业大学 机电学院，西安 710072)

现代航空发动机主轴中多采用滚动轴承支承的转子结构，圆柱滚子轴承以优良的高速性能广泛应用于航空发动机主轴上，其振动特性直接影响主轴的整体性能。如何降低高速圆柱滚子轴承的振动已成为航空发动机主轴设计中亟待解决的关键问题。

国内外学者针对圆柱滚子轴承的振动特性以及轴承合套进行了广泛研究。文献[1]在Hertz接触理论的基础上建立了圆柱滚子轴承的动力学模型，分析了滚子承载个数对轴承振动特性的影响。文献[2]在建立圆柱滚子轴承有限元模型的基础上，研究了滚子修形对轴承振动特性的影响，证明了滚子相切圆弧修形更有利于减小轴承径向振动。文献[3]研究了滚道的不同缺陷类型、缺陷尺寸和波纹度对圆柱滚子轴承振动的影响规律。文献[4]根据非线性力学和声学理论，建立了轴承结构本身产生振动噪声的数学模型，分析了轴承结构参数对轴承振动噪声的影响，结果表明轴承径向游隙对轴承振动噪声的影响最为显著，并呈现很好的线性关系。文献[5]研究了轴承座孔偏斜误差对轴承支承刚度及转子振动特性的影响规律，结果表明：当偏斜角度增大时，在偏斜平面上系统的振幅增大且峰值位置向偏斜的一端移动。文献[6]建立了圆柱滚子轴承滚子与滚道间的润滑油Reynolds方程，分析了不同工况下由于油膜压力变化引起的圆柱滚子轴承噪声，证明轴承噪声随载荷和转速的增大而增大。文献[7]在Hertz弹性接触理论和滚动轴承运动学的基础上，分析了滚动轴承产生的变刚度振动对系统响应的影响规律。文献[8]分析了轴承零件几何误差、表面粗糙度等影响轴承振动与噪声的主要因素。文献[9]建立了滚子与滚道非理想Hertz线接触力模型，研究了圆柱滚子轴承局部故障尺寸对圆柱滚子轴承振动特性的影响规律。文献[10]研究了制造与装配误差对圆柱滚子轴承性能的影响，为滚动轴承考虑多种随机误差影响的可靠性优化设计提供借鉴。文献[11]研究了圆柱滚子轴承滚子、滚道尺寸误差对载荷分布的影响。文献[12]对球轴承合套产生噪声进行了试验分析，证明球形误差是合套后产生噪声的主要原因。文献[13]给出了轴承游隙的合套方法以及最大匹配原理，并采用VB与MATLAB混合编程实现了轴承游隙的自动选配。文献[14]对调心滚子轴承合套合格率低的问题进行了分析，证明内圈和外圈的宽度误差是影响轴承合套率的主要因素。文献[15]分析了影响深沟球轴承径向游隙的原因，证明通过控制沟道圆度、沟曲率半径偏差等可以确保合套后的径向游隙质量。文献[16]针对大型调心滚子轴承合套后游隙不稳定的问题，从合套原理、加工工艺以及检测工具进行分析，并制造了专用检测仪器，提高了合套率和生产效率，减小了产品返修率。上述研究多针对轴承内部参数对轴承振动特性的影响，而有关圆柱滚子轴承合套参数对轴承振动特性的影响分析相对匮乏。

鉴于此，在轴承动力学分析的基础上，建立圆柱滚子轴承的动力学微分方程组，分析轴承内、外滚道直径和滚子直径对轴承振动特性的影响，以期为圆柱滚子轴承合套参数的选择提供理论依据。

1 圆柱滚子轴承动力学模型

圆柱滚子轴承的保持架由外圈引导。假设轴承零件的工作表面具有理想的几何形状，其形心与质心重合。根据圆柱滚子轴承的结构特点，建立以下5种坐标系(图1)：

1)轴承惯性坐标系{O;x,y，z}，x轴与轴承转轴重合，yz面与通过轴承中心的径向平面平行,此坐标系在空间中固定不变，其他坐标系均参照此坐标系确定。

2)滚子质心坐标系{Or;xr,yr,zr}，坐标系原点Or与滚子几何中心重合，yr轴沿轴承径向方向，zr轴沿轴承周向方向，此坐标系随滚子中心移动，但不随滚子自转，每个滚子都有各自的局部坐标系。

3)保持架质心坐标系{Oc;xc,yc,zc}，由惯性坐标系平移得到，坐标原点Oc与保持架几何中心重合，随保持架移动和旋转。

4)内圈质心坐标系{Oi;xi,yi,zi}，由惯性坐标系平移得到，坐标原点Oi与内圈几何中心重合，坐标系随内圈移动和旋转。

5)保持架兜孔中心坐标系{Op;xp,yp,zp}，初始其与滚子质心坐标系重合，之后随保持架移动和旋转，坐标系原点Op与保持架兜孔几何中心重合，每个兜孔都有各自的局部坐标系。

1.1 滚子动力学微分方程组

在轴承工作过程中，滚子受到内、外滚道和保持架共同作用，其受力情况如图2所示，图中所有作用力及力矩的表达式见文献[17-18]。

,(1)

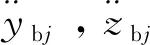
1.2 保持架动力学微分方程组

轴承在工作过程中，保持架受到滚子的碰撞力、外圈的引导力以及油/空气混合物对其端面和表面的阻力的共同作用，保持架受力如图3所示。

图3 保持架受力示意图

(2)

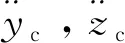
1.3 内圈动力学微分方程组

内圈的非线性动力学微分方程组为

(3)

2 轴承合套原理

根据轴承设计原理，轴承径向游隙为

Gr=De-di-2Dw，

(4)

式中：De为外滚道直径；di为内滚道直径。

轴承径向游隙的配套公式为

(5)

式中：ΔDe为外滚道直径偏差；Δdi为内滚道直径偏差；ΔDw为滚子直径偏差。

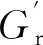
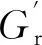
3 圆柱滚子轴承振动特性分析

以NU2307ME型圆柱滚子轴承为例，主参数及工况条件见表1。套圈、滚子材料为GCr15，保持架材料为ZCuZn40。轴承合套后的径向游隙在CN组别内，即游隙为25～50 μm[19]。合套后的游隙不在CN组内的，数据无效；在CN组内的，数据有效。采用预估-校正的GSTIFF变步长积分算法对动力学微分方程组(1)～(3)式进行求解。

表1 轴承主参数及工况条件

采用轴承振动加速度级法[19]评价轴承振动值，其中振动加速度级定义为

(6)

式中：a为某一频带范围内的轴承振动加速度均方根值；a0为参考加速度，a0=9.81×10-3m/s2。

3.1 滚道直径和滚子直径对轴承振动特性的影响

研究对象的尺寸及其偏差见表2。

表2 研究对象尺寸及其偏差

3.1.1 内滚道直径对轴承振动特性的影响

外滚道直径取70.220 mm，滚子直径取11.998 mm，内滚道直径在46.186～46.190 mm内选取，轴承合套后，径向游隙在CN组别内。

内滚道直径与轴承振动值、振动频谱的关系如图4所示，图中fvc为轴承振动基频。由图可知：随着内滚道直径的增加，圆柱滚子轴承振动值和各倍频的幅值都呈先增大后减小的趋势，当内滚道直径为46.190 mm时，轴承振动值和各倍频的幅值均最小，此时最有利于降低轴承振动。

图4 内滚道直径与轴承振动值、振动频谱关系图

3.1.2 外滚道直径对轴承振动特性的影响

内滚道直径取46.188 mm，滚子直径取11.998 mm，外滚道直径在70.216～70.224 mm内选取，轴承合套后，径向游隙均在CN组别内。

外滚道直径与轴承振动值、振动频谱的关系如图5所示。由图可知：随着外滚道直径的增加，圆柱滚子轴承振动值和各倍频的幅值都呈现增大的趋势，当外滚道直径为70.216 mm时，轴承振动值和各倍频的幅值均最小，最有利于降低轴承振动。

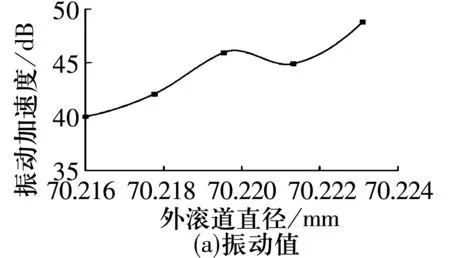
图5 外滚道直径与轴承振动值、振动频谱关系图

3.1.3 滚子直径对轴承振动特性的影响

内滚道直径取46.188 mm，外滚道直径取70.22 mm，滚子直径在11.990～12.005 mm内选取，轴承合套后，除滚子直径为11.990，12.005 mm以外，其他组径向游隙均在CN组别内。

滚子直径与轴承振动值、振动频谱的关系如图6所示。由图可知：随着滚子直径的增加，圆柱滚子轴承振动值和各倍频的幅值都呈先增大后减小的趋势，当滚子直径为12.003 mm时，轴承振动值和各倍频的幅值均最小，最有利于降低轴承振动。

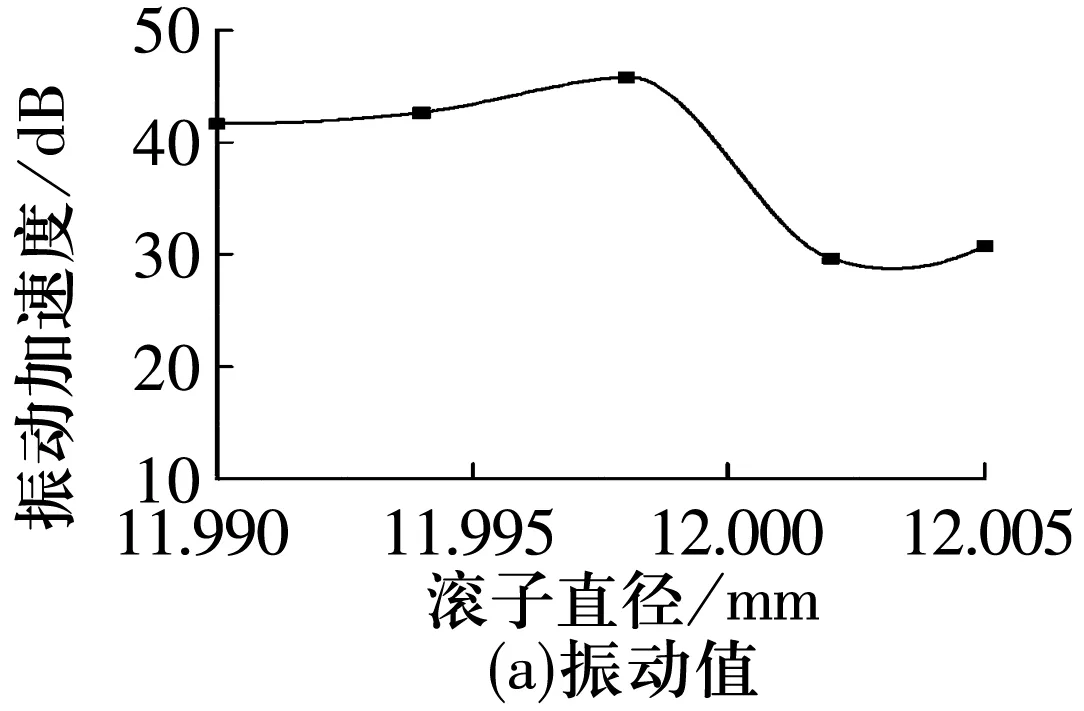
图6 滚子直径与轴承振动值、振动频谱关系图

3.2 轴承合套参数对轴承振动特性的影响

对轴承内、外滚道直径和滚子直径这3个因素进行正交优化分析[20]。内滚道直径的取值区间为46.186～46.190 mm，外滚道直径的取值区间为70.216～70.224 mm，滚子直径的取值区间为11.990～12.005 mm。采用正交算法L25(56)，进行25次试验，正交试验表见表3，其中第2，4，8，10，21，23次试验合套后的游隙不在CN组别内，故数据无效。正交试验下的轴承振动频谱、振动值如图7、图8所示。

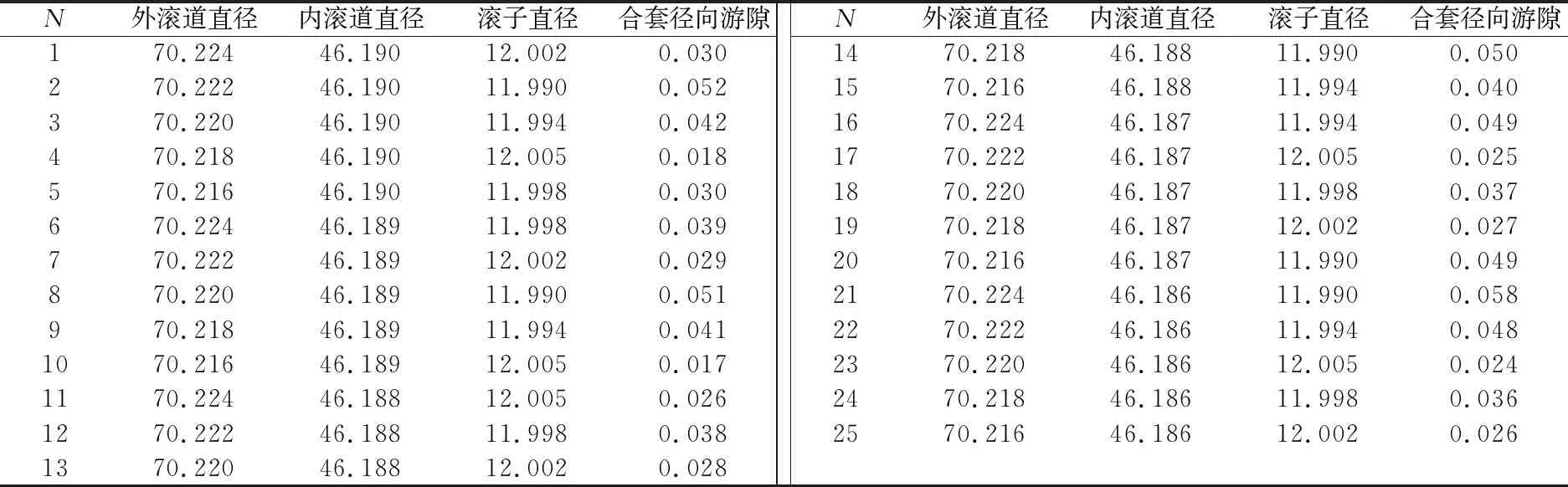
表3 正交试验表

图7 正交试验下的轴承振动频谱图

图8 正交试验下的轴承振动值

由图7和图8可知：在25次试验中，第11，13，17，19，25次试验的轴承振动值和各倍频幅值较小，且合套后的游隙均在CN组别内。利用正交表进行25次试验是为了找到对轴承振动值影响最大的参数以及各参数对轴承振动值影响程度的顺序，最后得出最佳参数组合。各参数对轴承振动值影响数据分析见表4。

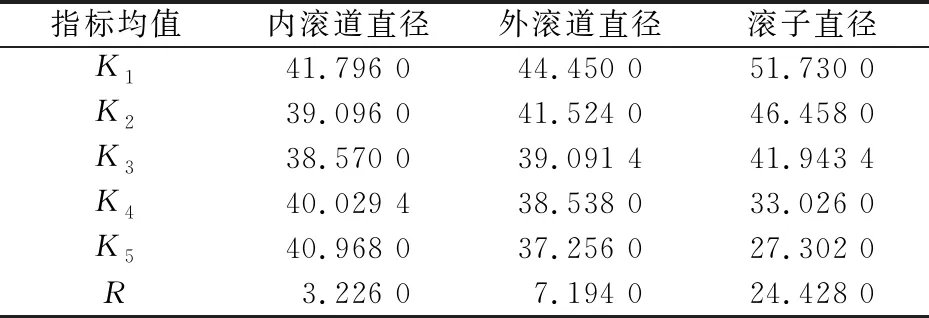
表4 各参数对轴承振动值的影响

3.3 滚道直径和滚子直径推荐选配尺寸

对比图4—图6可知，单个因素对轴承振动的影响不能反映轴承参数合套后对其振动的影响。故依据正交优化算法，推荐低振动值下的滚道直径和滚子直径尺寸，见表5。结合表3可知，在确保满足CN组合套游隙下，合套后的游隙较小时，轴承振动值较低。

表5 低振动值下的滚道直径和滚子直径

4 结论

1)圆柱滚子轴承合套参数满足CN组条件下，随着内滚道直径的增加，圆柱滚子轴承振动值和各倍频的幅值均呈先增大后减小的趋势，当内滚道直径为46.190 mm时，轴承振动值和各倍频的幅值均最小。

2)圆柱滚子轴承合套参数满足CN组条件下，随着外滚道直径的增加，圆柱滚子轴承振动值和各倍频的幅值均呈现增大的趋势，当外滚道直径为70.216 mm时，轴承振动值和各倍频的幅值均最小。

3)圆柱滚子轴承合套参数满足CN组条件下，随着滚子直径的增加，圆柱滚子轴承振动值和各倍频的幅值均呈先增大后减小的趋势，当滚子直径为12.003 mm时，轴承振动值和各倍频的幅值均最小。

4)圆柱滚子轴承合套参数满足CN组条件下，基于正交试验和极差分析法可知：滚子直径对轴承径向振动影响最大，外滚道直径次之，内滚道直径影响最小。说明轴承合套原则应先选定滚子和外圈的尺寸参数，再选择内圈参数进行合套。