表面织构在滚动轴承系统中的摩擦学分析
张迪
(上海建桥学院 机电学院,上海 201306)
表面织构技术是利用物理或化学的方法人为地在摩擦副表面加工出按一定规则分布的微几何特征[1]。这些微几何特征(微坑或微沟槽)能够作为微储油池存储润滑油。当摩擦副处于贫油润滑时,将向摩擦副表面提供润滑油,缓解贫油润滑状态[2];当摩擦副处于富油润滑时,可以产生附加流体动压力,进而提升动压承载力,有效避免摩擦副表面直接接触,从而减小摩擦[3]。此外,表面织构也可以容纳磨粒,降低由磨粒产生的高磨损[4]。表面织构是一种重要的改进润滑和减少摩擦的手段,已在全球范围内获得了广泛关注[2, 5-6]。
在油润滑下运行的滚动轴承常处于边界/混合润滑状态,不同润滑状态下表面织构技术具有不同的效果。文献[7]首先发现采用随机分布的凹坑型织构能够提升处于混合/边界润滑下的滚动轴承的寿命。文献[8]采用其输入数据进行了数值分析,探究了表面织构影响滚动轴承疲劳寿命的原因。然而,目前织构化滚动轴承的研究工作尚少,有必要研究表面织构在提升滚动轴承系统性能方面的潜力。
鉴于此,现建立滚动轴承的数值模型,采用数值分析方法,探究表面织构在滚动轴承中的应用效果。
1 理论模型
1.1 平衡方程
以内燃机用某滚针轴承为研究对象进行模拟。由于滚针轴承的有效长度较大,滚针/外圈摩擦学系统的润滑问题可视为一维线接触弹流润滑问题。滚针/外圈摩擦副示意图如图1所示。图中:n为内圈转速;nr为滚针的自转转速;Re为外滚道的曲率半径;Rr为滚针的曲率半径;Rer为当量曲率半径;u1,u2分别为摩擦副上、下表面的速度。滚针与外圈之间的间隙为
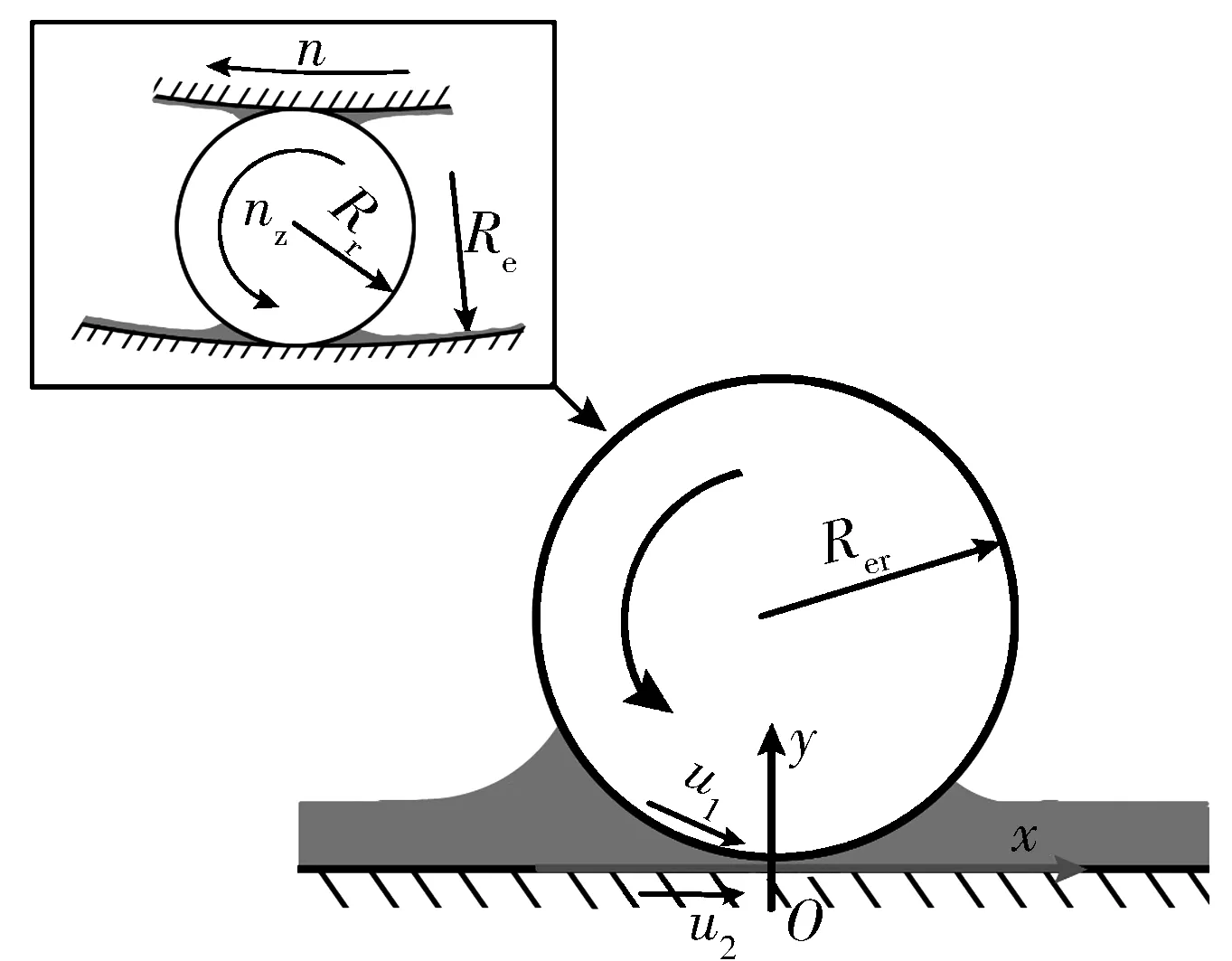
图1 滚针/外圈摩擦副示意图
(1)
式中:h0为最小油膜厚度;v(x)为各点在垂直方向上的弹性位移。
当在外圈应用激光方式加工微凹槽表面织构时(织构特征均匀分布在外圈滚道表面),滚针与织构化轴承外圈之间的油膜厚度为
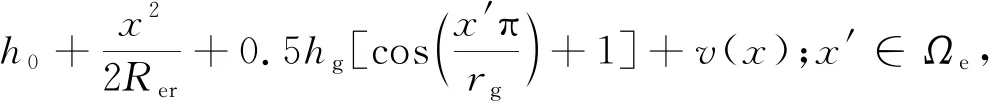
(2)
式中:hg为织构特征深度;rg为织构特征宽度的一半;x′位于局部坐标系中,其原点位于织构特征的中心[1];Ωe为织构特征所占面积。
滚针与滚道之间作纯滚动,滚针的自转转速为[9]109
(3)
滚针的公转转速为[9]109
(4)
根据流体动压润滑理论,通过求解Reynolds方程可以确定油膜厚度与油膜压力的关系。在平面摩擦副中,理想光滑状态下两相对运动表面之间的润滑膜无法产生流体动压承载力。欲使摩擦副表面之间的润滑膜产生流体动压承载力,除两表面应具有相对运动速度外,还要求沿运动方向上存在一定的收敛间隙。在滚针/外圈摩擦副中,存在着收敛-发散间隙。因此,计算油膜压力分布需采用如下方程[10]2
(5)
(6)
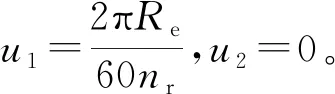
当流体压力大于空穴压力(即p>0)时,设θ=0;当空穴发生时,流体压力等于空穴压力(即p=0),θ>0,其值在0~1内。
酒店使用社交媒体营销的目的。调查结果显示:社交媒体营销人员使用社交媒体营销时,最关注的是提高品牌知名度、提供产品信息和了解消费者需求。超过一半的酒店媒体高管认为社交媒体不应成为酒店创收的工具,而应成为酒店产品信息的宣传窗口。此外,有4家酒店提到招聘员工是他们使用社交媒体的另一目的。
1.2 润滑油属性
润滑油黏度对摩擦系统的油膜压力和摩擦功耗有重要的影响,其随着温度及剪切率的改变而变化。内燃机常采用多级发动机油进行润滑。多级润滑油常使用高分子量的聚合物作为添加剂,是典型的剪切稀化流体。剪切稀化效应会引起添加剂长链分子发生剪切破坏,润滑油黏度会随剪切率的增加而减小。所以,在润滑系统的分析中有必要考虑油膜温度和剪切率对润滑油黏度的影响。
1.2.1 黏压和黏温效应
影响润滑油黏度最重要的因素是润滑油压力和温度。润滑油黏度与润滑油温度、压力的关系为
μ=μ0exp{(lnμ0+9.67)[(1+
5.1×10-9p)a]-1},
(7)
式中:T为润滑油温度;a0,T1,T2均为修正参数;a与润滑油属性相关,通常取0.68[9]10。该公式结合了Vogel的黏温公式[12]和Roelands的黏压公式[13]。
1.2.2 剪切稀化效应
润滑油黏度受剪切稀化效应影响,剪切率与润滑油黏度的关系可以用Cross公式表示[14]111
(8)
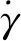
润滑油密度随润滑油压力和温度的变化而变化。通过(9)式可以获得润滑油密度随着润滑油压力和温度变化的关系为[15]
(9)
式中:ρ0为大气压下温度T0时的润滑油密度;βT为润滑油的温度扩张系数。润滑油牌号为5W30,其参数见表1。

表1 5W30润滑油参数
1.3 弹性变形
模拟分析中需要考虑表面弹性变形。根据弹性理论可推导出各点沿垂直方向的弹性位移为[16]19
(10)
式中:p(s)为载荷分布函数,对于弹流润滑问题,p(s)为流体压力分布;s为x轴上的附加坐标,表示p(s)与坐标原点的距离;s1和s2分别为载荷的起点和终点坐标;c为待定常数,通常可以并入h0中;E为当量弹性模量;Ee为外滚道的弹性模量;Er为滚针的弹性模量;νe为外滚道的泊松比;νr为滚针的泊松比。
2 模拟分析
2.1 计算流程
数值计算的模拟流程图如图2所示。(5)式属于椭圆型偏微分方程,无法用解析法求得其精确解。有限体积法具有积分守恒的特点,而且在处理润滑计算时效率较高,在质量守恒的润滑模型计算中应用最为普遍,因此采用有限体积法对(5)式进行离散。
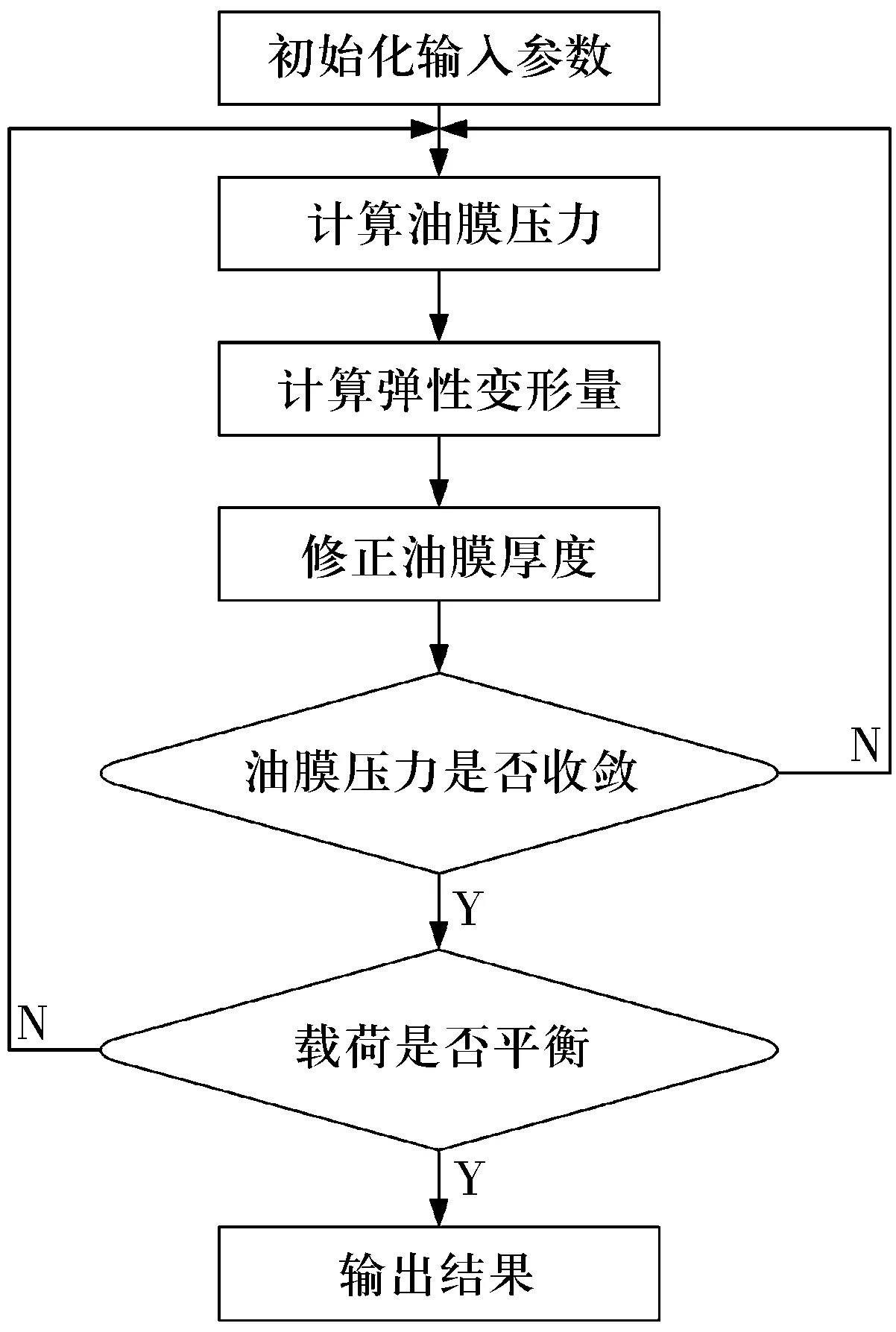
图2 模拟流程图
首先对求解域进行等距网格划分。在x方向有n个节点,网格点在x方向上的坐标为i。p(i)为在网格点i上的流体压力。有限体积法的基本思想是在特定控制体积中应用质量守恒。基于压力梯度和每个控制体积的积分,(5)式可以离散为
(11)
为了清晰起见,下标P,E,W,e和w分别用于取代下标(i),(i+1),(i-1),(i+0.5)和(i-0.5)[17]。采用文献[17]中的节点方案更适合计算下标为e和w的参数。在中节点方案中,下标为e和w的参数值是2个相邻节点处参数值的算术平均值。此外,(11)式中右端项应使用迎风格式进行离散。当采用2阶迎风格式时,整个离散的公式具有2阶精度,引入1阶迎风格式仅具有1阶精度。离散后的方程为
12Us[(1-θW)ρWhW-(1-θP)ρPhP],
(12)
he=0.5(hE+hP),hW=0.5(hW+hP),
ρe=0.5(ρE+ρP),ρW=0.5(ρW+ρP),
μe=0.5(μE+μP),μW=0.5(μW+μP)。
对(12)式进行重新排列可得
AWPW+APPP+AEPE+BPθP+BWθW+CP=0。
(13)
(13)式描述了p和θ之间的线性关系。因此,离散化后的润滑模型是一个代数方程组,其表达式为
G(p,θ)=Ap+Bθ+c=0,
(14)
式中:A为收集了Ap,AW,AE信息的矩阵;B为收集了BW和BP信息的矩阵;c为收集了边界条件和CP信息的向量集。
为了提高润滑模型求解的稳定性和收敛性,采用FBNS的方法求解润滑模型[16]。通过该方法,润滑模型的求解从有约束问题转换成无约束问题[11],而无约束问题的求解可以借助商用直接求解器进行快速求解。
2.2 模型验证
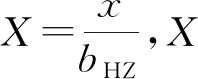
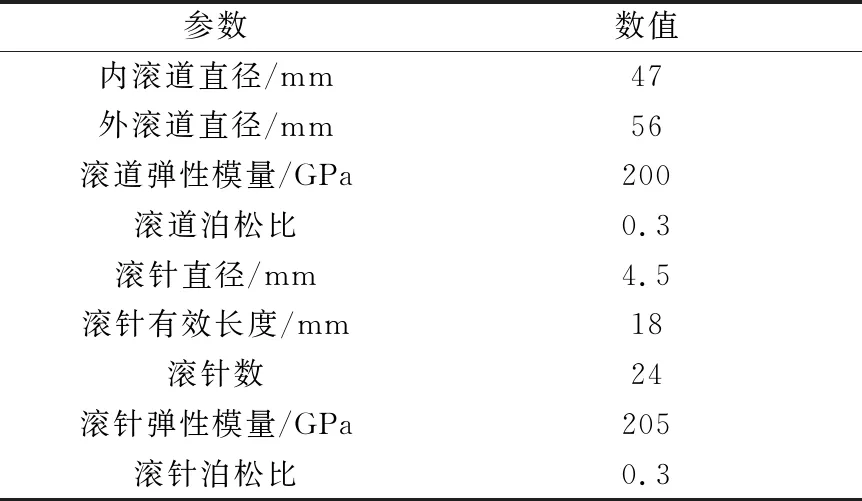
表2 滚动轴承参数
为了验证本模型的正确性,将模型的计算结果与文献[16]74的计算结果进行对比,模拟条件与该文献一致。数值模拟的结果对比如图3所示。由图可知,当前模型的计算结果与文献[16]的计算结果在压力峰值上仅存在0.5%的偏差,说明当前模型的正确性。
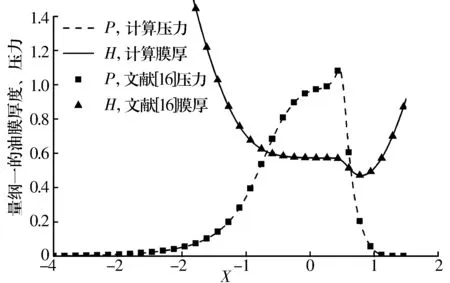
图3 弹流润滑膜厚与压力分布对比
3 结果与分析
转速分别为1 000,2 000,6 000 r/min时,有无织构下油膜厚度和油膜压力分布曲线如图4所示。虽然滚针轴承很少能适应6 000 r/min的高转速,但是研究表面织构在高转速下的性能仍具有重要的意义。
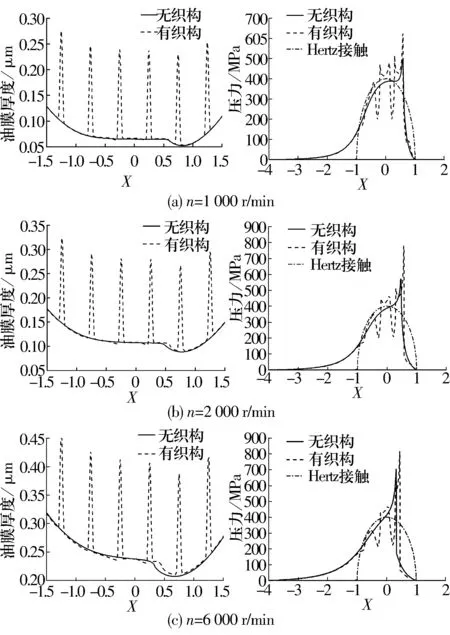
图4 外圈上有无织构时油膜厚度和流体压力分布曲
由图4可知,相比于非织构系统,织构系统的最小油膜厚度均有所增加,增量分别为1.338%,2.219%,1.612%,增量随转速的增加呈先增大后减少的趋势。最小油膜厚度的提高可以有效避免摩擦副表面的直接接触,减少摩擦副的磨损,进而提高摩擦副的摩擦学性能。不同转速使摩擦学性能的提升效果不同。在润滑区中部,油膜呈近似平行状;在润滑油出口区,油膜开始收缩,形成颈缩现象,这是线接触稳态弹流的典型特征。表面织构的存在会轻微影响颈缩位置,从而影响最小油膜厚度。此外,在润滑区中部,油膜压力分布与Hertz接触压力分布近似;在颈缩位置处,油膜压力出现明显的二次压力峰值。表面织构的存在影响流体压力分布,从而显著影响二次压力峰值。
事实上,滚动轴承的摩擦学问题属于非共形接触问题。相对于共形接触,在非共形接触中应用表面织构还存在着较大地争议[18]。前人的试验结果和数值模拟研究表明:采用合适的表面织构可以对弹流接触区的润滑效果产生有利的影响,增加处于滚动/滑动下摩擦副的局部/平均油膜厚度[2]4。同时,弹流润滑研究表明:当表面织构的尺寸小于Hertz接触尺寸时,表面织构具有积极的效果[19-22];当表面织构尺寸大于等于Hertz接触尺寸时,表面织构具有消极的效果[23-25],如凸点接触面积小,接触应力大,导致变形、烧黏、磨损及振动噪声增大等。因此,在滚动轴承应用表面织构应综合考虑各个因素。
4 结束语
为了研究表面织构在提升滚动轴承系统性能方面的潜力,以滚针/外圈作为研究对象,建立了滚针轴承系统的弹流润滑模型,探究了表面织构在不同转速下的润滑效果。研究表明:在滚针/外圈摩擦副中,采用合适的表面织构可以有效提升摩擦副的最小油膜厚度,避免摩擦副表面的直接接触,提高摩擦副的摩擦学性能。不同转速会使轴承摩擦学性能的提升效果不同。
由于模拟中所采用的恒定载荷、恒定转速的计算模型是相对简单的理论模型,故研究存在一定的局限性。研究表面织构对滚动轴承性能的影响应考虑滚动轴承的实际工况,需要建立更完善的理论模型。

