考虑涡流效应的磁悬浮转子非线性振动分析

刘学平，朱戡

(清华大学深圳研究生院 先进制造学部，广东 深圳 518000)

磁悬浮轴承(Active Magnetic Bearing，AMB)可以提供非接触式支承力，调节刚度和阻尼，具有无机械摩擦力,转速高,温升小等优点。由于电磁轴承中电磁力的非线性，往往需要将其线性化以便于控制。文献[1]最早提出线性化模型，利用一对差动电磁铁构造出近似的线性力-电流模型。为了避免该模型局部线性化的问题，其他线性化方法也被陆续提出[2-3]。

磁泄漏、裂纹转子、转子与定子的碰摩运动都会导致非线性响应。在磁场分析方面，文献[4]研究了在轴向电磁轴承中，随着气隙间距的变化磁泄漏对电磁力的影响。在转子的碰摩分析方面，文献[5]研究了磁悬浮轴承中转子与保护轴承接触的各个方面，并且介绍了相关的控制方法。

传统文化中隐藏着中华精神和灵魂。随着国学的普及和发展，传统文化的价值日益被现代中国人所接受和认可。语文教学中渗透传统文化，可以提升学生的道德品质和民族自豪感，有助于身心的修养和完善，并帮助学生树立中国人特有的认识世界和理解世界的观念，做一名热爱祖国热爱人民的好学生。

在电磁力所引发的非线性问题上，文献[6]考察了在非线性电磁力作用下，几何耦合参数对磁轴承柔性转子运动的影响，发现当参数较大时系统存在明显的分岔、次同步谐振等非线性现象。文献[7]对磁悬浮轴承的分岔行为进行了分析，并用Lyapunov第一定理分析了系统的稳定性，发现系统中存在广泛的分岔、跳跃、多值响应和较大的初值敏感性。文献[8]考察了磁悬浮支承柔性转子的非线性振动，研究了转子的连续性和电磁力的非线性，发现了非线性模态下的内共振现象。文献[9-10]分析了在不同参数激励下拥有时变刚度的电磁轴承的动力学响应，考察了转子的响应情况，发现转子非线性响应较丰富。文献[11]利用多尺度方法计算了具有时变刚度的磁悬浮轴承的瞬态和稳态响应。文献[12]考察了存在转子角度偏移的电磁轴承的非线性动力学响应，发现随着几何参数的变化，系统产生了大量的次同步谐振、准周期和混沌现象。文献[13]考察了存在时变刚度和几何耦合的磁悬浮轴承，并且利用非线性PD控制推迟了分岔发生的时间点，提高了转子的响应性能。

目前的研究大多集中在电磁力固有非线性导致的轴承刚度及阻尼非线性对磁轴承行为的影响，较少关注涡流产生的非线性对磁轴承的影响。因此，现考虑涡流效应对电磁力的影响，建立磁悬浮转子的动力学模型，分析转子的频率响应。

1 磁悬浮转子模型

1.1 考虑涡流的电磁力模型

磁悬浮轴承原理如图1所示。图中：u为电磁铁的端电压;i为电磁铁线圈电流;a,b分别为铁芯宽度和厚度的一半;l为磁路长度;s为气隙总长度。

新零售不再受空间时间束缚，去边界化特征。新零售的兴起打破了传统零售业基于时间和空间的经营逻辑，不断被削弱营业时间、经营范围、业态区域等对消费者的控制力，消费品受品种、数量、形态的限制也越来越低，消费体验和商品交换活动逐渐呈现出无边界性。

图1 磁悬浮轴承原理图

当电流按照正弦规律变化时，其产生的磁场强度H满足

(1)

式中：σ，μ分别为铁芯的电导率和磁导率。利用Laplace变换，设H=H0esjt，sj为Laplace变量，则(1)式变为

(2)

磁感应强度B与磁场强度H之间的关系为

B=μH，

(3)

由此可得磁感应强度空间分布为

(4)

式中：B0为铁芯中心处的磁感应强度。

磁通量φ与磁感应强度的关系为

φ=B0A，

(5)

由此可得

(6)

式中：A为铁芯的横截面积,A=4ab。

利用磁路法，可知磁感应强度B0和线圈匝数N、电流i、磁路总长度l(x)满足如下关系

(7)

式中：s(x)为气隙总长度；μ0为真空磁导率；μr为铁磁导率，μr≫1；lfe为铁芯气路长度。

将以上参数代入原方程，并联合(14)～(17)式，经化简可得

(7)式可化简为

(8)

结合(6)，(8)式，系统的磁通量与线圈电流满足以下频域关系

(9)

将(9)式进行级数展开，并保留主要的一次项，可得

本文的KBE系统集成技术包括知识集成和系统集成。KBE系统与之前的传统专家系统相比在产品设计时更加偏重于知识集成，可以实现在产品设计过程中，充分调动和利用各种知识资源；系统集成方式将KBE系统集成到CAD系统，增加KBE系统的功能，使其变得更加完善。NX系统为KBE系统提供了一个可视化环境，能够利用面向对象语言对设计的三维模型进行建立和修改，利用数据库和电子表格来存储知识信息，以及编辑Dfa文件实现知识的传递和规则库的建立。本文为了方便实现知识的集成，采用统一数据库，不需要知识数据的转换，将知识管理系统集成到NX系统中，实现知识库中数据的添加、删除和更新以及KF模块知识的获取。

(10)

(10)式即磁通量与线圈电流在频域中的关系式,为了便于分析，将其转换为时域表达式

(11)

由此可知，除了电流项以外，磁通量还与电流的微分项有关。

通常电磁轴承中采用差动模式，作用在转子上的电磁力可以表示为位移和电流的函数[1]4，即

纸浆洗涤过程并非一个稳态的模型就能准确地辨识，要用一个动态变化的模型逼近纸浆洗涤过程，前述研究中采用了神经网络的两步辨识法得到纸浆洗涤模型。两步辨识法：①采集大量的动态数据为样本，训练多输入的神经网络，通过训练好的神经网络辨识动态生产过程；②以此动态神经网络生成的大量样本数据为稳态模型的样本，训练只有主导输入的稳态模型，训练好的神经网络可稳定模拟生产过程的稳态特性。

(12)

式中：x为转子位移。

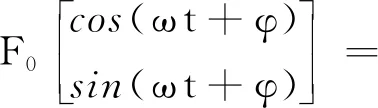
图1中磁悬浮轴承的电磁力为

(13)

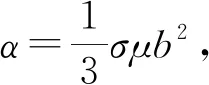
(14)

1.2 转子动力学模型

转子的动力学模型为

(15)

式中：x，y为转子的径向位移;转子受力除了重力mg(g=9.8 m/s2)外，还包括转子质量不平衡所导致的不平衡力Fw和电磁铁施加的电磁力Fs。

细菌培养基：称量牛肉膏1.5 g、蛋白胨3.0 g、NaCl 1.5 g、琼脂6.0 g，再加入清水300 mL煮沸，调节pH7.0。

(16)

式中：F0为转子所受偏心力；md为转子的不平衡质量；ω为转子转速；e为转子偏心量；φ为初始相位角。

当采用比例-微分(PD)控制时，需要建立关于电流的模型，即

(17)

为便于分析，将转子方程中参数作量纲一化处理，即

式中：kP为比例控制系数；kD为微分控制系数；ωn为转子的固有频率；t为时间。

学术界认为，无论是在理念上倡导人类命运共同体意识，还是在实践上构建人类命运共同体，并不意味着其已成为当代世界的事实判断[47]，还要准确认识其面临的诸多困境。

2.4 两组咳嗽缓解及消失时间比较 治疗后，B组的咳嗽缓解时间与咳嗽消失时间均短于A组，差异均有统计学意义(P<0.05)。见表3。

中粮宁夏年产2万t葡萄酒及配套种植基地项目区生活用水为从事葡萄酒生产101名工作人员生活用水。考虑到企业生产规模现阶段无增加的计划，因此不考虑项目区人口增加。

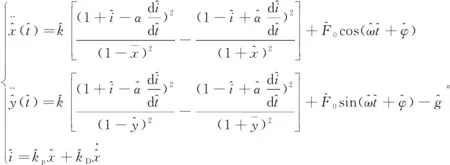
(18)

磁悬浮轴承参数见表1，将其量纲一化并代入(18)式，可得磁悬浮轴承的非线性动力学方程。

表1 磁悬浮轴承参数

2 数值计算结果与分析

(18)式是二阶非线性微分方程组，利用Runge-Kutta法可以计算得到转子的位移响应。利用MATLAB软件分析涡流参数对转子的主共振与谐振响应的影响。

当前跨境电商企业最希望招聘的是跨境电商专业对口的人才，但是由于目前鲜有院校专门开设该专业，因此，企业选择毕业生最多的专业主要是国际贸易74%，电子商务61%，和商务英语45%。

2.1 涡流效应对转子主共振响应的影响

不同偏心力下，转子在共振频率附近的最大振幅随涡流因子变化曲线如图3所示。由图可知，转子的最大振幅随偏心力的增大而增大；在同一偏心力下，涡流因子越大，转子的最大振幅越大。

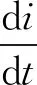
由上海市高等学校图书情报工作委员会、上海市图书馆学会、中国索引学会共同主办，上海师范大学图书馆、湖北三新文化传媒有限公司三新研究院、江苏中杨数据科技有限公司共同承办的2018“图书馆学术论坛”，今天在上海师范大学顺利召开。在此，我谨代表上海市高校图工委和相关主办、承办单位，对各位领导、专家学者及与会代表的到来表示热烈的欢迎！

图2 不同模型下的频响曲线

随着我国的企业的发展和创新，企业的治理结构也在紧随市场形势进行优化，从当前公司治理结构来透视企业财务管理目标。暴露出企业很多发展问题，因此在新形势企业在做好创新和改革的同时，也要积极强化自身内部的人才储备。选择专业素质高、文化素质强、领导能力高的人员担任公司的管理层，不仅可以为企业的发展注入新鲜血液，同时最大限度地提升企业的人才竞争力。对其企业治理结构的升级和财务管理目标的实现都具有重要意义。

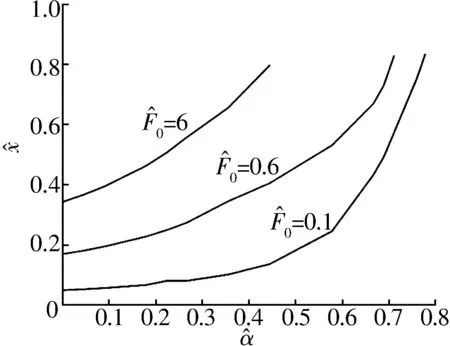
图3 不同偏心力下转子振幅随涡流因子的变化曲线

综上可知，涡流效应会增强磁悬浮轴承中电磁力的非线性，一方面会使电磁力的“软弹簧”效应更加严重，使主共振的“左偏”现象更突出，甚至出现“跳跃”现象；另一方面，涡流效应会使转子在主共振点处的振幅进一步增大，该现象在较大偏心力下更加明显。

2.2 涡流效应对转子超谐振和次谐振响应的影响

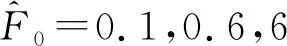
3.4.2 直流电源自身具有完善的蓄电池管理功能，可对蓄电池进行充放电管理，能有效延长蓄电池使用寿命，减少站点蓄电池投资和维护费用。

图不同涡流因子下转子位移功率谱

图不同涡流因子下转子位移功率谱

图不同涡流因子下转子位移功率谱

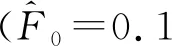
汪安南：在2013年年初召开的全国水利厅局长会议和水利规划计划工作视频会议上，陈雷部长深刻剖析和阐释了水利工作面临的新形势、新机遇和新要求，对做好新形势下水利规划计划工作指明了方向。规划计划司切实贯彻落实中央要求和部党组决策部署，重点开展了以下工作：

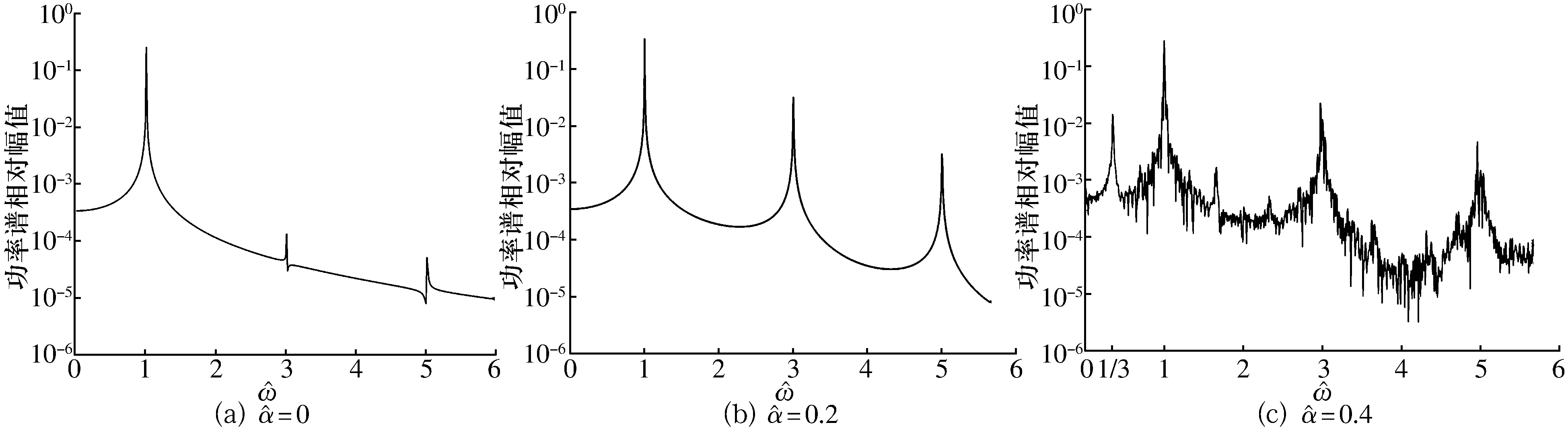
3 试验结果对比

由于涡流效应的结果表现为系统动力学方程中增加的电流微分项，因此，若已知电流微分项对转子运动的影响，就可得到涡流效应对转子运动的影响。关于磁悬浮轴承中电流增加微分项后对转子运动的影响，文献[15]进行了试验，结果如图7所示。由图7a可知，存在涡流非线性的情况下，磁悬浮轴承的转子频响曲线出现了跳跃现象，试验结果与理论分析结果(图2b)相似；由图7b可知，转子振动位移的频谱同样出现了多种倍频成分，与理论分析结果也相似。

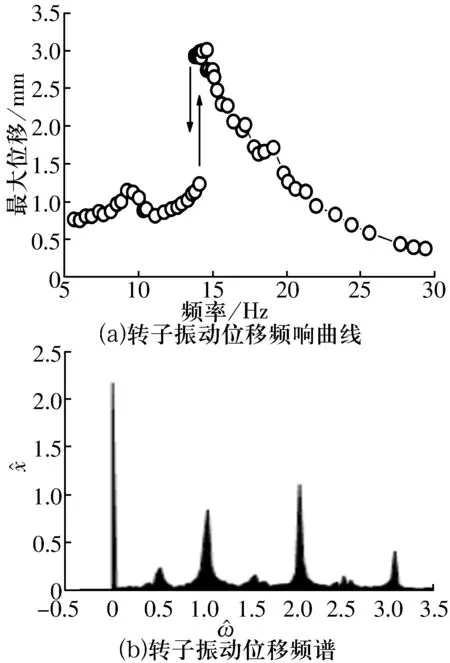
图7 试验结果

由此可知：由涡流效应产生的电流微分项对系统运动产生了明显影响，该微分项使频响曲线出现了跳跃现象，也使转子位移频谱里出现了多种倍频成分。

4 结论

考虑涡流效应对电磁力的影响，建立了电磁力的时域模型，利用Runge-Kutta法计算了磁悬浮转子振幅，得到以下结论：

1)涡流效应会引起磁悬浮轴承中电磁力的变化，使得电磁力模型中包含了关于电流的微分项，从而进一步加强了电磁力的非线性。

2)涡流效应会引起转子的频响曲线主共振区的变化，使得共振点左移，频响曲线左偏甚至出现“跳跃”现象，还会增大转子在共振区的振幅。

3)涡流效应会对转子的超谐波和次谐波响应产生影响。涡流效应使转子振幅频谱中的频率成分增加，除了主共振以外，还会产生超谐波与次谐波频率成分，并且增大谐振频率的响应幅值。