巧构造 妙解题——中考复习之一道质检题的教学思考

福建省泉州外国语学校 黄全伟

临近中考，各地质检纷至沓来，质检卷在揣摩中考动向的同时，也在考前比较好地做了查缺补漏。著名数学家波利亚指出：试着解决一个容易着手的简单问题、特殊的问题、类似的问题。卷子多了，时间少了，自然需要对卷子、对题目做出筛选，在复习的时候做到举一反三，渗透思想方法尤为重要，基于对平时所学知识的拓展和延伸，无论在学习能力和解题能力上，再上一个台阶。本文即选取一道质检题为载体，充分发挥学生主观能动性，并适时交流，如何巧思构造，妙解题型。

一、回顾试题

如图1，在矩形ABCD 中，对角线AC、BD 相交于点O，E 是边AD 的中点，且DC=1。

（1）求证：AB=DE；

（2）求tan ∠EBD 的值。学生刚参加完市质检，对题目的熟悉度较高，热情度较高，本题立足基本求线段长度的方法，构造直角三角形求锐角三角函数。适合用来复习巩固与提高。

二、展示问题（2）各种解法

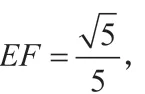
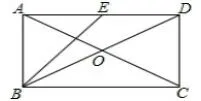
图1

作高构造直角三角形，有高的地方可想起用面积法，面积法可求出所需条件EF 的长。

解法二：如图3，过点D 作DF ⊥BE 的延长线于点F，与解法一同理，利用△BDE面积求出DF，利用勾股定理求出即可求出的值。

图2

高不一定作在三角形内部，钝角三角形的高亦可作在外部，学生能想到此法，应给予充分肯定，善于利用高构造面积法。解法充分体现了面积法的一个基本技巧，即用两种或两种以上的方法表示同一个图形的面积，进而通过面积等式找出所求量之间的关系，或求出需要的量。

解法三：如图4，连接CE 交BD 于点F，易证△BCE 是等腰直角三角形，∠BEF=90°，由勾股定理求出CE，由△DEF ∽△BCF 可求出EF，即可求出的值。

图3

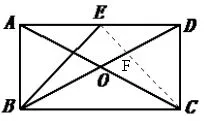
图4

直角三角形是最常见的三角形，在历年中考题中都有直角三角形的身影，最常见的可数直角三角形三角函数的实际应用。有些是明显存在直角三角形，有些是根据已知条件隐藏着直角三角形，只需简单作辅助线。

利用现有图形特征，直接连接EC，构造等腰直角三角形，利用相似，此法辅助线简单，善于观察，充分利用已知条件。

和角公式作为初中数学知识的课外补充，学生在理解公式由来基础上，能用公式求角度正切值，不需要作辅助线，为高中学习奠定基础。

解法五：如图5，以点B 为原点，边BC 所在直线为x 轴建立平面直角坐标系，可知点E、B、D 的坐标，求出直线BD 的函数关系式，利用点到直线距离公式求出点E 到直线BD 的距离EF，图5勾股定理求出BF，即可求出的值。

图5

建立平面直角坐标系，并非对每道几何题都适用、好用，但有了此种思维方式，在需要的时候，可以达到优化解题目的。

各种解法展示，让学生体验不同方法，发散思维，多角度解题思路，增强自主归纳能力。

以上方法均为构造直角三角形，同学们是否可以考虑转化锐角∠EBD，将它转化到一个直角三角形中来求正切值呢？

引导：∠EBD 可以看作是定线段DE 所对的张角，定线段DE 是否可以对其他与之相等的张角呢？

生：可以构造圆。利用“在同圆或等圆中，同弧所对的圆周角相等，都等于所对圆心角的一半”。

如图6，可以将∠EBD 转化到∠EFD，而∠EFD=90°，△DEF 是直角三角形。

换角度思考，不一定只局限于构造直角三角形，可以利用定线段所对张角相等，通过构造辅助圆把角转化。

三、拓展提高

问 题（3）：如 图6，以 点B 为 原点，边BC 所在直线为x 轴建立平面直角坐标系，在坐标轴上是否存在点M，使得tan ∠DME 与（2）中求得的值相等？若存在，请求出点M 的坐标，若不存在，请说明理由。

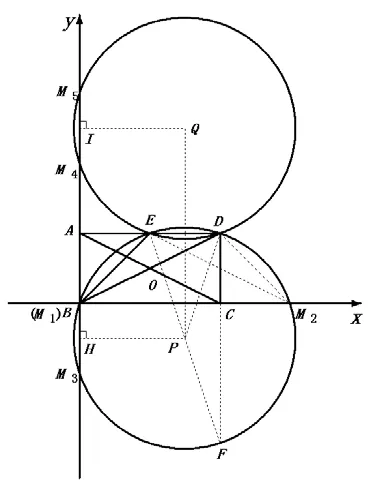
图6

角是几何图形中最重要的元素，而圆的特征赋予角极强的活性，使得角能灵活地互相转化。根据圆心角与圆周角的倍半关系，可实现圆心角与圆周角的转化；由同弧或等弧所对的圆周角相等，可将圆周角在大小不变的情况下，改变顶点在圆上的位置进行探索；由圆内接四边形的对角互补和外角等于内对角，可将与圆有关的角互相联系起来。

转化角在此类问题中，能起到化隐为显、化难为易的解题效果。不仅可以构造直角三角形来求锐角三角函数，还可以构造辅助圆，利用“在同圆或等圆中，同弧所对的圆周角相等，都等于所对圆心角的一半”，将锐角转化，达到化难为易的解题效果。

构造辅助圆巧解中考压轴题关于动点对定线段所张的角为定值问题，从表面看似与圆无关，但如果我们能深入挖掘题目中的隐含条件，善于联想所学定理，巧妙地构造符合题意特征的辅助圆，再利用圆的有关性质来解决问题，往往能起到化隐为显、化难为易的解题效果，还考查了学生的创造性思维，有利于培养学生分析问题的能力。这里，构造辅助圆实则成了解题的关键。